膨胀卷积空洞卷积Dilated Convolution

膨胀卷积，也叫空洞卷积，Dilated Convolution，也有叫 扩张卷积；

空洞卷积 是 2016在ICLR(International Conference on Learning Representation)上被提出的，本身用在图像分割领域，被deepmind拿来应用到语音(WaveNet)和NLP领域，它在物体检测也发挥了重要的作用，对于小物体的检测十分重要

普通卷积 

先来看看 普通卷积 

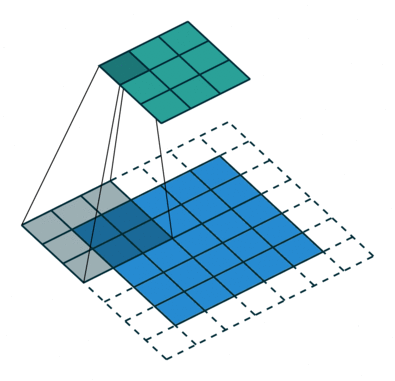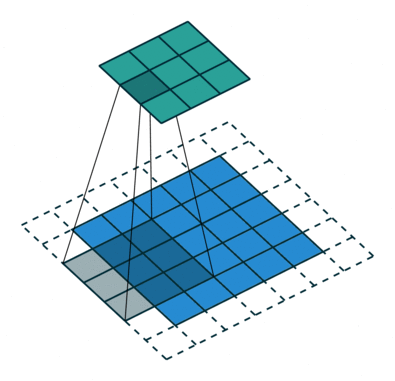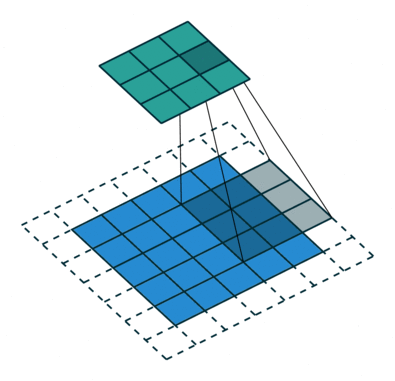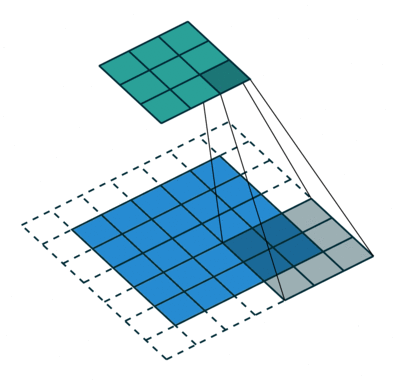
卷积后需进行池化 pooling，池化除了 降维、提升局部位移鲁棒性 等作用外，还有 增大感受野 的作用，

但是在 pooling 时，会丢失一部分信息，特别是一些 细节信息 和 小目标信息，对任务造成一定的影响：

1.在图像识别任务中，丢失细节可能降低准确率

2.在目标检测任务中，小目标检测 受影响较大

3.在语义分割任务中，下采样后的上采样无法还原这些信息

如果没有 pooling，感受野 太小，

不利于 在图像需要全局信息、语音文本需要较长的 sequence 信息依赖 等问题

感受野

卷积模块 输出结果中 一个元素 对应 输入层的 区域大小，代表 卷积核 在 图像上看到的区域大小，感受野 越大，包含的 上下文关系 越多，【通俗理解就是 视野更广阔了，看问题更全面了 等等】

空洞卷积

为了避免 pooling 的影响，提出了 空洞卷积

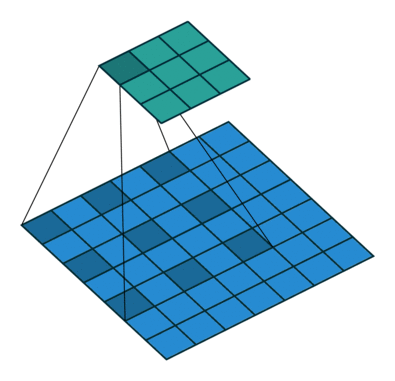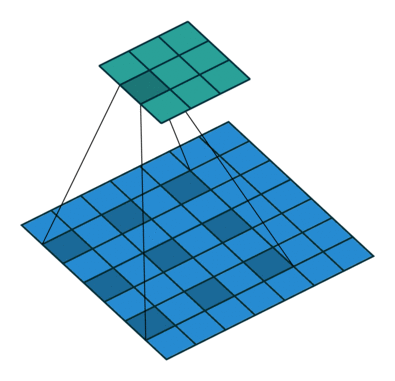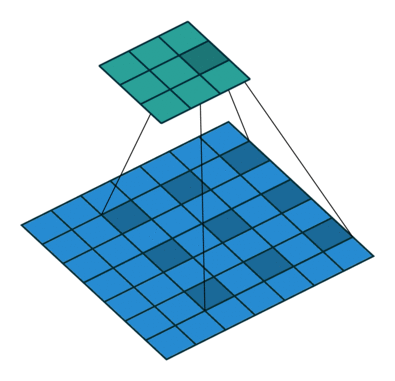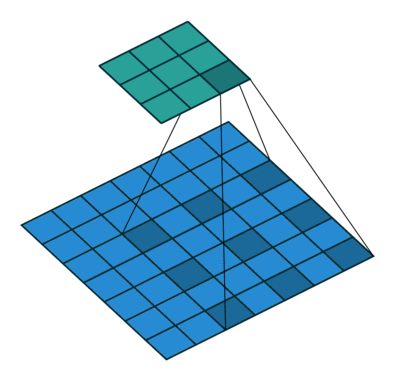
VS 普通卷积

空洞卷积其实 就是在 普通卷积核中间 插 0，看起来像中间有洞，故称空洞；

空洞卷积与 普通卷积 参数量 相同；

空洞卷积与 普通卷积 输出的 feature map 大小相同；

膨胀率 

空洞卷积中引入 膨胀率 dilation_rate 的概念，也叫 扩张率，空洞数，

膨胀率 代表 将 原来的一个 元素 扩展到 多少倍，扩展后的 卷积核尺寸 dilation_rate*（kernel_size - 1）+1，

如下图

a为 普通卷积核为 3x3，感受野 9；

b 膨胀率为 2，原先1个元素变成2个，5x5，感受野 25；

c 膨胀率为 3，原先1个元素变成3个，7x7，感受野 49；

保持数据结构不变

pooling 操作一般会改变 数据尺寸，在 图像分割 领域，下采样后需上采样，数据尺寸会发生变化，而空洞卷积只有卷积，没有池化，可以保持数据结构不变

空洞卷积的问题与优化 

栅格效应 Gridding Effect

这张图代表了3层空洞卷积，每层在 原始输入 上 参与计算的 像素个数，可忽略，直接看下面的图 

多个相同膨胀率的空洞卷积堆叠

左侧从下往上看，相当于一个卷积网络，每次卷积采用 膨胀率为 2 的空洞卷积，

右侧是卷积后的统计分析，整个图代表 原始输入，每个格子代表一个像素，格子里的值代表 3次卷积后，该像素被 计算的次数，

可以看到有些 像素 是没有参与计算的，造成了大量的信息丢失，影响最终效果，

论文中称 卷积核 不连续；

多个不同膨胀率的空洞卷积堆叠

左侧膨胀率分别为 1 2 3，右侧所有像素都参与计算了，信息利用率大大增强，

同时感受野 等于 上个图，大于 下个图(普通卷积)

多个普通卷积堆叠

感受野明显小很多 

Hybrid Dilated Convolution（HDC) 

混合膨胀卷积，

空洞卷积会产生 栅格效应，需要 设计 膨胀率 使得卷积核能够覆盖所有像素，HDC 用于解决这一问题。

HDC 要求 膨胀率 满足如下要求

1.满足公式和约束

Mi 表示 第 i 层 最大 可使用 的 膨胀率，ri 表示 第 i 层的膨胀率， n 表示 膨胀卷积核  的 个数，

下面分别表示 膨胀系数 为 [1 2 5] 和 [1 2 9]

2.锯齿结构

dilated rate设计成了锯齿状结构，例如[1, 2, 5, 1, 2, 5]这样的循环结构 

锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息，大 dilation rate 来关心远距离信息)。

这样卷积依然是连续的，依然能满足VGG组观察的结论，大卷积是由小卷积的 regularisation 的 叠加。

3.公约数不能大于 1

叠加的膨胀卷积的膨胀率dilated rate不能有大于1的公约数（比如[2, 4, 8]），不然会产生栅格效应

下面代码用于 画 上面的图

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap


def dilated_conv_one_pixel(center: (int, int),
                           feature_map: np.ndarray,
                           k: int = 3,
                           r: int = 1,
                           v: int = 1):
    """
    膨胀卷积核中心在指定坐标center处时，统计哪些像素被利用到，
    并在利用到的像素位置处加上增量v
    Args:
        center: 膨胀卷积核中心的坐标
        feature_map: 记录每个像素使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
        v: 使用次数增量
    """
    assert divmod(3, 2)[1] == 1

    # left-top: (x, y)
    left_top = (center[0] - ((k - 1) // 2) * r, center[1] - ((k - 1) // 2) * r)
    for i in range(k):
        for j in range(k):
            feature_map[left_top[1] + i * r][left_top[0] + j * r] += v


def dilated_conv_all_map(dilated_map: np.ndarray,
                         k: int = 3,
                         r: int = 1):
    """
    根据输出特征矩阵中哪些像素被使用以及使用次数，
    配合膨胀卷积k和r计算输入特征矩阵哪些像素被使用以及使用次数
    Args:
        dilated_map: 记录输出特征矩阵中每个像素被使用次数的特征图
        k: 膨胀卷积核的kernel大小
        r: 膨胀卷积的dilation rate
    """
    new_map = np.zeros_like(dilated_map)
    for i in range(dilated_map.shape[0]):
        for j in range(dilated_map.shape[1]):
            if dilated_map[i][j] > 0:
                dilated_conv_one_pixel((j, i), new_map, k=k, r=r, v=dilated_map[i][j])

    return new_map


def plot_map(matrix: np.ndarray):
    plt.figure()

    c_list = ['white', 'blue', 'red']
    new_cmp = LinearSegmentedColormap.from_list('chaos', c_list)
    plt.imshow(matrix, cmap=new_cmp)

    ax = plt.gca()
    ax.set_xticks(np.arange(-0.5, matrix.shape[1], 1), minor=True)
    ax.set_yticks(np.arange(-0.5, matrix.shape[0], 1), minor=True)

    # 显示color bar
    plt.colorbar()

    # 在图中标注数量
    thresh = 5
    for x in range(matrix.shape[1]):
        for y in range(matrix.shape[0]):
            # 注意这里的matrix[y, x]不是matrix[x, y]
            info = int(matrix[y, x])
            ax.text(x, y, info,
                    verticalalignment='center',
                    horizontalalignment='center',
                    color="white" if info > thresh else "black")
    ax.grid(which='minor', color='black', linestyle='-', linewidth=1.5)
    plt.show()
    plt.close()

def main():
    # bottom to top
    dilated_rates = [1, 2, 3]
    # init feature map
    size = 31
    m = np.zeros(shape=(size, size), dtype=np.int32)
    center = size // 2
    m[center][center] = 1
    # print(m)
    # plot_map(m)

    for index, dilated_r in enumerate(dilated_rates[::-1]):
        new_map = dilated_conv_all_map(m, r=dilated_r)
        m = new_map
    print(m)
    plot_map(m)

if __name__ == '__main__':
    main()

参考资料：

https://www.cnblogs.com/pinking/p/9192546.html　　膨胀卷积与IDCNN              　　　　　　　　言简意赅，有图 有代码，适合入门

https://www.bilibili.com/video/BV1Bf4y1g7j8?spm_id_from=333.337.search-card.all.click　　　　　b站视频，讲得很清楚，特别是 gridding effect 问题 及 HDC 策略

https://blog.51cto.com/u_15072927/4308099　　　　　　　　　　　　　　　　　　　　　　　　基本和 上个视频对应，建议先看视频再看该文章

https://blog.csdn.net/qq_27586341/article/details/103131674　　膨胀卷积（Dilated convolution）

https://blog.csdn.net/qq_35495233/article/details/86638098　　NLP进阶之（七）膨胀卷积神经网络

https://zhuanlan.zhihu.com/p/113285797　　吃透空洞卷积(Dilated Convolutions)

https://www.zhihu.com/question/54149221/answer/1683243773　　如何理解空洞卷积（dilated convolution）？

https://zhuanlan.zhihu.com/p/89425228　　空洞（扩张）卷积（Dilated/Atrous Convolution）