粒子群算法 PSO【1】- 基本原理

算法简介

粒子群算法，Particle Swarm optimization，简称PSO，是由Eberhart博士和kennedy博士发明的一种启发式算法，

其思想来源于 群体间互相协作和信息共享，使得群体行为形成从无序到有序的演化，进而达到目的 的自然现象；

通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。

通常认为它是群集智能 (Swarm intelligence, SI) 的一种。

算法原理

形象描述

粒子群算法源于鸟群觅食行为；　　【或者虫儿觅食，蜂群觅食，都差不多】

假设有一群鸟（种群），在某片森林（解空间）寻找食物 [的位置]（最优解）；

起初，鸟儿都不知道食物在哪里，各自在随意飞翔（种群初始化），

但他们有 一种超能力据说是嗅觉 能判断自己离食物的距离，并且能记录自己在飞行过程中离食物最近时的位置（个人经验）；　　【位置对应解，距离代表适应度/目标函数】

同时，鸟群有个特异功能，类似有个微信群，能够得知其他鸟经过的离食物最近的位置（群体经验）；

鸟儿为了得到食物必须做出决策：在当前位置和速度状态下，下一步应该往哪飞呢？（更新解）

实际上，鸟儿会结合自己的经验和群体经验做出最终决策；　　【决策是下一步的速度，包括大小和方向，更新解更新的是位置】

然后重复以上过程，即可找到食物

数学描述

粒子群算法涉及两个最重要的公式

　　速度更新公式　　

　　　　位置更新公式

i 代表粒子编号，d 代表解维度编号；

v 代表速度，x 代表位置；

w 代表惯性因子，即当前飞行速度的惯性，

c1，c2为经验权重，c1也叫个体学习因子，c2 也叫社会学习因子，r1，r2代表折扣因子，一般取值0-1；

α 代表约束因子，控制速度的权重；

pi 代表粒子 i 的个体最优经验；

pg 代表群体最优经验；

补充说明

部分内容属于摘抄，不一定对，仅供参考

1. 越界处理：为了限制某个粒子的飞翔范围过大，我们为粒子的每一个维度设置一个最大飞翔速度Vmax，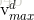

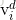
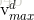
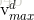
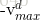
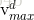
如果粒子i在d维上的飞翔速度大于Vmax，则将这一维上的飞翔速度设置为Vmax，如果小于-Vmax,则将其设置为-Vmax。

Vmax的取值一般为对应维度所代表的决策变量取值范围的百分之十到百分之二十。即 0.2*(Vmax-Vmin)。 

2. 惯性因子：用来控制继承多少粒子当前的速度的，越大则对于当前速度的继承程度越小，越小则对于当前速度的继承程度越大。有些同学可能会产生疑问，是不是说反了。其实不是，从公式中可以明确看出，其值越大，则速度的改变幅度就越大，则对于粒子的当前速度继承越小；反之，速度的改变幅度越小，则对于粒子当前速度继承越大。

因此值越大，则解的搜索范围越大，可以提高算法的全局搜索能力，但也损失了局部搜索能力，有可能错失最优解；

反之值越小，则解的搜索范围也就越小，算法的全局搜索能力也就越小，容易陷入局部最优。

如果是变量，则其值应该随着迭代次数的增加而减小（类似于梯度下降当中的学习率）。如果为定值，则建议在0.6到0.75之间进行选取。

3. 加速常数c1、c2：加速常数控制着速度的计算是更加看重自身经验还是群体经验。取值在学术界分歧很大主要有如下几种情况：

学者	c1和c2
Clerc	c1=c2=2.05
Carlisle	c1=2.8,c2=1.3
Trelea	w=0.6,c1=c2=1.7
Eberhart	w=0.729,c1=c2=1.494

 

算法步骤

注意对迭代过程中不可行解的处理　　　　【可参考我的遗传算法相关博客】

1. 惩罚

2. 人工修复

示例代码

'''
以一个简单的例子来介绍算法的流程。
假设我们需要寻找函数 y=x1^2+x2^2+x3^3+x4^4 在[1,30]之间的最大值。
我们很容易就知道，当x1=x2=x3=x4=30时，该函数能取到最大值。
'''

import random
import numpy as np
import matplotlib.pyplot as plt


class PSO:
    def __init__(self, NGEN, popsize, low, up):
        # 初始化
        self.NGEN = NGEN  # 迭代的代数
        self.pop_size = popsize  # 种群大小
        self.var_num = len(low)  # 变量维度
        self.bound = [low, up]

        # 初始化第0代初始全局最优解
        # self.pop_x = np.random.uniform(low, up, size=(self.pop_size, self.var_num))  # 所有粒子的位置
        # self.pop_x = np.random.randint(low, up, size=(self.pop_size, self.var_num))
        self.pop_x = np.random.randint(12, 21, size=(self.pop_size, self.var_num))
        print(self.pop_x)
        self.pop_v = np.random.rand(self.pop_size, self.var_num)  # 所有粒子的速度
        # print(self.pop_v)
        self.p_best = self.pop_x  # 每个粒子最优的位置
        temp = -1
        for i in range(self.pop_size):
            fit = self.fitness(self.p_best[i])
            if fit > temp:
                self.g_best = self.p_best[i]
                temp = fit

    def fitness(self, ind_var):
        """
        个体适应值计算
        """
        x1, x2, x3, x4 = ind_var
        y = x1 ** 2 + x2 ** 2 + x3 ** 3 + x4 ** 4
        return y

    def update_operator(self, pop_size):
        """
        更新算子：更新下一时刻的位置和速度
        """
        c1 = 0.8  # 学习因子，一般为2
        c2 = 0.99
        w = 0.4  # 自身权重因子
        for i in range(pop_size):
            # 更新速度
            self.pop_v[i] = w * self.pop_v[i] + 
                            c1 * random.uniform(0, 1) * (self.p_best[i] - self.pop_x[i]) + 
                            c2 * random.uniform(0, 1) * (self.g_best - self.pop_x[i])
            # 更新位置
            self.pop_x[i] = self.pop_x[i] + self.pop_v[i]

            # 越界保护  -- 不可行解的人工修复
            for j in range(self.var_num):
                if self.pop_x[i][j] < self.bound[0][j]:
                    self.pop_x[i][j] = self.bound[0][j]
                if self.pop_x[i][j] > self.bound[1][j]:
                    self.pop_x[i][j] = self.bound[1][j]

            # 更新p_best和g_best
            fit_x = self.fitness(self.pop_x[i])
            if fit_x > self.fitness(self.p_best[i]):  # 个体最优
                self.p_best[i] = self.pop_x[i]
            if fit_x > self.fitness(self.g_best):     # 群体最优
                self.g_best = self.pop_x[i]

    def main(self):
        popobj = []             # 记录全局最优粒子的适应度
        self.ng_best = np.zeros((1, self.var_num))[0]     # 记录全局最优粒子
        print(self.ng_best)
        for gen in range(self.NGEN):
            self.update_operator(self.pop_size)
            popobj.append(self.fitness(self.g_best))
            print('############ Generation {} ############'.format(str(gen + 1)))
            if self.fitness(self.g_best) > self.fitness(self.ng_best):
                self.ng_best = self.g_best.copy()
            print('最好的位置：{}'.format(self.ng_best))
            print('最大的函数值：{}'.format(self.fitness(self.ng_best)))
        print("---- End of (successful) Searching ----")

        plt.figure()
        plt.title("Figure1")
        plt.xlabel("iterators", size=14)
        plt.ylabel("fitness", size=14)
        plt.plot(range(self.NGEN), popobj, color='b', linewidth=2)
        plt.show()


if __name__ == '__main__':
    NGEN = 500
    popsize = 100
    low = [1, 10, 1, 1]
    up = [30, 50, 30, 30]
    pso = PSO(NGEN, popsize, low, up)
    pso.main()

参考资料：

https://blog.csdn.net/yy2050645/article/details/80740641　　粒子群算法

https://www.zhihu.com/question/23103725/answer/365298309　　如何直观形象地理解粒子群算法？

https://www.cnblogs.com/yncxzdy/p/4280207.html　　标准粒子群算法（PSO）

https://finthon.com/python-pso/　　Python手把手构建粒子群算法（PSO）实现最优化搜索

https://www.jb51.net/article/128113.htm　　Python编程实现粒子群算法(PSO)详解