最近做了不少的组合数的题
这里简单总结一下下
1.n,m很大p很小 且p为素数
p要1e7以下的 可以接受On的时间和空间
然后预处理阶乘 Lucas定理来做
以下是代码

/*Hdu3037 Saving Beans*/ #include<cstdio> #include<cstring> #include<iostream> #define ll long long #define maxn 1000010 using namespace std; ll T,n,m,p,f[maxn]; void Get(){ f[0]=1; for(int i=1;i<=p;i++) f[i]=f[i-1]*i%p; } ll qm(ll a,ll b){ a%=p;ll r=1; while(b){ if(b&1)r=r*a%p; b>>=1;a=a*a%p; } return r; } ll C(ll a,ll b){ if(b>a)return 0; return f[a]*qm(f[b]*f[a-b],p-2)%p; } ll Lcs(ll a,ll b){ if(b==0)return 1; return C(a%p,b%p)*Lcs(a/p,b/p)%p; } int main(){ cin>>T; while(T--){ cin>>n>>m>>p;Get(); cout<<Lcs(n+m,n)<<endl; } return 0; }
2.n很大,m很小,p很大,且p为素数p>m
m很小我们可以直接暴力,保证了p大于m,也就是pm互质,保证存在逆元

/*[FZU 2020] 组合*/ #include<cstdio> #include<cstring> #include<iostream> #define ll long long #define maxn 1000010 using namespace std; ll T,n,m,p; ll qm(ll a,ll b){ a%=p;ll r=1; while(b){ if(b&1)r=r*a%p; b>>=1;a=a*a%p; } return r; } ll C(ll a,ll b){ if(b>a)return 0;ll res=1; for(ll i=a,j=1;j<=b;i--,j++){ res*=i%p;res%=p;res*=qm(j,p-2);res%=p; } return res; } int main(){ cin>>T; while(T--){ cin>>n>>m>>p; cout<<C(n,m)<<endl; } return 0; }
3.n很大,m很小,p很大,且p为素数
同上可用暴力,但是p虽然会prime但是可能m是p的倍数逆元可能不存在
所以我们用Lucas定理,把m分解成一个p进制数,保证比p小,就可以同上了

/*ZOJ 3557 How Many Sets II */ #include<cstdio> #include<cstring> #include<iostream> #define ll long long using namespace std; ll T,n,m,p; ll qm(ll a,ll b){ a%=p;ll r=1; while(b){ if(b&1)r=r*a%p; b>>=1;a=a*a%p; } return r; } ll C(ll a,ll b){ if(b>a)return 0;ll res=1; for(ll i=a,j=1;j<=b;i--,j++){ res*=i%p;res%=p;res*=qm(j,p-2);res%=p; } return res; } ll Lcs(ll a,ll b){ if(b==0)return 1; return C(a%p,b%p)*Lcs(a/p,b/p)%p; } int main(){ while(cin>>n>>m>>p) cout<<Lcs(n-m+1,m)<<endl; return 0; }
下面是几个性质
1.C(n,0),C(n,1),,,,,C(n,n)里面奇数的个数
= 2^(n二进制表示下的1的个数) (好像有组合数的做法,这个是打表找的规律)
2.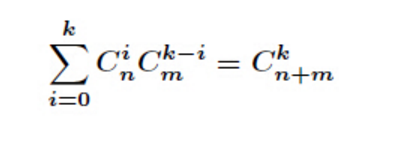
范德莫恒等式
错排问题&&容斥原理
Ai表示i在i位置的序列个数,显然 Ai=(n-1)! Ai∩Aj=(n-2)!
Ai的反也就是i不在i位置的序列个数,
所以A1反∩A2反∩.....∩An反 = ( A1∪A2∪....∪An )反=U- ( A1∪A2∪....∪An )
U=n!,所以ans=n!-C(n,1)*(n-1)!+C(n,2)*(n-2)!......
代码

#include<cstdio> #include<cstring> #include<iostream> #define ll long long using namespace std; int n;ll f[25],ans; int main(){ f[1]=1;for(int i=2;i<=20;i++)f[i]=f[i-1]*i; while(~scanf("%d",&n)){ ans=f[n];for(int i=1;i<=n;i++) if(i&1)ans-=f[n]/f[i]; else ans+=f[n]/f[i]; printf("%lld ",ans); } return 0; }
这个是比较裸地,然后我们看一个题目
HDU 2068
题意:满足a[i]=i的个数一般或以上的序列个数
我们就枚举有x个a[i]=i,然后剩下的就是n-x错排了 乘法原理乘一下
高中用的为数不多的组合数的题目就是隔板法,还有一种模型就是解的个数
x1+x2+x3....+xm=n 问合法的x1x2x3....个数,若保证是正整数就是C(n-1,m-1),可能为0 那就每个x都加一 右边变成n+m,答案就是C(n+m-1,m-1)
题意:x1+x2+x3....+xm=k 0<=xi<=n
先不管<=n这个条件,我们先转化成正整数:x1+x2+x3....+xm=k+m
考虑<=n这件事: 我们能求出来的是没有上界的模型,倘若我们知道只有x1>n,那我们用x1-n替换x1,就把这个变成了我们可以解决的模型(注意右边-n)
然后就可以想到容斥原理,就是看有几个xi>n,我们剪掉一个x大于n的时候会多剪掉两个的,就是简单的+-+-的容斥模型了
然后注意特殊的数据

#include<cstdio> #define ll long long using namespace std; int T,n,m,k; const ll mod=998244353; ll ans,f[200010],inv[200010]; void extgcd(ll a,ll b,ll& d,ll& x,ll& y){ if(!b){ d=a;x=1;y=0; } else{ extgcd(b,a%b,d,y,x); y-=x*(a/b); } } ll inverse(ll a,ll n){ ll d,x,y; extgcd(a,n,d,x,y); return d==1?(x+n)%n:0; } ll C(int x,int y){ return f[x]*inv[y]%mod*inv[x-y]%mod; } int main(){ scanf("%d",&T);f[0]=1;inv[0]=1; for(int i=1;i<=200000;i++){ f[i]=f[i-1]*i%mod; inv[i]=inverse(f[i],mod); } while(T--){ scanf("%d%d%d",&n,&m,&k); if((n-1)*(ll)m<k){ printf("0 ");continue; } int x=k-1+m,y=m-1;ans=0;f[0]=0; for(int i=1;i<=m&&x>=y;i++,x-=n){ if(i&1)ans+=C(m,i-1)*C(x,y)%mod; else ans-=C(m,i-1)*C(x,y)%mod; ans+=mod;ans%=mod; } printf("%lld ",ans); } return 0; }
再看个稍微麻烦一点的
cf451E
题意同上,只不过上界不是固定的n,是一个ai
乍一看好像挺难得因为上面的状态的是 几个不合法的, 而现在是 哪几个不合法的
不过好在m很小,我们可以利用状丫确定状态,然后容斥的时候就不能 x个不合法的一起算了
而是奇数个不合法的话,就对答案贡献为-,偶数为正.

#include<iostream> #define ll long long using namespace std; const ll mod=1000000007; int n,cnt; ll f[25],ans,s,k; void extgcd(ll a,ll b,ll& d,ll& x,ll& y){ if(!b){ d=a;x=1;y=0; } else{ extgcd(b,a%b,d,y,x); y-=x*(a/b); } } ll inverse(ll a,ll n){ ll d,x,y; extgcd(a,n,d,x,y); return d==1?(x+n)%n:0; } ll C(ll x,ll y){ ll res=1; for(ll i=x,j=1;j<=y;i--,j++){ res*=i%mod;res%=mod;res*=inverse(j,mod);res%=mod; } return res; } int main(){ cin>>n>>s; for(int i=1;i<=n;i++) cin>>f[i]; for(int S=0;S<(1<<n);S++){ cnt=0;k=s; for(int j=1;j<=n;j++) if(S&(1<<j-1)){ cnt++;k-=f[j]+1; } if(k<0)continue; if(cnt&1)ans-=C(k+n-1,n-1); else ans+=C(k+n-1,n-1); ans+=mod;ans%=mod; } cout<<ans<<endl; return 0; }
然后是一个比较emmmmm好像也不是很简单的容斥原理
UVAlive 5846
题意:一个圈上有很多点,两两连边,每条边是红/蓝,然后问形成的同色三角形的个数
ans=总三角形的个数-异色三角形的个数
tot=C(n,3),下面考虑异色三角形个数
以为只有两种颜色,所以异色三角形的构成是112或者 122
也就是说,有两个顶点连出去的边异色,我们转而研究点,对于每个点,选两条异色边,就一定构成一个异色三角形
然后每个三角形统计了两边,在/2就好了

#include<cstdio> #include<cstring> #include<iostream> #define maxn 1010 using namespace std; int T,n,a[maxn],b[maxn]; long long ans; int main(){ scanf("%d",&T); while(T--){ memset(a,0,sizeof(a)); memset(b,0,sizeof(b)); scanf("%d",&n);int x;ans=0; for(int i=1;i<n;i++) for(int j=1;j<=n-i;j++){ scanf("%d",&x); if(x)a[i]++,a[i+j]++; else b[i]++,b[i+j]++; } for(int i=1;i<=n;i++) ans-=a[i]*b[i]; ans/=2;ans+=(long long)n*(n-1)*(n-2)/6; printf("%lld ",ans); } return 0; }
