Information Theory is one of the most popular courses in Marjar University. In this course, there is an important chapter about information entropy.
Entropy is the average amount of information contained in each message received. Here, a message stands for an event, or a sample or a character drawn from a distribution or a data stream. Entropy thus characterizes our uncertainty about our source of information. The source is also characterized by the probability distribution of the samples drawn from it. The idea here is that the less likely an event is, the more information it provides when it occurs.
Generally, "entropy" stands for "disorder" or uncertainty. The entropy we talk about here was introduced by Claude E. Shannon in his 1948 paper "A Mathematical Theory of Communication". We also call it Shannon entropy or information entropy to distinguish from other occurrences of the term, which appears in various parts of physics in different forms.
Named after Boltzmann's H-theorem, Shannon defined the entropy Η (Greek letter Η, η) of a discrete random variableX with possible values {x1, x2, ..., xn} and probability mass functionP(X) as:
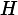

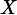














Here E is the expected value operator. When taken from a finite sample, the entropy can explicitly be written as
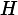




















Where b is the base of the logarithm used. Common values of b are 2, Euler's numbere, and 10. The unit of entropy is bit for b = 2, nat for b = e, and dit (or digit) for b = 10 respectively.
In the case of P(xi) = 0 for some i, the value of the corresponding summand 0 logb(0) is taken to be a well-known limit:
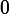

















Your task is to calculate the entropy of a finite sample with N values.
Input
There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:
The first line contains an integer N (1 <= N <= 100) and a stringS. The string S is one of "bit", "nat" or "dit", indicating the unit of entropy.
In the next line, there are N non-negative integers P1,P2, .., PN. Pi means the probability of thei-th value in percentage and the sum of Pi will be 100.
Output
For each test case, output the entropy in the corresponding unit.
Any solution with a relative or absolute error of at most 10-8 will be accepted.
Sample Input
3 3 bit 25 25 50 7 nat 1 2 4 8 16 32 37 10 dit 10 10 10 10 10 10 10 10 10 10
Sample Output
1.500000000000 1.480810832465 1.000000000000
题意:给你N个数和一个字符串str。若str为bit。则计算sigma( - log2a[i])(1 <= i <= N); str为nat时,计算sigma(- loga[i])(1 <= i <= N); str为dit时,计算sigma(- log10a[i])(1 <= i <= N)。
AC代码:
#include <cstdio> #include <cstring> #include <cmath> #include <cstdlib> #include <vector> #include <queue> #include <stack> #include <algorithm> #define LL long long #define INF 0x3f3f3f3f #define MAXN 1000 #define MAXM 100000 using namespace std; int main() { int t; int N; char str[10]; double a[110]; scanf("%d", &t); while(t--) { scanf("%d%s", &N, str); double sum = 0; for(int i = 0; i < N; i++) scanf("%lf", &a[i]), sum += a[i]; double ans = 0; if(strcmp(str, "bit") == 0) { for(int i = 0; i < N; i++) { if(a[i] == 0) continue; ans += -log2(a[i] / sum) * (a[i] / sum); } } else if(strcmp(str, "nat") == 0) { for(int i = 0; i < N; i++) { if(a[i] == 0) continue; ans += -log(a[i] / sum) * (a[i] / sum); } } else { for(int i = 0; i < N; i++) { if(a[i] == 0) continue; ans += -log10(a[i] / sum) * (a[i] / sum); } } printf("%.12lf ", ans); } return 0; }