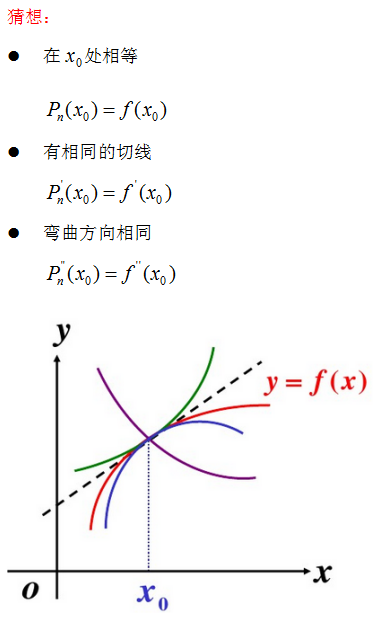
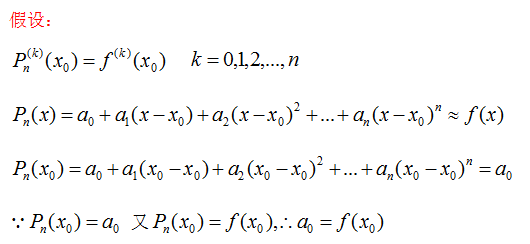


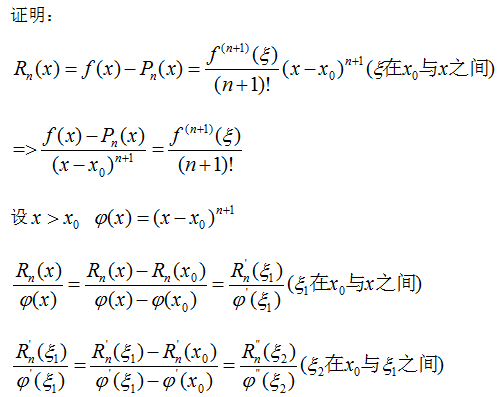
如此,用n+1次柯西定理,得:
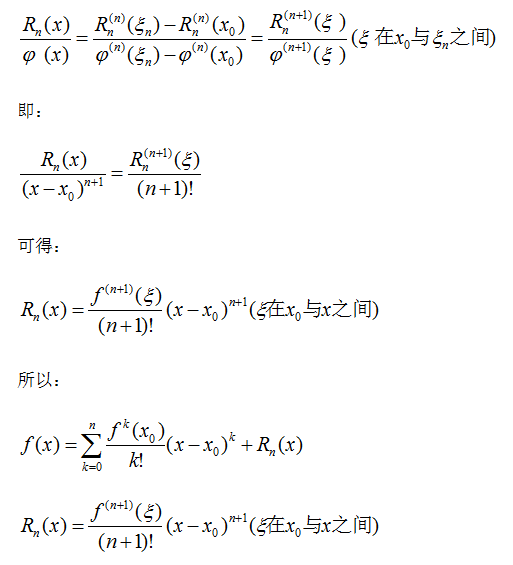
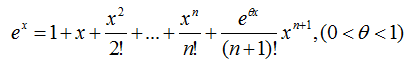
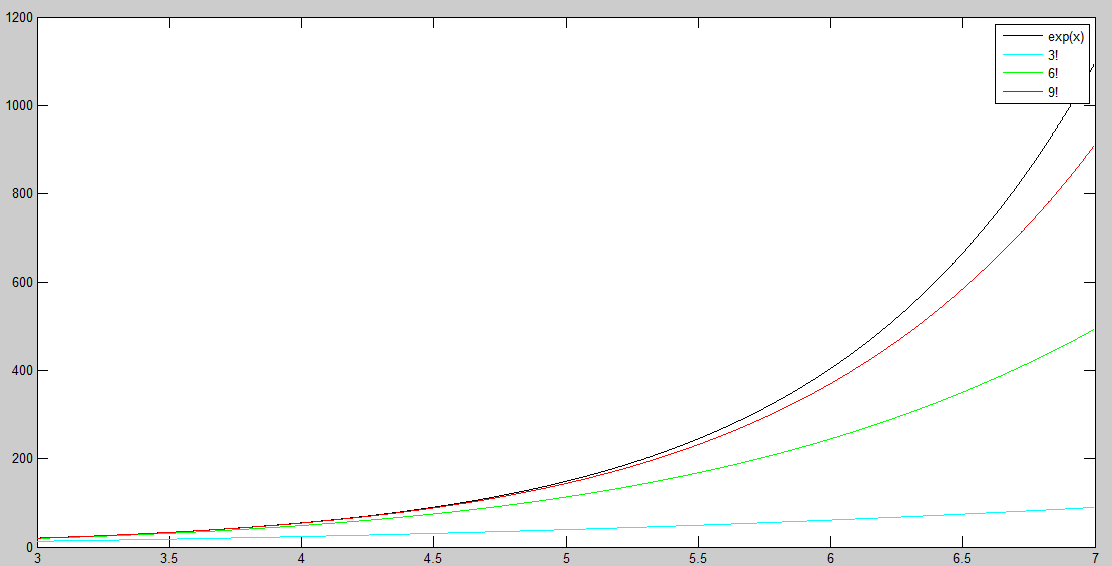
clear;clc;
syms x
ex=exp(x);
f3=1+x+x^2/2+x^3/6;
f6=1+x+x^2/2+x^3/6+x^4/24++x^5/120++x^6/720;
f9=1+x+x^2/2+x^3/6+x^4/24++x^5/120++x^6/720+x^7/5040++x^8/40320++x^9/362880;
%%%%%%%%对syms变量画图%%%%%%%
left = 3;%区间左边
size = 0.001;%步长 精度
right= 7;%区间右边
up = 50;
down = 10;
%axis([XMIN XMAX YMIN YMAX]) 设置二维图的x-y坐标范围
t=[left:size:right-size];
z=subs(ex,x,t);
plot(t,z,'k');
hold on
t=[left:size:right-size];
z=subs(f3,x,t);
plot(t,z,'c');
hold on
t=[left:size:right-size];
z=subs(f6,x,t);
plot(t,z,'g');
hold on
t=[left:size:right-size];
z=subs(f9,x,t);
plot(t,z,'r');
legend('exp(x)','3!','6!','9!');
sin(x):--------------------------------------------
syms x
ex=sin(x);
f1=x;
f3=x-x^3/factorial(3);
f5=x-x^3/factorial(3)+x^5/factorial(5);
f7=x-x^3/factorial(3)+x^5/factorial(5)-x^7/factorial(7);
f9=x-x^3/factorial(3)+x^5/factorial(5)-x^7/factorial(7)+x^9/factorial(9);
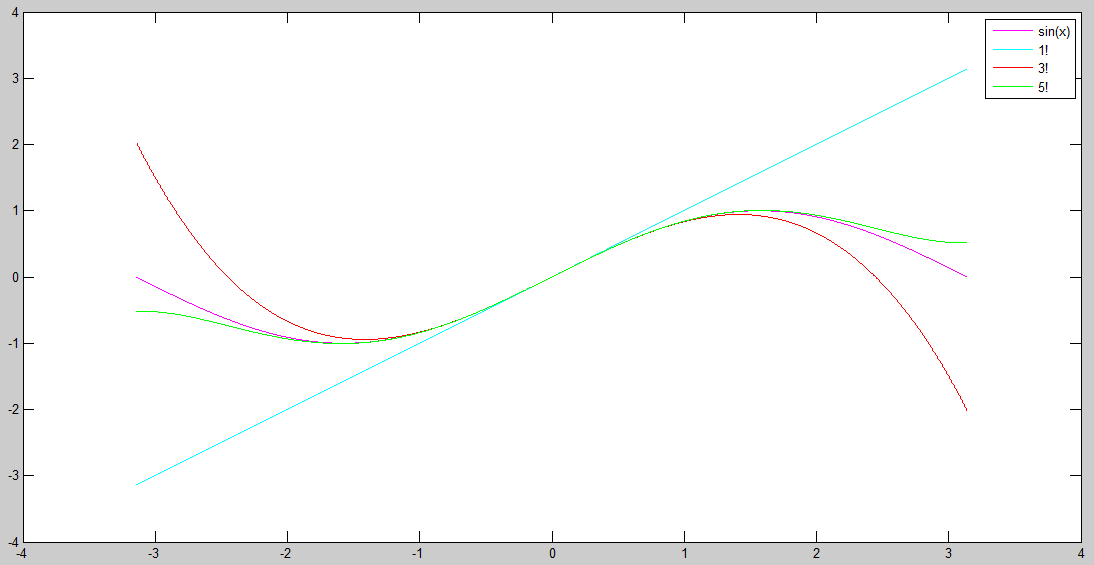
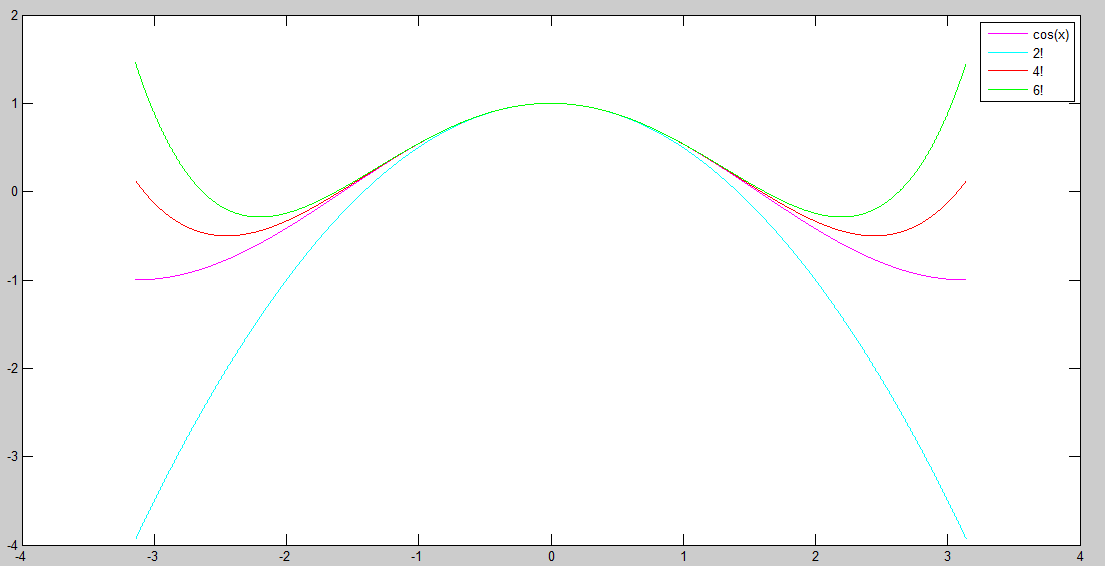
cos(x):--------------------------------------------