什么是神经网络？
神经网络由一个个的神经单元组成。包括输入层，隐藏层和输出层。神经网路的一个重要组成部分是激活函数，常见的激活函数有Sigmoid, tanh, ReLU, leaky relu, maxout, ELU 等。
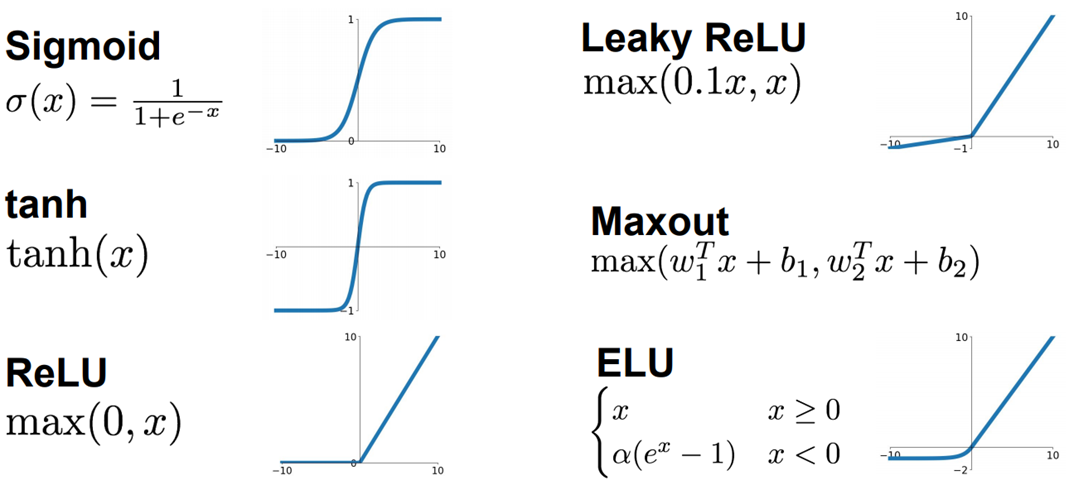
Sigmoid 激活函数的导数计算公式如下：
tanh 的导数：
ReLU在零这一点的梯度怎么计算？
下面是一个三层的全连接神经网络
一个输入层( x )，一个隐藏层(a）， 一个输出层（o)。其中，
写成向量表达式：
值得注意的是， 输出 o 是 a 的线性组合， 没有激活函数 ？ （为什么这里没有激活函数呢？）
具体理由不太清楚， 可能是因为， 希望神经网络经过隐藏层的非线性转换以后将线性不可分的输入变为线性可分的输出。
如果神经网络用于分类， 其损失函数通常为 softmax cross-entropy.
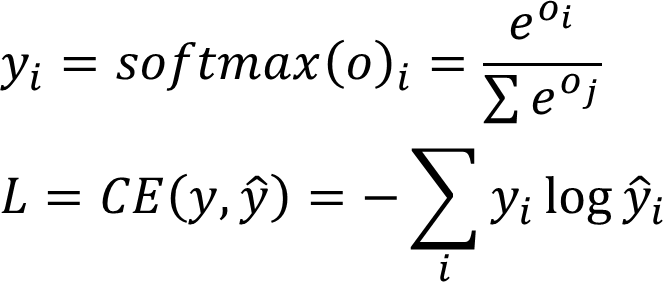对于分类问题， 损失函数通常为 Softmax Cross-Entropy， 而不是Mean Squared Error。 主要是因为SCE比MSE更容易优化。参考这篇论文。
将 Softmax 和 Cross Entropy 结合在一起， 在计算梯度的时候会得到一个很漂亮的结果。
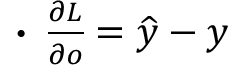
计算梯度。
首先， 复习一点关于梯度的知识。直接上图， ：）
链式法则的计算方法如下。在进行梯度计算的时候有一些技巧。两个矩阵相乘的时候， 维度对不对。 检验的时候， 看某一个元素的梯度计算公式对不对。
最后， 后面两个的梯度计算方式如下：
神经网络的一个最漂亮的数学证明， Universal Approximation Properties.
简单地说，神经网络是一个通用的函数逼近器。
