线段树

1. 背景

   假设现在有一个非常大的数组 arr，对数组里面的数字需要反复做两个操作：

       1）随机的选择一块区间，然后对区间里面的所有数字求和。

       2）随机修改数组里面的某一个值，即更新操作。

   因为数组是随机存取的，所以更新操作很容易，其时间复杂度是 $O(1)$。

   对于求和操作，其时间复杂度取决于区间的长度，假设区间长度为 $L$，则求和操作的时间复杂度为 $O(L)$。

   那有没有办法降低求和操作的时间复杂度呢？

   首先我们想到的是另外建立一个数组 sumArr，这个数组存储的是 arr 数组的前缀和，即

$$sumArr[i] = sum_{j=0}^{i}arr[j]$$

   要求某段的和，只需在 sumArr 数组里找到对应下标做一次减法操作就可以了，时间复杂度变成了 $O(1)$。

   这样做的话更新操作的时间复杂度上升了，因为每次更新 arr 数组中的一个元素，都得更新数组 sumArr。

   那有没有办法平衡一下求和和更新两个操作的时间复杂度呢？

   下面介绍线段树。

2. 线段树

   以下面数组进行举例：

       

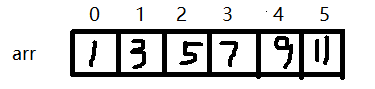
   线段树本身是一个二叉树，每个结点代表一段区间，结点值就是区间内所有元素的和。

   对于线段树中的每一个非叶子节点 $[a,b]$，它的左儿子表示的区间为 $[a,frac{a+b}{2}]$，右儿子表示的区间为 $[frac{a+b}{2}+1,b]$，

   因此线段树是平衡二叉树。

   针对上面的数组，可以建立如下线段树：

       

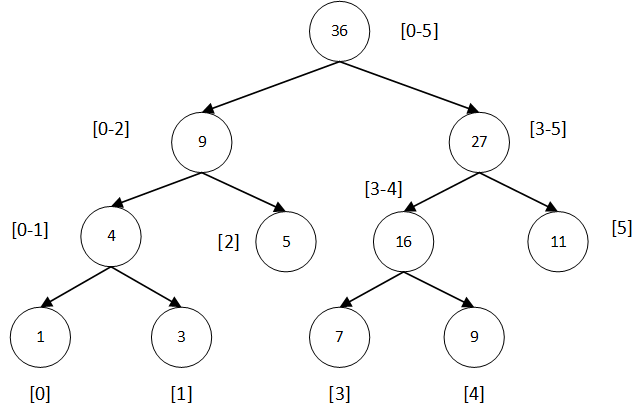
   可以看出每个叶子结点就是单个元素。

   我们将根节点标号为 0，那么对于任意一个结点 $i$，其左孩子的结点 $id$ 为 $left = 2i + 1$，右孩子的结点 $id$ 为 $right = 2i + 2$。

   因为其本身是一个平衡二叉树，所以可以用数组存储，浪费的空间小。

#include <stdio.h>

#define MAX_LEN 1000

void BuildTree(int arr[], int tree[], int node, int start, int end)
{
    if(start == end) {
        tree[node] = arr[start];
    }
    else {
        int mid = (start + end) / 2;
        int leftNode = node * 2 + 1;
        int rightNode = node * 2 + 2;

        BuildTree(arr, tree, leftNode, start, mid);
        BuildTree(arr, tree, rightNode, mid + 1, end);

        tree[node] = tree[leftNode] + tree[rightNode];
    }
}

void UpdateTree(int arr[], int tree[], int node, int start, int end, int idx, int value)
{
    if (start == end) {
        arr[idx] = value;
        tree[node] = value;
    }
    else {
        int mid = (start + end) / 2;
        int leftNode = node * 2 + 1;
        int rightNode = node * 2 + 2;

        if (idx >= start && idx <= mid) {
            UpdateTree(arr, tree, leftNode, start, mid, idx, value);
        }
        else {
            UpdateTree(arr, tree, rightNode, mid + 1, end, idx, value);
        }

        tree[node] = tree[leftNode] + tree[rightNode];
    }
}

int QueryTree(int arr[], int tree[], int node, int start, int end, int L, int R)
{
    if (R < start || L > end) return 0;
    if (start == end) return tree[node];
    if(L <= start && end <= R) return tree[node];

    int mid = (start + end) / 2;
    int leftNode = node * 2 + 1;
    int rightNode = node * 2 + 2;
    int sumLeft = QueryTree(arr, tree, leftNode, start, mid, L, R);
    int sunRight = QueryTree(arr, tree, rightNode, mid + 1, end, L, R);

    return sumLeft + sunRight;
}

int main()
{
    int arr[] = {1,3,7,9,11};
    int size = 6;
    int tree[MAX_LEN] = {0};

    BuildTree(arr, tree, 0 , 0, size - 1);

    return 0;
}