提升的概念
提升是一个机器学习技术,可以用于回归和分类问题,它每一步产生一个弱预测模型(如决策树),并加权累加到总模型中;如果每一步的弱预测模型生成都是依据损失函数的梯度方向,则称之为梯度提升(Gradient boosting)
梯度提升算法首先给定一个目标损失函数,它的定义域是所有可行的若函数集合(基函数);提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值。这种在函数域的梯度提升观点对机器学习的很多领域有深刻的影响。
提升的理论意义:如果一个问题存在弱分类器,则可以通过提升的办法得到强分类器。
提升算法:
给定输入向量X和输出变量y组成的若干训练样本(x1,y1),( x2,y2),…,( xn, yn)目标是找到近似函数![]() ,使得损失函数L(y,F(X))的损失值最小
,使得损失函数L(y,F(X))的损失值最小
L(y,F(X))的典型定义为
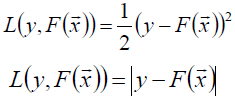
假定最优函数为![]() ,即:
,即:
![]()
绝对值中的![]() 为中位数
为中位数
假定F(x)是一组基函数fi(x)的加权和
![]()
绝对值中的![]() 为中位数的证明:
为中位数的证明:
给定样本x1,x2,...,xn,计算![]()
解:为方便推导,由于样本顺序无关,可以假定样本x1,x2,...,xn是递增排序的,则:
![]()
求偏导:
![]()
从而,前k个样本数目与后n-k个样本数目相同,即μ为中位数。
提升算法推导
梯度提升方法寻找最优解F(x),使得损失函数在训练集上的期望最小。方法如下:
首先给定常数F0(x):
![]()
以贪心的思路扩展得到Fm(x):
![]()
梯度近似:
贪心法在每次选择最优基函数f时仍然困难
1) 使用梯度下降的方法近似计算
2) 将样本带入基函数f得到f(x1), f(x2),…, f(xn)从而L退化为向量L(y1,f(x1)), L(y2,f(x2)),…, L(yn,f(xn))

上式中的权值γ为梯度下降的步长,使用线性搜索求最优步长:

初始给定模型为常数:
![]()
对于m=1到M
1) 计算伪残差 i=1,2,...,n
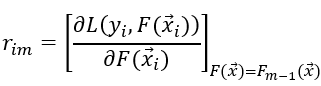
2)使用数据 ![]() 计算拟合残差的基函数fm(x)
计算拟合残差的基函数fm(x)
3)计算步长
![]()
4)更新模型
![]()
梯度提升决策树GBDT
梯度提升的点型基函数即决策树(尤其是CART)
在第m步的梯度提升是根据伪残差数据计算决策树tm(x).令tm(x)的叶结点数目为J,即树tm(x)将输入空间划分为J个不相交区域R1m,R2m,…,RJm,并且决策树tm(x)可以在每个区域中给出某个类型的确定性预测。使用指示记号I(x),对于输入x,tm(x)为:
![]()
其中,bjm是样本x在区域RJm的预测值
使用线性搜索计算学习率,最小化损失函数
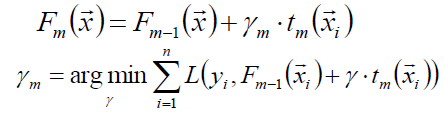
进一步:对树的每个区域分别计算步长,从而系数bjm被合并到步长中,从而:

参数设置和正则化
对训练集拟合过高会降低模型的泛化能力,需要使用正则化技术来降低过拟合
1) 对复杂模型增加惩罚项,如:模型复杂度正比于叶节点数目或者叶节点预测值的平方和等。
2) 用于决策树剪枝
- 叶结点数目控制了树的层数,一般选择4≤J≤8.
- 叶结点包含的最少样本树木
防止出现过小的叶结点,降低预测方差
梯度提升迭代次数M:
1) 增加M可降低训练集的损失值,但有过拟合风险
2) 交叉验证
衰减因子、降采样
衰减:![]()
1) v为学习率
2) v=1即为原始模型;推荐选择v<0.1的小学习率。过小的学习率会造成计算次数增多。
随机梯度提升
1) 每次迭代都对伪残差样本采用无放回的降采样,用部分样本训练基函数的参数。令训练样本数占所有伪残差样本的比例为f;f=1即为原始模型:推荐0.5≤f≤0.8。
2) 较小的f能够增强随机性,防止过拟合,并且收敛的快。
3) 降采样的额外好处是能够使用剩余样本做模型验证。
GBDT总结
1.函数估计本来被认为是在函数空间而非参数空间的数值优化问题,而阶段性的加性扩展和梯度下降手段将函数估计转换成参数估计。
2.损失函数是最小平方误差、绝对值误差等,则为回归问题;而误差函数换成多类别Logistic似然函数,则成为分类问题。
3.对目标函数分解成若干基函数的加权和,是常见的技术手段:神经网络、径向基函数、傅利叶/小波变换、SVM都可以看到它的影子。
XGBoost目标函数:J(ft)为![]()
根据Taylor展开式:
![]()
令:

得:
![]()
决策树的描述
- 使用决策树对样本做分类(回归),是从根节点到叶结点的细化过程;落在相同叶节点的样本的预测值是相同的。
- 假定某决策树的叶结点数目为T,每个叶节点的权值为
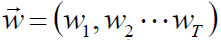 ,决策树的学习过程,就是构造如何使用特征得到划分,从而得到这些权值的过程。
,决策树的学习过程,就是构造如何使用特征得到划分,从而得到这些权值的过程。 - 样本x落在叶结点q中,定义f为:ft(x)=wq(x)
一个决策树的核心即“树结构”和“叶权值”。
正则项的定义
决策树的复杂度可考虑叶节点数和叶权值,如使用叶节点总数和叶权值平方和的加权.
![]()
目标函数计算

目标函数继续化简
![]()

XGBoost小结
相对于传统的GBDT,XGBoost使用了二阶信息,可以更快的在训练集上收敛。
由于“随机森林族”本身具备过拟合的优势,因此XGBoost仍然一定程度的具备该特性。
XGBoost实现中使用了并行/多核计算,因此训练速度快;同时它的原生语言为C/C++,这是它速度快的实践原因。
Adaboost
- 设训练数据集T={(x1,y1),( x2,y2),…,( xN, yN)}
- 初始化训练数据的权值分布
![]()
3.使用具有权值分布Dm的训练数据集学习,得到基本分类器
![]()
4.计算Gm(x)在训练数据集上的分类误差率
![]()
5.计算Gm(x)的系数
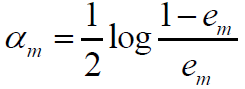
6.更新训练数据集的权值分布
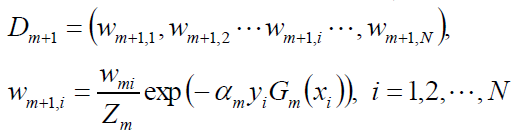
7.这里,Zm是规范化因子
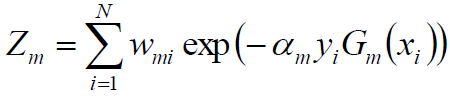
它的目的仅仅是使Dm+1成为一个概率分布
![]()
8.构建基本分类器的线性组合
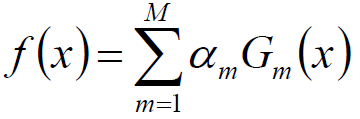
9.得到最终分类器
![]()
AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类学习方法
前向分步算法
1) 考虑加法模型
![]()
2) 其中:
a) 基函数:b(x;γm)
b) 基函数的参数γm
c) 基函数的系数βm
前向分步算法的含义
- 在给定训练数据及损失函数L(y,f(x))的条件下,学习加法模型f(x)成为经验风险极小化即损失函数极小化问题:
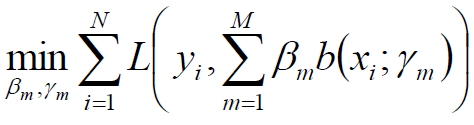
2.算法简化:如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近上式,即每步只优化损失函数:
![]()
前向分步算法的框架
输入
训练数据集T={(x1,y1),( x2,y2),…,( xn, yn)}
损失函数L(y,f(x))
基函数集{b(x;γ)}
输出:
加法模型f(x)
算法步骤:
初始化f0(x)=0
对于m=1,2,…M
极小化损失函数
![]()
得到参数βm γm
更新当前模型:
![]()
得到加法模型
![]()
前项分步算法与AdaBoost
AdaBoost算法是前向分步算法的特例,这时,模型是基本分类器组成的加法模型,损失函数是指数函数。
损失函数取:
![]()
证明
假设经过m-1轮迭代,前向分步算法已经得到fm-1(x):
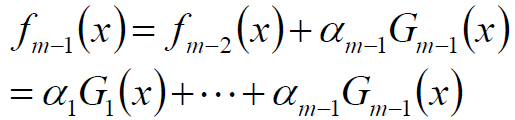
在第m轮迭代得到αm,Gm(x)和fm(x)
目标是使前向分步算法得到的αm,Gm(x)使fm(x)在训练数据集T上的指数损失最小,即

进一步
![]()
其中:
![]()
既不依赖α也不依赖G,所以与最小化无关。但 依赖于fm-1(x),所以,每轮迭代会发生变化。
基本分类器G*(x)
首先求分类器G*(x)
对于任意α>0,是上式最小的G(x)由下式得到:
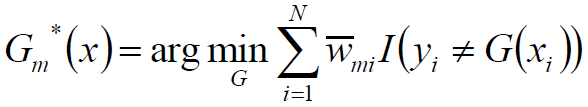
其中,
![]()
权值的计算
求权值:

将G*(x)带入:
![]()
求导得:
![]()
分类错误率为:

权值的更新
由模型:
![]()
以及权值
![]()
可以方便的得到:
![]()
权值和错误率的关键解释
1) 事实上,根据Adaboost的构造过程,权值调整公式为:
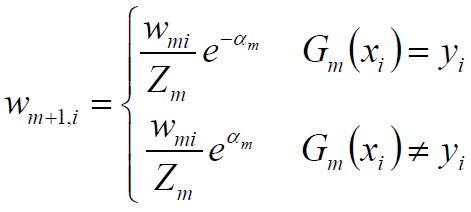
2) 二者相除得:
![]()
从而:
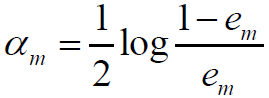
Adaboost总结
1.Adaboost算法可以看作是采用指数损失函数的提升方法,其每个基函数的学习算法为前向分布算法
2.Adaboost的训练误差是以指数速率下降的;
3.Adaboost算法不需要事先知道下界γ,具有自适应性(Adaptive),它能自适应弱分类器的训练误差率。
方差与偏差
1.Bagging能够减少训练方差,对于不剪枝的决策树、神经网络等学习器有良好的集成效果;
2.Boosting能够减少偏差,能够基于泛化能力较弱的学习器构造强学习器
除了GBDT中使用关于分类器的一阶导数进行学习之外,也可以借鉴(拟)牛顿法的思路,使用二阶导学习弱分类器。
adaboost推荐阅读https://blog.csdn.net/guyuealian/article/details/70995333
xgboost推荐阅读https://blog.csdn.net/qq_29831163/article/details/90486802