并不觉得今天学到了什么东西…感觉像上了数学课一样…
很对劲的太刀流->
一、枚举法
初二数学就有提到的。不过，有时算出的概率和直觉并不相符，所以并不能直接凭感性认识，并不对劲的人有时还得理性分析的。下面说几道不太符合直觉的题：
（1）A对B说：“我有个兄弟姐妹，你猜猜这个人和我是同性还是异性呢？”这时B猜同性还是异性更容易猜对？
听上去猜哪一个都没有区别，然而事实上并不。假设A的性别是a，与A异性是b，那么A家的孩子有这几种可能：aa,ab,ba,bb。这四种都是等可能的。但是由于A已经是a性别的了，所以bb这种组合就被排除了，只剩下ab,ba,aa这三种情况。刚刚说过它们是等可能的，也就是ab,ba,aa三种情况各占1/3的概率。这样，A的兄弟姐妹的性别是b的概率就是2/3了。
（1.5）A看B迟迟不肯回答，就又说到：“这个人比我小。”这时B该猜什么呢？
照着上一题的思路，会发现ba这一种情况被排除了，只剩下ab,aa两种等可能情况，所以B猜什么都是一样的。
也就是说，有兄弟姐妹的人可以用这个方法去坑别人了。
（2）有三扇门，其中一扇有车，另外两扇后是山羊。A知道门后的情况。A让B选一扇门，B想选到汽车。B选定了一扇门。这个A比较贪玩，故意打开了一扇B没有选、里面还是山羊的门。A问B要不要换，B该如何回答？好像是一个很经典的问题。
先分析可能会出现等可能的车-羊-羊、羊-车-羊、羊-羊-车这三种情况。假设B一开始选了第一扇门，那么对于第一种情况而言，换门肯定对他不利。而对于后两种情况而言，由于A已经打开了另一扇门后是羊的门（B肯定不会傻到换为A打开的那扇有羊的门），所以他一定会换成有车的门。这样一来，换后有车的概率是2/3。也可以这样理解：只有第一次选中时换门对B不利，第一次选中的概率是1/3，那么换门不利的概率也是1/3。这样一来，B就最好换门了。也可以夸张一些看成，A有100扇门，一扇后面是汽车，其它的后面都是山羊。在B选中后，A打开了98扇后面是山羊的门，问B要不要换成另一扇没开的门。只要B第一次没选中，换门都会使他拿到汽车。第一次没选中的概率是99/100，所以换门拿到车的概率是99/100。虽然按照平常的生活经验，做选择题时改来改去反而容易错（这不是因为蠢吗…）。
（3）B不舒服，想知道生了什么病。不幸的是，他在医院被查出【某种很重的病】。这种病的患病率是一万分之一。由于医院条件一般，有1%的概率误诊（就是一百个人中有一个有病当成没病或没病当成有病）。B仍抱有一丝侥幸心理，他想知道他患病和未患病的概率哪个更高？
听上去B已经凶多吉少了。但是本着助人为乐是精神还是给他算一算比较好。假设一共有1,000,000个人，那么其中患【某种很重的病】的有100人。可以列出以下表格：
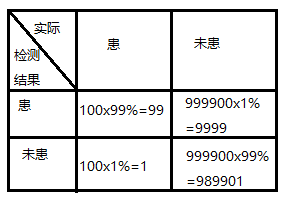
会发现被检测出患病的人中，竟然有大部分是没患病的！这样B未患病的概率就更高了。
照这么来说，是不是平时被诊断为有病了，也不用担心呢？想必不是。去医院的人大多是不舒服，更有可能是患病了。而且医院的误诊率也比本题中低多了。
（3.5）遗憾的是，B确实得了【某种很重的病】。A推荐了两家医院：甲医院致死率有10%，乙医院致死率有1%。B要不要问些别的信息再作决定？
反例：
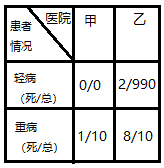
这时得了重病的B最好还是不要去乙医院。
（4）A有一个不透明袋子里有3个红球，2个白球。这些球质量、材料、形状、大小都完全一样。B先摸出一个球，再放回去，再摸出一个球。这两次摸出的红球个数的期望E(X)是多少？如果不把第一次摸出的球放回去，这两次摸出的红球个数的期望E(Y)是多少？
此时最好冷静地列表枚举摸出红球的个数：
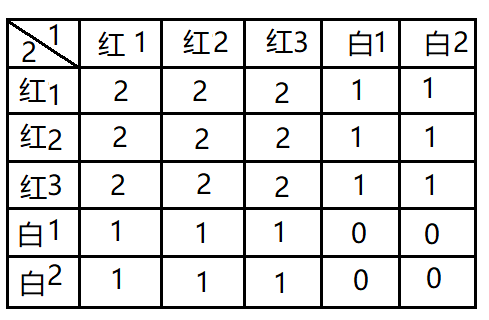
这样就可以得出E(X)=(9/25)*2+(12/25)*1+(4/25)*0=1.2。
对于不放回的情况，也可以列表：
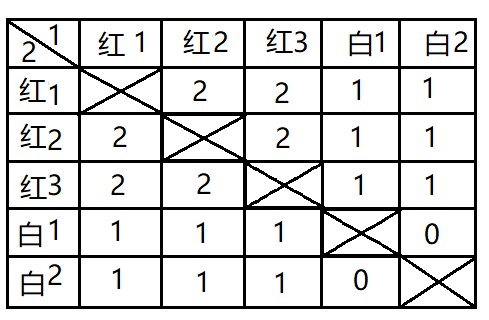
也就能得出E(Y)=(6/20)*2+(12/20)*1+(2/20)*0=1.2。
神奇的事是，E(X)=E(Y)=1.2！这个1.2有什么神奇的?想必是2*(红球数/总球数)吧。
脑筋急转弯结束了，下面进入正题。
二、全概率、全期望公式及其用法
先上公式：全概率公式：P(B)=ΣP(B|Ai)*P(Ai)；全期望公式：E(X)=ΣE(X|Ai)*P(Ai)；（X|A表示在A的条件下发生X的概率，所有Ai两两互不相容且其和为全集）
主要用法是根据这个列方程或者递推式。下面来看几道例题：
（1） A将B放进了一个房间里，这个房间有编号分别为1、2、3的三扇门和一个天窗。其中1号门通向的通道走10分钟后会走到外面，2号门通向的通道走3分钟会从天窗掉回房间，3号门通向的通道走3分钟也会从天花板掉回房间。B比较蠢，他不会走天窗，也不知道上一次走了什么门，所以每次只能随机在三扇门中选一扇走了。问B期望几分钟能走出去？
用枚举法会发现走来走去会很乱，难以枚举。但是可以这样想：每次B有1/3的概率在10分钟后出去，有1/3的概率在3分钟后回到原状态，有1/3的概率在5分钟后回到原状态。套用全期望公式，就可以列出这样的式子：E(X)=10*(1/3)+(E(X)+3)*(1/3)+(E(X)+5)*(1/3)。最终解得E(X)=18。刚好是3+5+10，是巧合吗？
（2）B喝醉了，站在悬崖的边缘，他再走一步就会掉下去。他有1/2的概率向前走，有1/2的概率后退。A站在离悬崖10步远的地方，但是他比较懒，所以只有当B走到A的位置时A才会将B带离悬崖。问B成功被A救的概率时多少？
和上一题类似地，考虑状态之间转移。设P(X)为在距离悬崖X步的位置时获救的概率。首先，当X=10时，B必然会被A救，所以P(10)=1。当X=9时，B有1/2的概率走到10，有1/2的概率走到8，所以P(9)=P(8)*(1/2)+P(10)*(1/2)。同理可得，P(8)=P(7)*(1/2)+P(9)*(1/2)，P(7)=P(6)*(1/2)+P(8)*(1/2)…，P(1)=P(0)*(1/2)+P(2)*(1/2)。当B站在悬崖边缘，也就是X=0时，他有1/2的概率掉下去，有1/2的概率走到距离悬崖为2的地方，所以P(0)=0*(1/2)+P(1)*(1/2)。会发现0，P(0)，P(1)，…，P(10)是一个等差数列，解得P(0)=1/11。B听上去被坑了的样子。
（3）A有个不透明袋子，袋中有a个红球，b个白球。他还有无限个白球。所有的球质量、材料、形状、大小都完全一样。A让B去摸球，无论摸出的是什么颜色，都会放回去一个白球。A与B约定在n次操作后袋内所有白球都给B。问n次操作后，B拿到的球的个数Xn的期望？
三、画图法
多用于几何概型。
顺便说一句，对于几何概型，必须明确随机数的生成方式。如果不这么做就容易出这些事故：
（1）对于半径为1的圆O，随机求一条弦AB，问AB>
的概率。
a.在圆O上随机取点A,B，连接AB得出弦AB。这样相当于先固定A点（因为第一个点在哪都一样），再随机取B点。
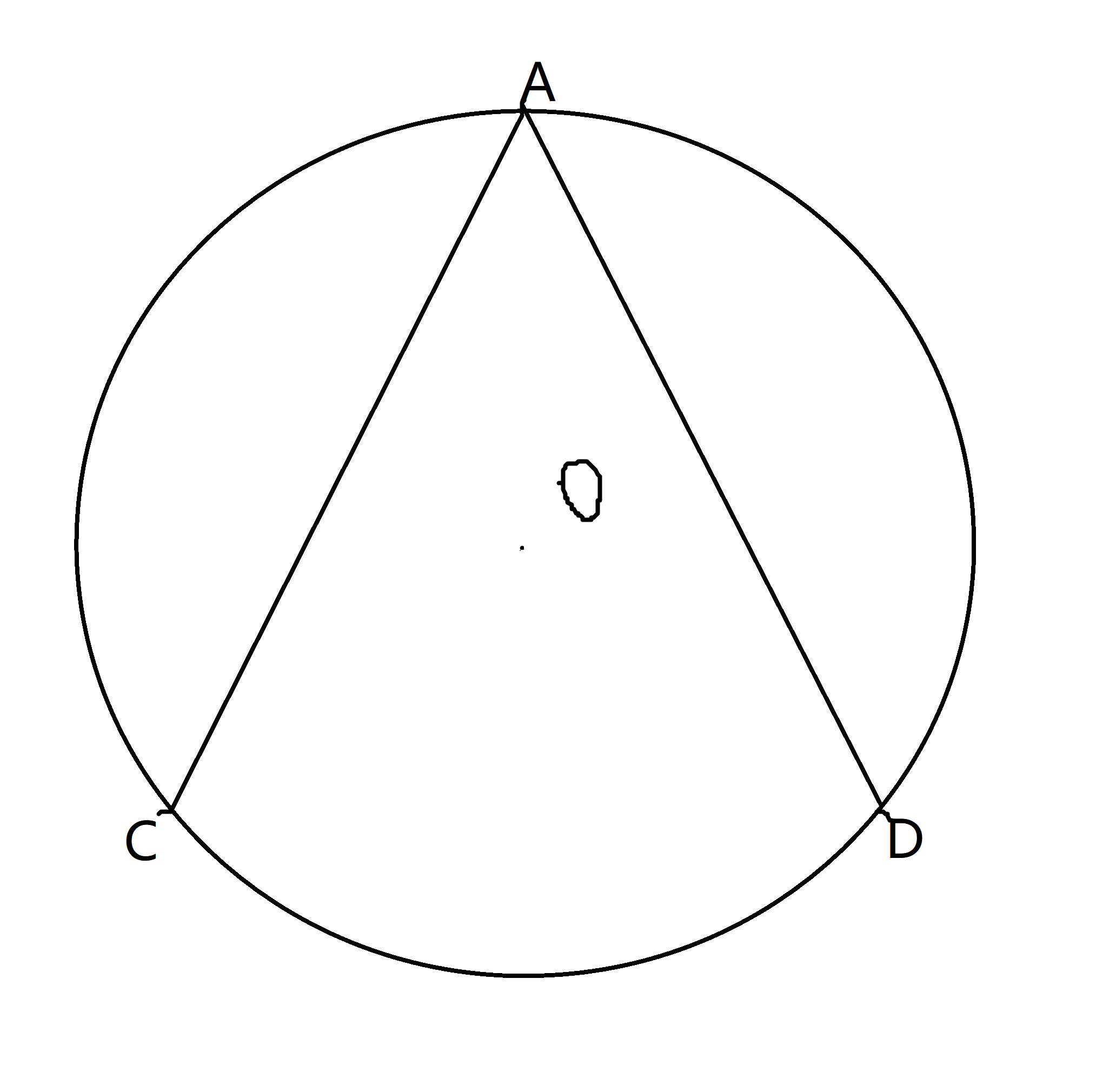
如图，弧AC等于弧CD等于弧AD。当B在弧AC上或在弧AD上时，AB<，当B在弧CD上时，AB＞。弧CD占整个圆的1/3，所以AB＞的概率是1/3。
b.取弦AB中点M，会发现当OM<1/2时AB>。
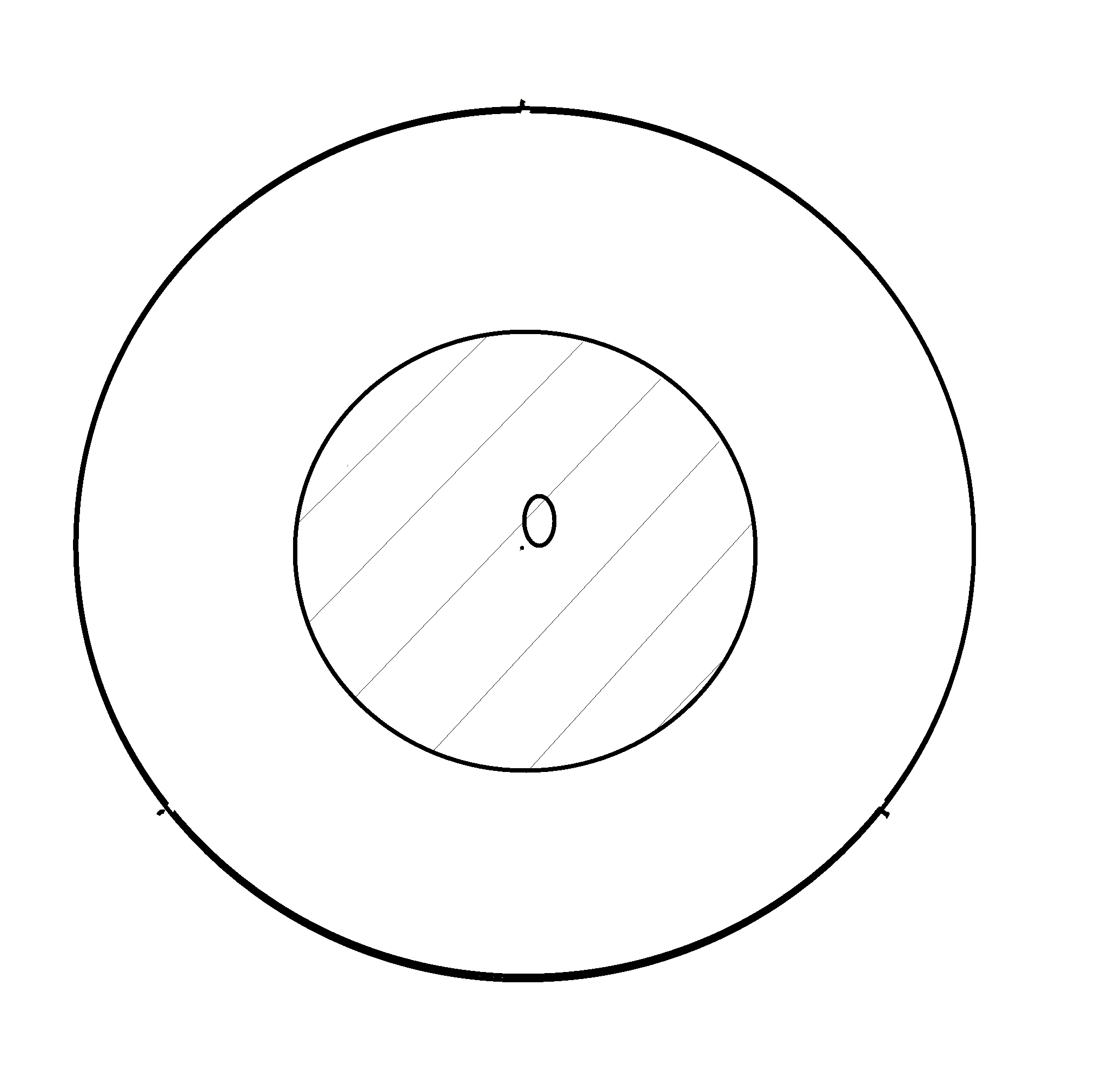
如图，以O为圆心，以1/2为半径，作小圆O。当点M在小圆O内部时，AB>。小圆O的面积是大圆O的1/4，所以AB>的概率是1/4。
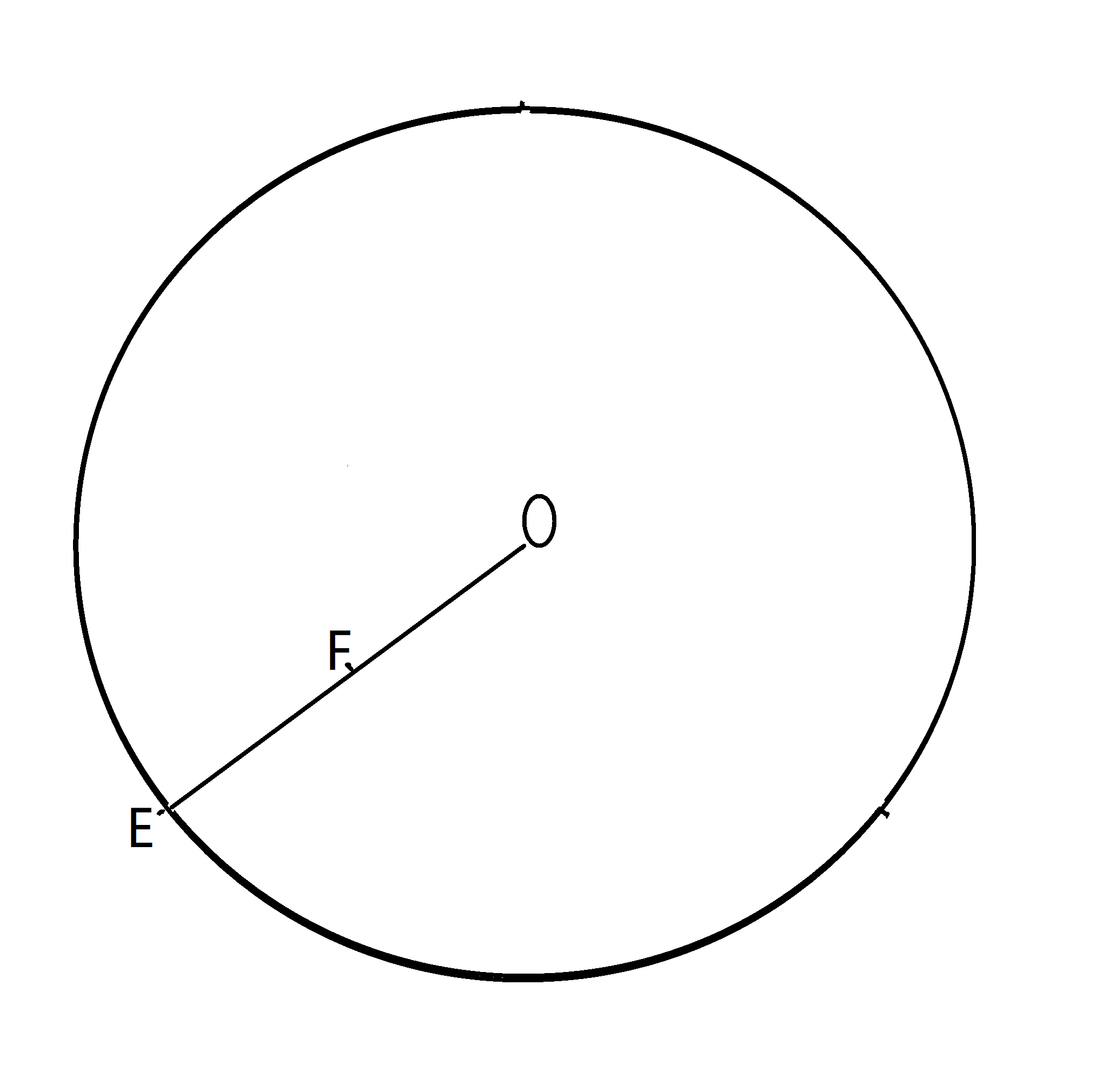
如图，作半径OE，取线段OE的中点F。当M在线段OF上时，AB>。OF=(1/2)OE，所以AB>的概率是1/2。
（2）在直角三角形ABC中，
，
，AC=1，随机取一点M,问
的概率。
在边AC、AB、BC、整个平面上、三角形里、某个角里取点的答案都是不同的。
下面是几道画图法的例题：
（1）平面上有无数条两两平行的直线，相邻两条之间距离为d。现在往平面上投一根针，针的长度为l (l<d)，问针与直线有交点的概率？
（2）圆周上随机取三点A，B，C，问圆心O在以这三个点为顶点的概率？
（3）有一根长度为1的棍子，随机取棍子上两点，在这两点处切开棍子，使它断为三段。问这三段能拼成一个三角形的概率？
（4）A早上会在7:00-8:00中随机一个时刻出发去学校，B早上会在6:30-7:30中随机一个时刻去拜访A。问B见到A的概率？
某道神题（因为不知道该如何归类）：共有2n+1个元件，每一个有p的概率正常工作，当正常工作的总数达到n+1个时，整个系统才能正常工作。问：当p=1/2时，系统正常工作的概率是多少？写出系统正常工作的概率f(n)的递推式？
To be continued......
宣传一波广义呕吐之光（现在是电教了（现在是电教G了（现在是电教X了（现在是电教XX了））））：
