网络流

一、网络流

一个有向图满足一定的条件后就可称为网络流图。

如下面的有向图就是一个网络流图：

由图可知，网络流相较于有向图的特征为：

• 有唯一的源点S
• 有唯一的汇点T
• 每条弧都有一非负容量c[u][v]

也就是说，只要一个有向图有上面3个特征，这个图就是网络流。

二、网络流的性质

1. 每条弧上有两个量，即容量c[u][v]和流量f[u][v]，且满足f[u][v]<=c[u][v]；
   
2. 若容量c[u][v]==0，则说明弧<u,v>不存在；
3. 除点S和点T外，其余点的流入量==流出量 。

【联系实际解释网络流】

通常可以把这些边想象成道路，流量就是这条道路的车流量，容量就是道路可承受的最大的车流量。很显然的，流量<=容量。而对于每个不是源点和汇点的点来说，可以类比的想象成没有存储功能的货物的中转站，所有“进入”他们的流量和等于所有从他本身“出去”的流量。

三、可行流

• 每条弧上都给定一个实数f[u][v]作为这条弧上的流量，且0 =< f[u][v] <= c[u][v]

可行流：指这样的一个流，它能从源点流到汇点。（间接的意思是，在弧的容量并不一定完整的情况下，这个流的流量不会超过它流到汇点所经过的任何一条弧的当时容量）

四、最大流

最大流：一个数值，表示从源点S到汇点T的最大流量。

举例示意：把源点比作工厂的话，最大流就是在不能超过道路的容量限制的前提下，能从工厂发出的最多货物。

最大流问题：求在满足网络流性质的情况下，从源点 s 到汇点 t 的最大流量。

举例示意：在不能超过道路的容量限制的前提下，求从工厂最多可以发出多少货物。

例：下面这个网络流的最大流为3 （每条弧上便是“流量/容量”）

五、残量网络&增广路&反向弧

【残量网络】

• 为了更方便算法的实现，一般根据原网络定义一个残量网络。
• 其中r[u][v]为残量网络的容量，有 r[u][v] = c[u][v] – f[u][v]，通俗地讲：就是对于某一条弧，还能再有多少流量经过。
• Gf表示残量网络，Ef表示残量网络的边集

例如，下图是一个网络流：

那么这个网络流的残量网络就如下图所示：

注释：由于r[s][v1] = 0，所以在残量网络中并没有弧<s,v1>

举例说明：r[v1][s] = c[v1][s] - f[v1][s] = 0 - (-f[s][v1]) = f[s][v1] = 4

【反向弧】

• 在上面的残量网络图中，像<v1,s>这样的弧称为反向弧。
• r[v1][s]表示从v1到s还可以增加4单位的流量。

但是从v1到s不是和原网络中的弧的方向相反吗？显然“从v1到s还可以增加4单位流量”这条信息毫无意义。那么，有必要建立这些反向弧吗？

在下面这个网络流图中的画出来的不是一个最大流：

但是，如果我们把s --->v2 --->v1 --->t这条路径经过的弧的流量都增加2,就得到了该网络的最大流。

注意到这条路径经过了一条反向弧<v2,v1>。

如果不设立反向弧，算法就不能发现这条路径。

从本质上说，后向弧为算法纠正自己所犯的错误提供了可能性，它允许算法取消先前的错误的行为（让2单位的流从v1流到v2)
注意：后向弧只是概念上的，在程序中后向弧与前向弧并无区别。

【增广路】

定义：在残量网络中的一条从s通往t的路径，其中任意一条弧<u,v>，都有r[u][v]>0 。

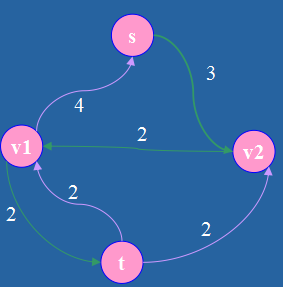
如图绿色的即为一条增广路。

【增广路算法】

• 每次用BFS找一条最短的增广路径，然后沿着这条路径修改流量值（实际修改的是残量网络的边权）。当没有增广路时，算法停止，此时的流就是最大流。

增广路算法的效率：

设n = |V|，m = |E|

每次增广都是一次BFS，效率为O(m)，而在最坏的情况下需要（n-2）次增广。（即除源点和汇点外其他点都没有连通，所有点都只和s与t连通）

所以，总共的时间复杂度为O(m*n)，所以在稀疏图中效率还是比较高的。

六、补充

【网络流的3个性质】

1、容量限制：f[u][v]<=c[u][v]
2、反对称性：f[u][v]==-f[v][u]
3、流量平衡：对于不是源点也不是汇点的任意结点，流入该结点的流量等于流出该结点的流量 只要满足这三个性质，就是一个合法的网络流。

【最大流定理】

• 如果残留网络上找不到增广路径，则当前流为最大流；反之，如果当前流不为最大流，则一定有增广路径。

【可行流】

• 假如所有边上的流量都没有超过容量(不大于容量)，那么就把这一组流量，或者说，这个流，称为一个可行流。

【增广路】

1. 我们就从零流开始考虑，假如有这么一条路，这条路从源点开始一段一段地连到了汇点，并且这条路上的每一段都满足流量<容量；（是严格的<，而不是<=）
2. 那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的；
3. 这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。

注意：

• 我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止；
• 当找不到增广路的时候，当前的流量就是最大流。

补充：

1. 寻找增广路的时候我们可以简单的从源点开始做BFS，并不断修改这条路上的delta量，直到找到源点或者找不到增广路。
2. 在程序实现的时候，我们通常只是用一个c数组来记录容量，而不记录流量，当流量+delta的时候，我们可以通过容量-delta来实现，以方便程序的实现。

【反向弧】

我们为何要加入反向弧：

在做增广路时可能会阻塞后面的增广路，或者说，做增广路本来是有个顺序才能找完最大流的。但我们是任意找的，为了修正，就每次将流量加在了反向弧上，让后面的流能够进行自我调整。

举例说明：

比如说下面这个网络流模型

我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。

于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但是，这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？

问题就在于我们没有给程序一个“后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。

那么如何解决这个问题呢？

回溯搜索吗？那么我们的效率就上升到指数级了。

这个算法神奇的利用了一个叫做反向弧的概念来解决这个问题。即每条弧<i,j>都有一条反向弧<j,i>，反向弧也同样有它的容量，容量为c[j][i] = -f[i][j] 。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。

• c[x][y] -= delta
• c[y][x] +=delta

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下：

这时再找增广路的时候，就会找到1-3-2-4这条可增广路，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

那么，这么做为什么会是对的呢？

事实上，当我们第二次的增广路走3-2这条反向弧的时候，就相当于把2-3这条正向弧已经是用了的流量给“退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。

如果这里没有2-4怎么办？

这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点

同时本来在3-4上的流量由1-3-4这条路来“接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流。

【加强理解】

有一网络流如图-4所示：

图-4的残量网络如图-5所示：

如何变成残量网络：对于已经找到一条从S到T的路径的网络中，只要在这条路径上，把c[u][v]的值更新为c[u][v]-f[u][v]，并且添加反向弧c[v][u]

提示：此外在未做任何操作之前，原始的有向图也是一个残量网络，它仅仅是未做任何更新而已。

残量网络：给定图G和流量f，残量网络Gf就是由那些仍有空间对流量进行增加的弧构成。在流网络中, 若某条弧的流量小于其容量，则将其加入的Gf中；若某条弧流量等于其容量，则这条弧将不属于Gf（看图-5，有两条这样的边已被标记成灰的，即不属于残量网络）。

增广路：残量网络Gf中一条从源节点S到汇点T的简单路径。

图-5中的增广路有：S-A-C-B-D-E-T

图-4中的增广路有：1-2-4-7 和 1-3-4-7　　（注意：原始的有向图也是一个残量网络）

【割】

网络流G(V,E)的割(S,T)将V划分成为S和T=V-S两部分，使得s∈S，t∈T。

如果f是一个流，则穿过割(S,T)的净流被定义为f(S,T)=∑f(x,y) (x∈S,y∈T)，割(S,T)的容量为c(S,T)。

一个网络的最小割就是网络中所有割中具有最小容量的割。

设f为G中的一个流，且(S,T)是G中的一个割，则通过割(S,T)的净流f(S,T)=|f|。

因为f(S,T)=f(S,V)-f(S,S)=f(S,V)=f(s,V)+f(S-s,V)=f(s,V)=|f|（这里的公式根据f(X,Y)=∑f(x,y) (x∈X,y∈Y)的定义，以及前面的三个限制应该还是可以推出来的，这里就不细讲了）。

有了上面这个定理，我们可以知道当把流不断增大时，流f的值|f|不断的接近最小割的容量直到相等，如果这时可以再增大流f，则f必定会超过某个最小的割得容量，则就会存在一个f(S,T)<=c(S,T)<|f|，显然根据上面的定理这是不可能。所以最大流必定不超过网络最小割的容量。

【最大流最小割定理】

如果f是具有源s和汇点t的流网络G=(V,E)中的一个流，则下列条件是等价的：

1. f是G中一个最大流。
2. 残留网络Gf不包含增广路径。
3. 对G的某个割(S,T)，有|f|=c(S,T)。　　（|f|是流量值）

【顶点的层次】

残留网络：设有容量网络G(V,E)及其上的网络流f，G关于f的残留网络即为G(V',E')，其中G’的顶点集V'和G的顶点集V相同，即V'=V，对于G中任何一条弧<u,v>,如果f(u,v)<c(u,v)，那么在G'中有一条弧<u,v>∈E'，其容量为c'(u,v)=c(u,v)-f(u,v)，如果f(u,v)>0,则在G'中有一条弧<v,u>∈E'，其容量为c’(v,u)=f(u,v).

从残留网络的定义来看，原容量网络中的每条弧在残留网络中都化为一条或者两条弧。在残留网络中，从源点到汇点的任意一条简单路径都对应一条增光路，路径上每条弧容量的最小值即为能够一次增广的最大流量。

顶点的层次：在残留网络中，把从源点到顶点u的最短路径长度，称为顶点u的层次。源点 Vs的层次为0.例如下图就是一个分层的过程。

注意：

（1）对残留网路进行分层后，弧可能有3种可能的情况。

1、从第i层顶点指向第i+1层顶点。

2、从第i层顶点指向第i层顶点。

3、从第i层顶点指向第j层顶点（j < i）。

（2）不存在从第i层顶点指向第i+k层顶点的弧(k>=2)。

（3）并非所有的网络都能分层。