概念
首先,我们要了解LCA的概念。
什么是LCA??????
让我们看一副图
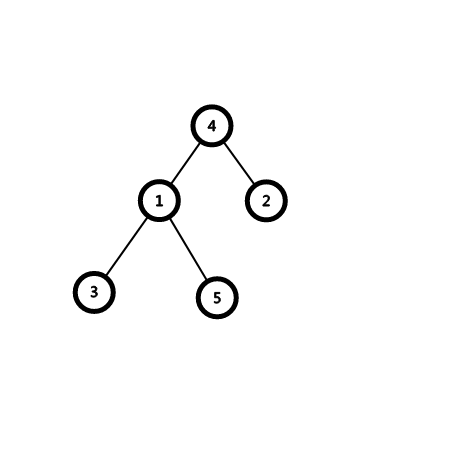
然后,我们要查找(2),(4)的最近公共祖先。
显然我们找到的是(4)。
那么,我们就可以知道,最近公共祖先就是(color{#FF0000}{两个节点在这棵树上深度最大的公共的祖先节点})
换句话说,也就是(color{#FF0000}{两个点在这棵树上距离最近的公共祖先节点})
做法
一般来说,我们会想到(color{#FF0000}{暴力}):对于每个询问,遍历所有的点,时间复杂度为O(n*q),很明显,(color{#FF0000}{n和q一般不会很小})。
(But) 在洛谷中,我们可以得70分。
在这里,我来分享一下。
暴力
// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
const int maxn=500000+5;
vector <int> e[maxn];//vector,相信没有人不会
int d[maxn],f[maxn];
/*
d[i]指i节点的深度
f[i]指i节点的父亲节点
*/
void dfs(int x,int fa){
d[x]=d[fa]+1;//求深度
f[x]=fa;
for(int i=0;i<e[x].size();i++){
int y=e[x][i];
if(y!=fa)dfs(y,x);//由于存边时存的时无向边,所以要防止搜回父亲节点,但也可以用一个vis[]来标记查过的节点
}
}
int main(){
int n,m,s;
cin>>n>>m>>s;
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
e[x].push_back(y);
e[y].push_back(x);//存边
}
dfs(s,0);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
if(d[x]<d[y]){int tmp=x;x=y;y=tmp;}//将顺序调成x<y,可以用swap()
while(d[x]>d[y]){x=f[x];}
while(x!=y){
x=f[x];y=f[y];
}//如果x!=y,就搜它们的父亲节点(很慢很慢)
printf("%d
",x);
}
return 0;
}
接下来,我们来拿满分(AC)
倍增(这一部分转自(jarjingx)的(csdn))
序言
我认为吧,所有能够优化复杂度的算法都是神奇的,所有能够化繁琐为形象的文字都是伟大的。一直觉得倍增算法是个很神奇的东西,所以决定写点东西纪念一下它。但是作为一个非常不称职的OIER,我非常讨厌在看别人的算法解析时整版的i,j,k等我看到鼠标就惯性移到右上角的符号语言,所以我想用最形象的方式来纪念它。
一
从前,有一只可爱得不得了的小白兔,它想从A地去往遥远的B地。

2B小白兔:
向右边跳一步,左边跳一步,再向右边跳很多步,再……(对不起,这个太脑残了)
普通小白兔:
向右边跳一步,再跳一步,再跳一步……再跳一步,哇,到了!好开心!
超级小白兔:
向右边跳一大步,一步跳到B,然后默默回头,鄙视一下那只一步一步跳的小白兔。
我相信作为一个正常人,是不会考虑到2B小白兔的这种做法的,因为它太脑残了。
同时我也相信,作为一个正常人,也不会考虑到超级小白兔的这种做法的,因为……
“我擦!你什么时候说可以这样跳了!(愤怒)”
“我什么时候说不可以了!(卖萌)”
但是你不得不承认,超级小白兔还是有两把刷子的,因为它真的是太厉害了,厉害得你想都没有想到。
二
从前,有一只可爱得不得了的小白兔,它想从A地去往遥远的B、C、D、E、F这几个让它魂牵梦萦的地方。(不要问我从哪里来,我的梦想在远方)

2B小白兔:
(对不起,我的生命有限,我不想再提到它了)
普通小白兔:
一步又一步,生命不息,跳跃不止。
超级小白兔:
一步到B,再一步到C,再一步到D,再一步到E,再一步到F,完工。
你不用解释,我深知你就想当那只超级小白兔,哼,你肯定是那样跳的。(神马?不是?兄弟你的智商我救不了了……)
是的,不这样跳的人对不起社会啊,浪费时间就是浪费青春,浪费青春就是犯罪。
好的,既然你是这样跳的,那你能告诉我你是怎么知道从A只要跳2个格子就会刚好到B的?难道你在空中使用了GPRS全球卫星定位系统?你少来好么!主页君现在都没用过这种东西,你一只白白嫩嫩下酒菜的小兔子还用这个?笑死我吗?哈哈,你一定是出发前就偷偷学普通兔子一步一步跳过一遍,然后拿个本子做小抄,记录好从每个格子跳任意步会到达的地方,然后赶在天亮之前回来,风光的按照踩点计划大步的跳,让我们觉得你很厉害的样子,我没说错吧?不过看在你有这个诚心的份上,还是为你的聪明鼓掌吧。
三
从前,有一只可爱得不得了的小白兔,它想从A地去往遥远的1(此处省略很多0)个地方,因为它真的是太没事情做了。

普通小白兔:
从离开家门的那天起,我就没有想过要放弃一步一步地跳往终点。(嗯,加油)
超级小白兔:
轻轻松松,绝不多走一步。(哼哼)
你想知道最后的结果吗?呵呵,好像还没有出结果……
写给普通小白兔的话:
亲爱的小白兔,我知道你勇毅,你质朴,但是,苦海无涯,回头是岸。
写给超级小白兔的话:
我不知道你的小抄本是否还够用,我不知道你摸着黑就出门是为了什么,你不觉得你的行踪早就已经暴露了吗?你以为你很聪明吗?不,你错了,你就一下酒菜,永远都是,因为你不知道倍增算法,这是你失败的根源,再见,我心中永远不会逝去的蠢兔子。
——————————————————分割线————————————————————
普通兔子 = 速度慢,无资源损耗 || 超级兔子 = 速度快,多资源损耗
还记得那只离我们远去的2B兔子吗?对,其实我们早该想到了,越蠢得不可思议的兔子身上竟然有巨大的宝藏,再看看它的名字吧,“2B”!去掉一个“B”!就是“2”!对,你没有听错,就是“2”,你能想到4、8、16、32吗?
再想想,超级兔子的小抄本不够用,不就是因为它为了应对所有的目的地信息,它记录下了任何一个格子跳任意步会到达的格子,100个格子它要记录大概5000条信息,1000个格子大概要记录500000条信息,10000个格子它大概要记录50000000条信息,至于你晕没晕,我相信它应该晕了。
可不可以把记录的信息数降到最低呢?当然可以,2B兔子帮你忙,让你用2战胜敌人。
当你只记录任何一个格子跳1、2、4、8、16……步会到达的格子的时候,你有没有发现信息数突然少了好多好多啊!真的少了好多好多啊!100个格子只要500条左右,1000个格子只要5000条左右,10000个格子只要50000条左右,不比不知道,一比吓一跳啊!
安心小抄五十年,健康生活一辈子。
——————————————————分割线————————————————————
从此,超级小白兔成为了聪明小白兔,它的生活是这样的:

在夜深人静的时候,它偷偷出门做小抄,记录下从每个格子跳1、2、4、8……个格子后会到达的格子,然后在太阳出来后,它在众目睽睽之下,开始了表演。
从A出发:若跳8个格子(超过B了,放弃)
若跳4个格子(超过B了,放弃)
若跳2个格子(没超过B,跳吧)
若跳1个格子(没超过B,跳吧)
从B出发:…………
多么轻松的事情,只要一本很薄的小抄就可以了,最关键的是:它绝对不会连着跳两步都是跳相同的格子数,因为如果跳两次2个格子都是可行的话,那么它干嘛不跳4个格子捏?
我们可是从多到少来判断的啊!!
——————————————————分割线————————————————————
好的,聪明小白兔白天的事情你已经看懂了,且看它晚上是怎么打小抄的吧。

从A出发跳1步到1(记录下来)
从1出发跳1步到2(记录下来)
…………(跳1步的记录完毕)
从A出发跳2步?就是从A出发跳1步再跳1步的到的地方,翻看小抄,直接誊写从1出发跳1步会到的2这个格子作为A跳2步会到的格子。
从1出发跳2步?跟刚才一样,直接誊写。
…………(跳2步的记录完毕)
从A出发跳4步?你还真去跳4步?不,它也就是等于从A出发跳2步到的2号点再跳2步会到的格子,那么我们直接誊写2号格子跳2步会到的格子就可以了。
看看聪明小白兔多么聪明!也许还有自认为更聪明的:
“在记录A跳4步会到的格子的时候,为什么不直接从A跳4步看到了哪里再记录下来呢?跳4步跟跳1步的代价不是一样的么”
“我这样回答你好了!把你丢在纽约的一个公交车站,问你一条线路的下一个站是什么?你怎么办?当然是自己亲自走到下一个站就知道了!那如果问你接下来的第4个站是什么?难道你可以直接走到第4个站而不用途径其它的站点了吗?这不现实,你还是要一个一个站的走,因为关键在于你只能知道你目前所在站点的下一个站是什么,想知道下下个站,除非你已经到了下个站,兔子跳格子也跟这类似,虽然聪明小白兔神通广大,但是不至于伟大到可以提前预知跳几步会到哪里啊!!”
从此,聪明小白兔避免了成为人类的下酒菜,而被一群OIER们像神一样的供奉了起来,不要问它为什么,因为它也不知道,貌似只是某人卖了个小萌,事情就变成这样了。
倍增代码
//说了这么多,我们来看看代码
#include<cstdio>
#include<vector>
#include<algorithm>
#include<iostream>
using namespace std;
const int maxn=500000+5;
int father[maxn][25],n,m,s,dep[maxn];
vector<int>edge[maxn];
inline void dfs(int now,int fa){
dep[now]=dep[fa]+1;
father[now][0]=fa;
for(size_t i=0;i<edge[now].size();++i)
if(edge[now][i]!=fa)dfs(edge[now][i],now);
}
inline void init(){
for(int j=1;j<=20;j++)
for(int i=1;i<=n;i++)father[i][j]=father[father[i][j-1]][j-1];//预处理(很重要!很重要!)
}
inline int lca(int a,int b){
if(dep[a]<dep[b])swap(a,b);
for(int i=20;i>=0;--i){
if(dep[father[a][i]]>=dep[b])a=father[a][i];//倍增
}
if(a==b)return a;
for(int i=20;i>=0;--i)
if(father[a][i]!=father[b][i]){
a=father[a][i];
b=father[b][i];
}//还是
return father[a][0];
}
int read() {
int x=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch<='9'&&ch>='0'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int main() {
n=read();m=read();s=read();
for(int i=1;i<n;++i){
int u,v;
u=read();v=read();
edge[u].push_back(v);
edge[v].push_back(u);//存边
}
dfs(s,0);
init();
while(m--){
int a,b;
scanf("%d%d",&a,&b);
printf("%d
",lca(a,b));//输出
}
return 0;
}