生成学习算法
判别算法：进行P(y|x)的计算或者是进行h(x)（其中h只会是0与1）的计算。
生成学习算法：进行P(x|y)的建模，即给定类的条件下，某种特征显示的结果。同时也会对P(y)进行建模。
根据贝叶斯公式，我们可以得到
，其中p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0)。实际上，如果我们计算P(y|x)进行预测，我们不必计算分母的值，因为x是独立于y的，所以
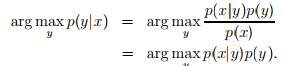argmax是当式子取到最大值时，对应参数的取值。
高斯判别分析
多元高斯分布
如果x服从多元高斯分布，那么
参数为u（均值），sigma（协方差）
u的定义为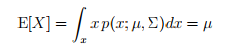
，sigma的定义为Cov(Z) = E[(Z − E[Z])(Z − E[Z])T ]。
假设x是n维向量，并且是连续值。y取0或者1，同时p(x|y)是高斯分布。 那么
对其进行最大似然估计
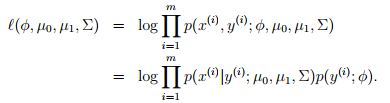，则参数的估计值为
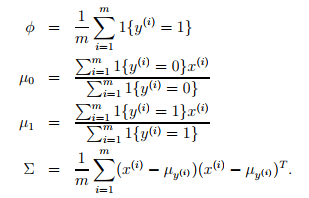
高斯判别分析与logistics回归对比
两者建模的对象不同，但是都属于分类算法，logistics回归计算的是先验概率，高斯判别分析计算的是后验概率。
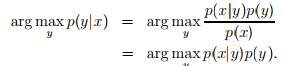如果y取任何值的概率是相等的，即p(y)不变，那么，argmaxp(y|x)=argmaxp(x|y)。
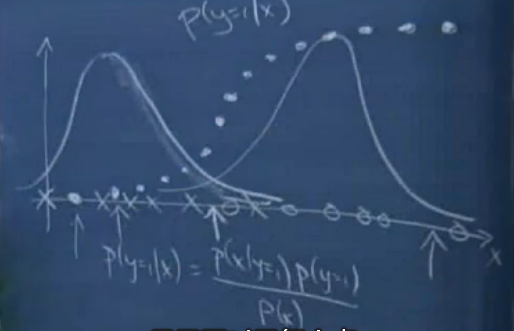
如果先对不同类别进行建模，即y取不同值得时候，进行高斯判别分析。那么就会得到两个高斯函数曲线，此处y取0，1。在高斯函数曲线基础上进行现眼概率分析，那么回得到一条类似logistics回归曲线。
同时，如果一个模型的后验概率属于高斯判别分析，那么前验概率就属于logistics回归。但是反过来不成立，也就是说，高斯判别分析比logistics回归有更强的假设。那么就意味着如果模型的假设是正确的，高斯判别分析将更好的拟合数据，它就是一个更好的模型。对于一些小样本来说，高斯判别分析也更加适合。
然而，如果不确定x|y的分布情况，也就是高斯判别分析的假设不一定成立，那么使用logistics回归更有效，因为x|y服从泊松分布等其他分布的时候，也可以推出先验概率是logistics回归曲线。事实上，只要x|y服从指数分布族，那么p（y=1|x）都可以看成logistics。
所以这是判别算法和第一个生成学习算法的比较。
朴素贝叶斯算法（Naive Bayes）
朴素贝叶斯算法是第二个生成学习算法。典型特例是垃圾邮件识别。高斯判别分析中，x向量是一个连续值。在朴素贝叶斯中，x向量是不连续的。
通过训练样本来对垃圾邮件进行标识，即
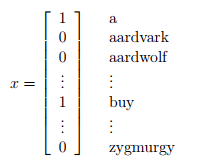如果该词出现，则标记为1，否则为0。此时要对p（x｜y）和p（y）进行建模，假设字典中有5000个字，那么x就有2^5000中可能取值，对其建模的一种方式为多项式分布法（multinomial distribution），但是此时会有2^5000-1个参数。需要用到朴素贝叶斯算法。
假设对于给定的y，xi是条件独立的（conditionally independent）,也就是说，如果一封邮件被标记为垃圾邮件，那么该邮件里面出现的单词是独立的（并不是说，两个单词是相互独立的，而是，在给定y的条件下，两者是独立的。其实事实上，垃圾邮件里面的单词并不独立，这里只是一种假设）那么根据概率的链式法则，我们可以得到，
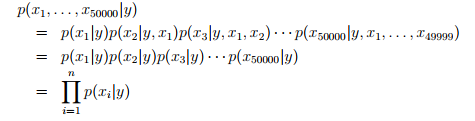那么对应的参数为
φi|y=1 = p(xi = 1|y = 1), φi|y=0 = p(xi = 1|y = 0), φy = p(y = 1)。为了得到参数，进行最大似然估计
得到参数的估计值
于是对于给定的样本特征x，可以做出以下预测
如果在你的训练样本集中从未出现过一个词，比如说nips,并且这个词是x向量中的第3500个词。由于这个词在你的训练样本中从未出现。那么垃圾邮件分类器就会进行如下估计（在正常邮件中出现的概率和垃圾邮件中出现的概率都是0）
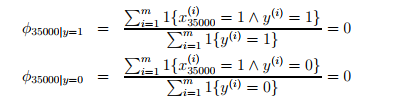
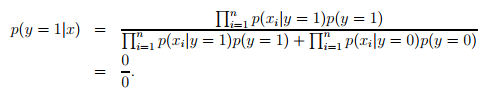此处要使用Laplace smoothing进行修正，即
