卷积神经网络(Convolutional Neural Network)
1、什么是CNN
什么卷积、为什么用CNN
2、实现CNN的步骤
input——>convolution——>max pooling——>...——>flatten——>fully connected network——>output
3、如何用keras搭建一个CNN
4、CNN分析
1、什么是CNN
1)什么卷积
1、卷积本质上是“加权求和”,在信号处理中是时间上的“加权求和”,在图像处理中是空间上的“加权求和”
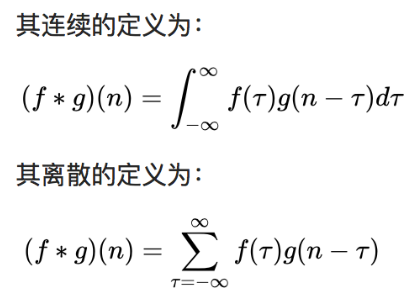
2、在信号处理中,系统的响应不仅与当前时刻系统的输入有关,也跟之前若干时刻的输入有关,比如在t3时刻的响应Y(3)=Y(0)+Y(1)+Y(2),但常常系统中不是这样的,因为0时刻的响应不太可能在1时刻仍旧未变化,那么怎么表述这种变化呢,就通过h(t)这个响应函数与x(0)相乘来表述,表述为x(m)×h(t-m),公式里的m指的 t 的变化量

参考:http://muchong.com/html/201001/1773707.html
2)为什么用CNN
- 机器识图的过程:机器识别图像并不是一下子将一个复杂的图片完整识别出来,而是将一个完整的图片分割成许多个小部分,把每个小部分里具有的特征提取出来(也就是识别每个小部分),再将这些小部分具有的特征汇总到一起,就可以完成机器识别图像的过程了。

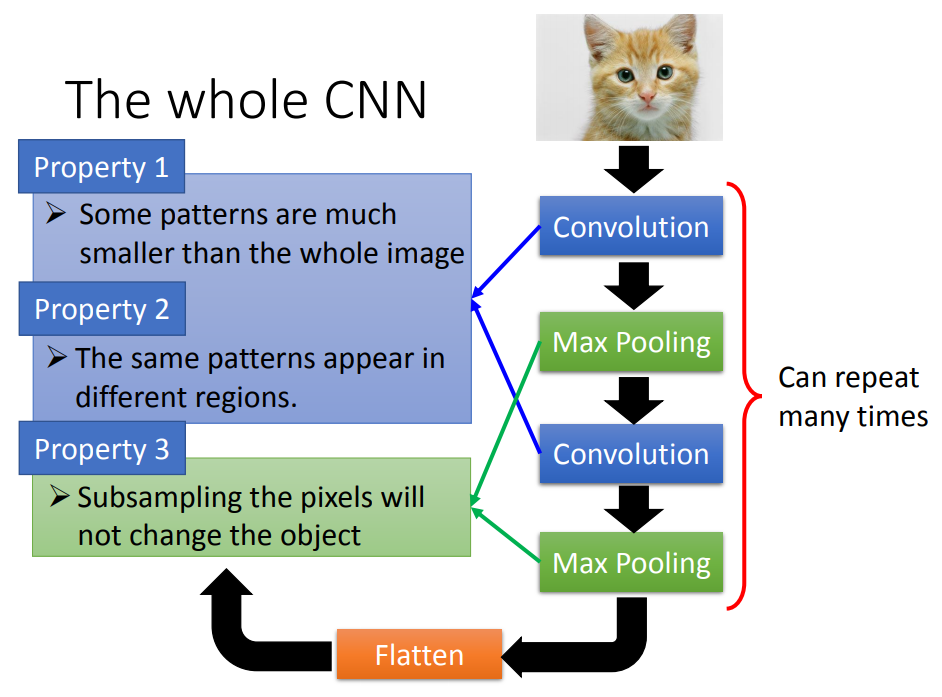
CNN的参数比全连接神经网络少得多,为什么CNN只用较少的参数就可以用于处理图像呢?这是因为图像具有以下三点特征:
- 一些特征比整张图片小得多,不用CNN的话会看完整幅图片才能确定一个特征,用CNN会认为只需要看图片的局部就可以了;
- 同样的特征可能出现在图像的不同区域,不用CNN的话会认为这两个不同位置的同一个特征是不同的特征,用CNN会认为它们是同一个;
- 对图像的降采样不会改变图像中的物体。
CNN的卷积层的设计对应着前两点,池化层的设计对应着第三点。



2、实现CNN的步骤
input——>convolution——>max pooling——>...——>flatten——>fully connected network——>output
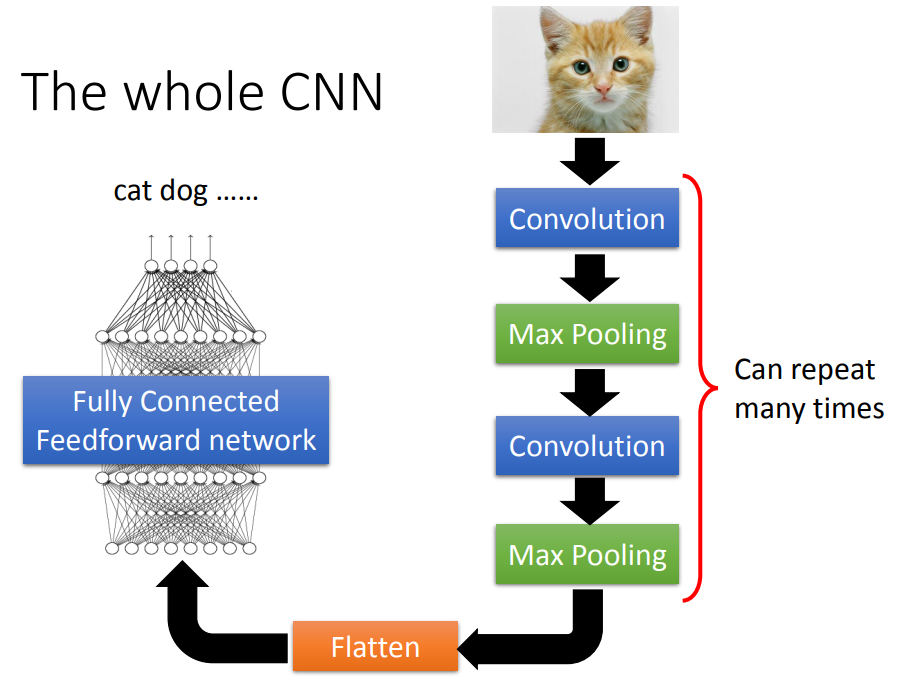
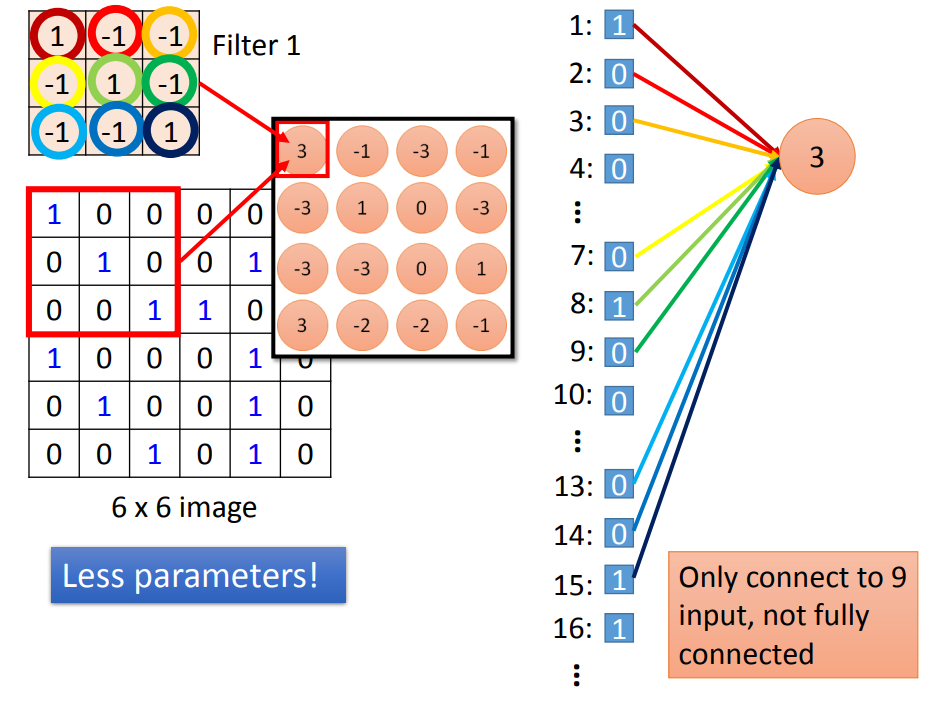
1、卷积层(减少训练参数)
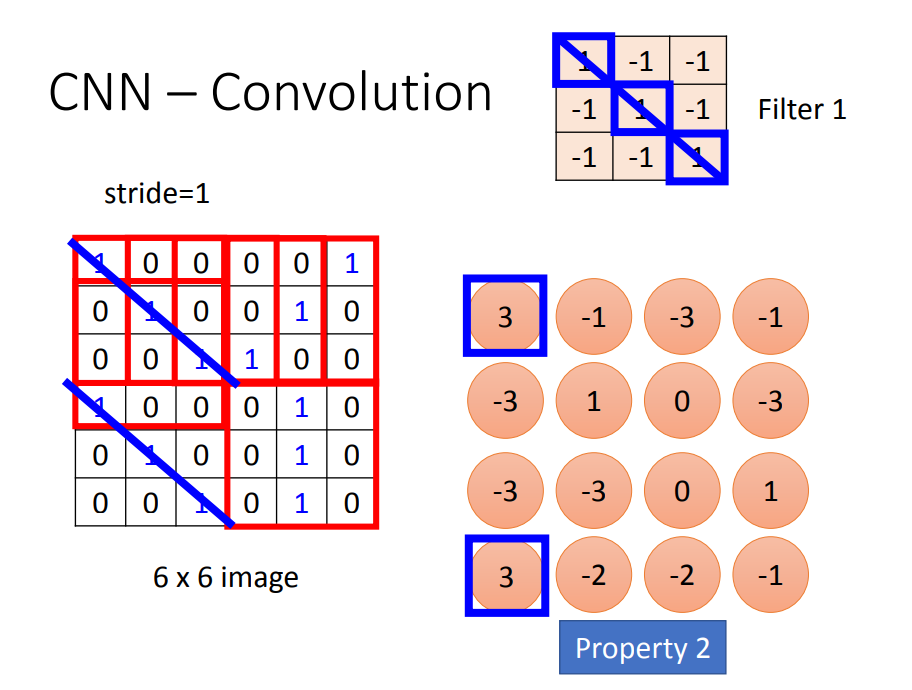
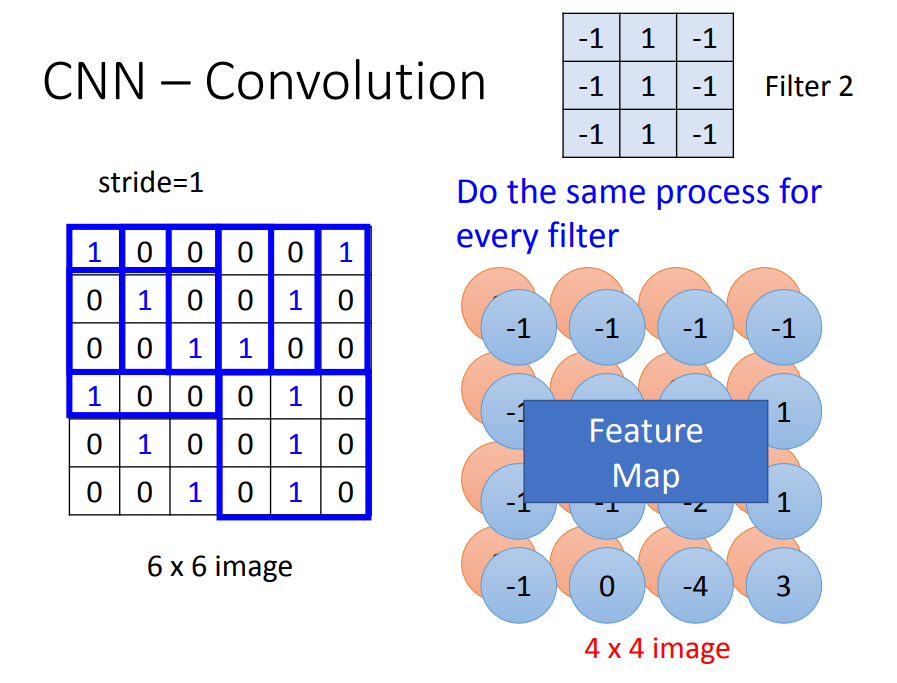
- 对应Property1:每一个Filter(待训练的参数)代表一个局部特征探测器,假设现在两个特征探测器(Filter1和Filter2)
- 对应Property2:用Filter1就能探测出在不同位置的同一个flatten,而不需要用不同的Filter
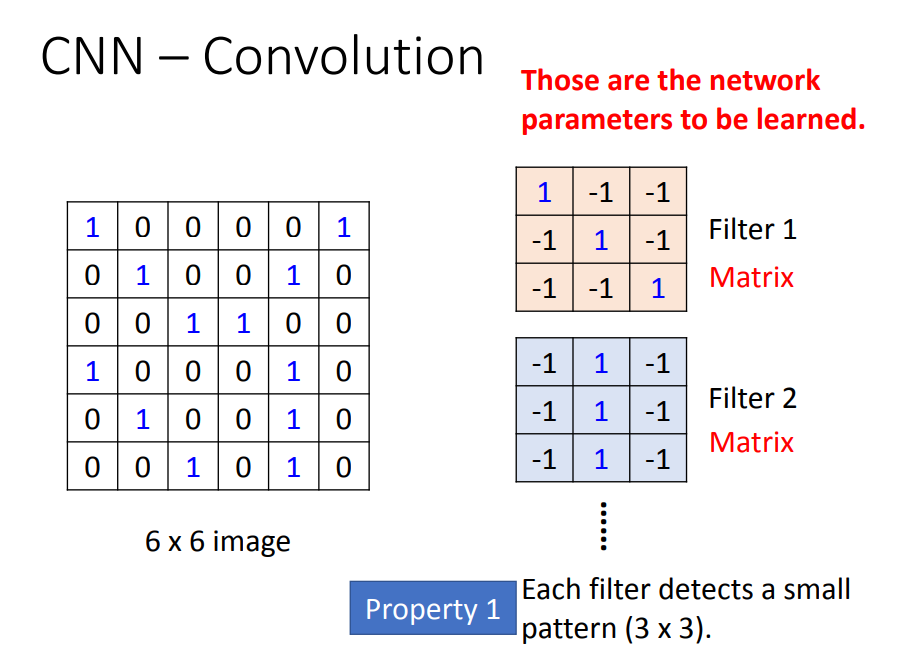
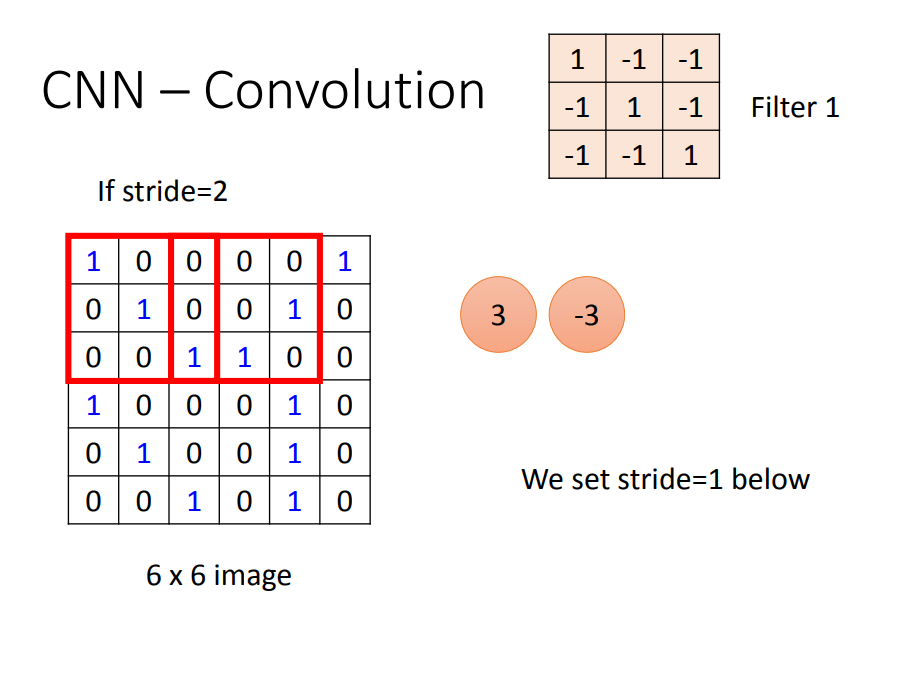
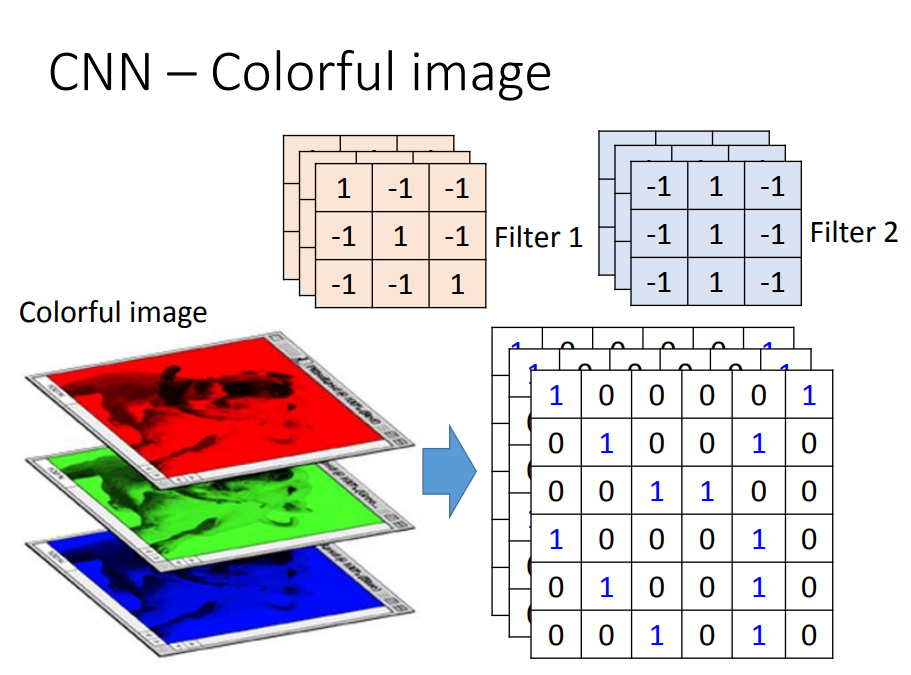
- 如果图片是彩色的,也就是说它是三通道的,还没卷积之前,可以说有3个通道,意味着每一个像素由3个数值表示。
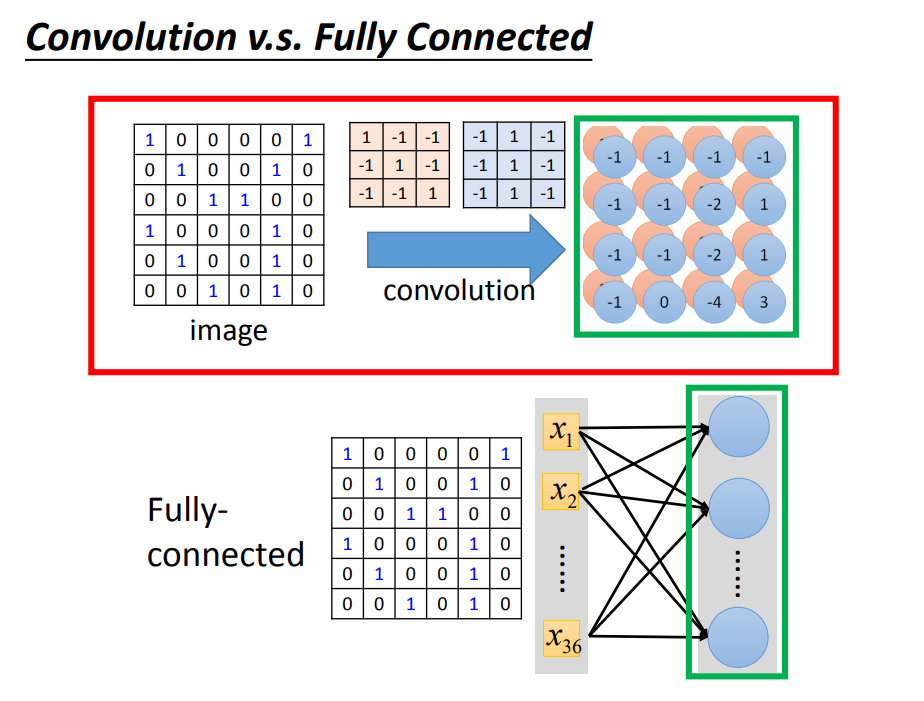
与全连接方式的对比:
- convolution的事情,就是把fully connected的部分参数拿掉
- 拿掉部分参数以后,剩下的参数权值共享

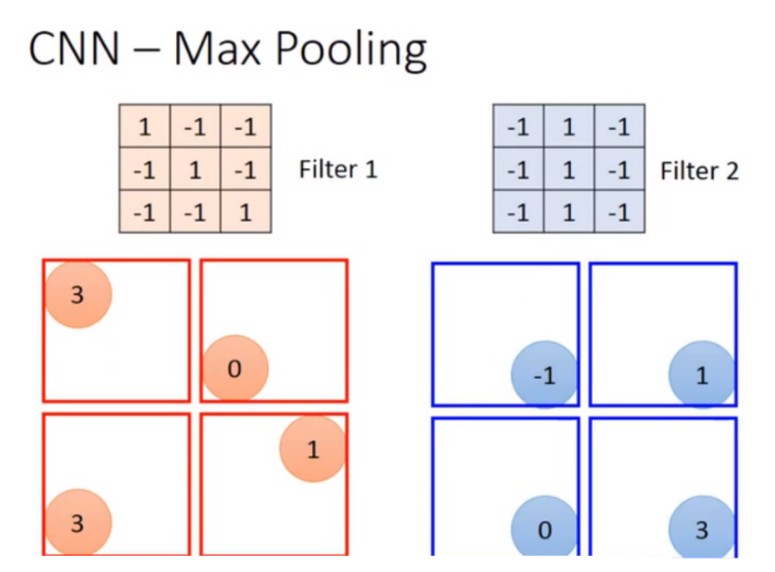
2、池化层
- 目的是减少每一个特征的维度,也就是减少后面flatten的输入特征数量


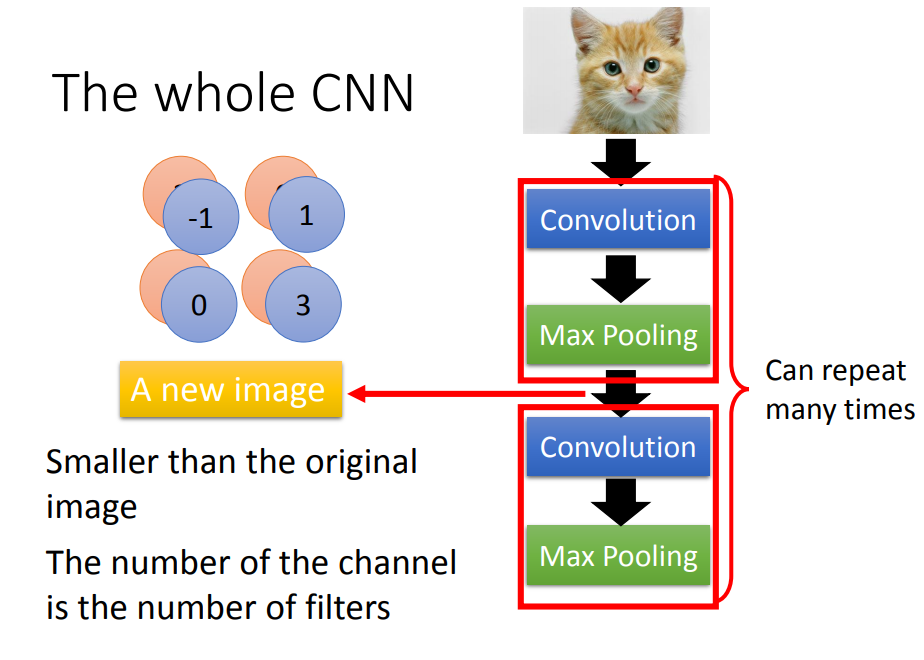
3、重复
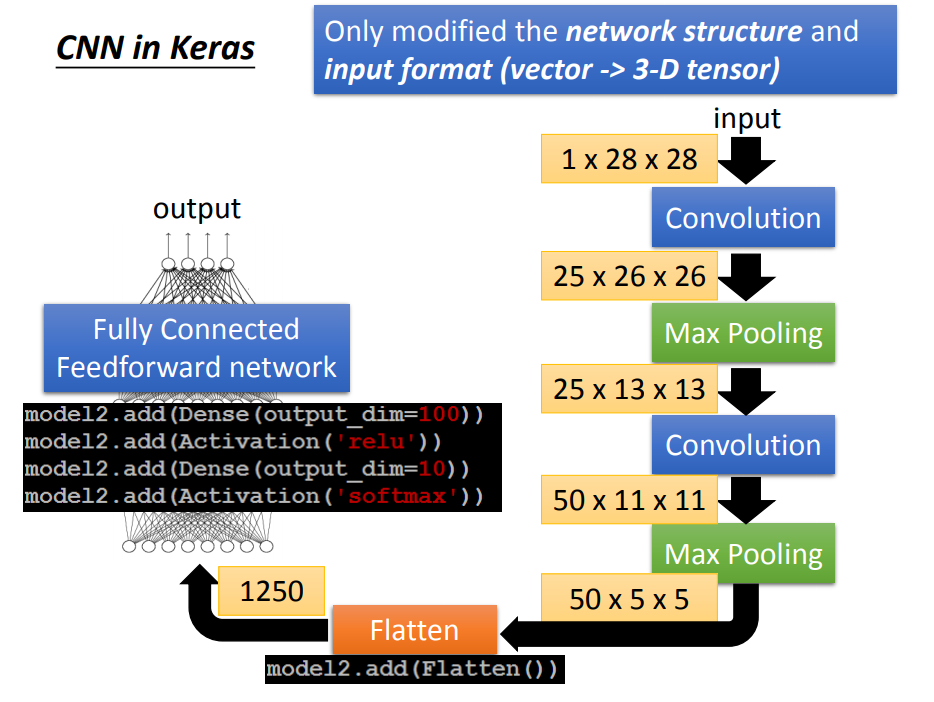
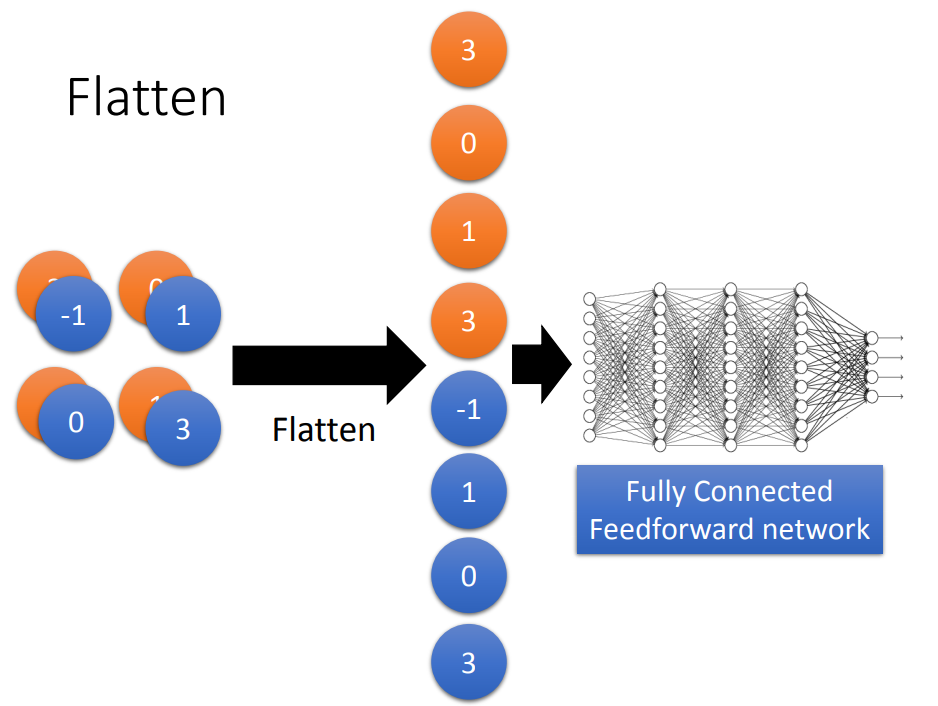
4、Flatten

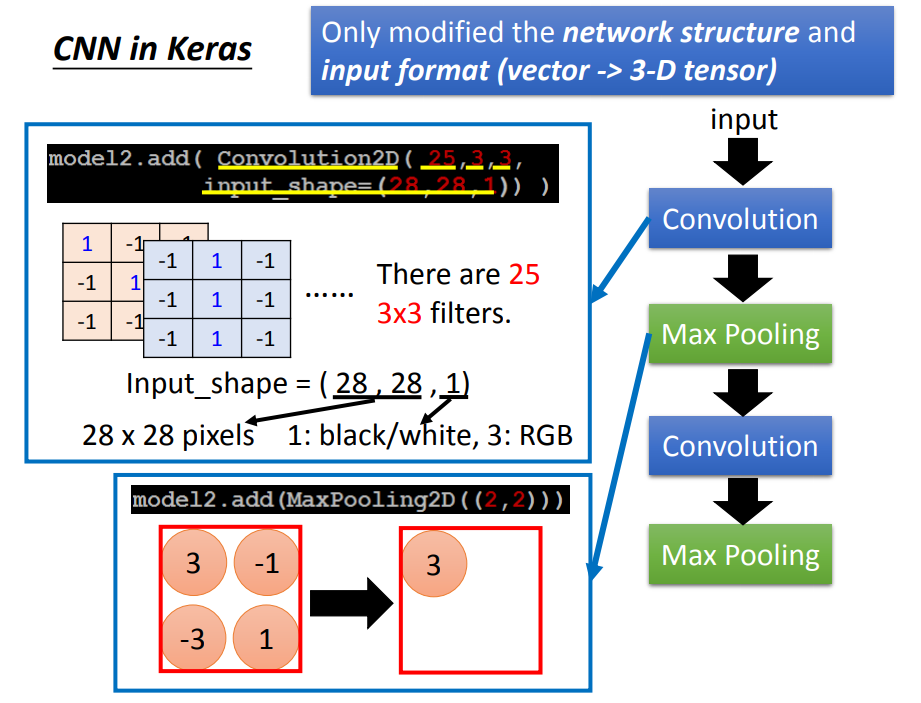
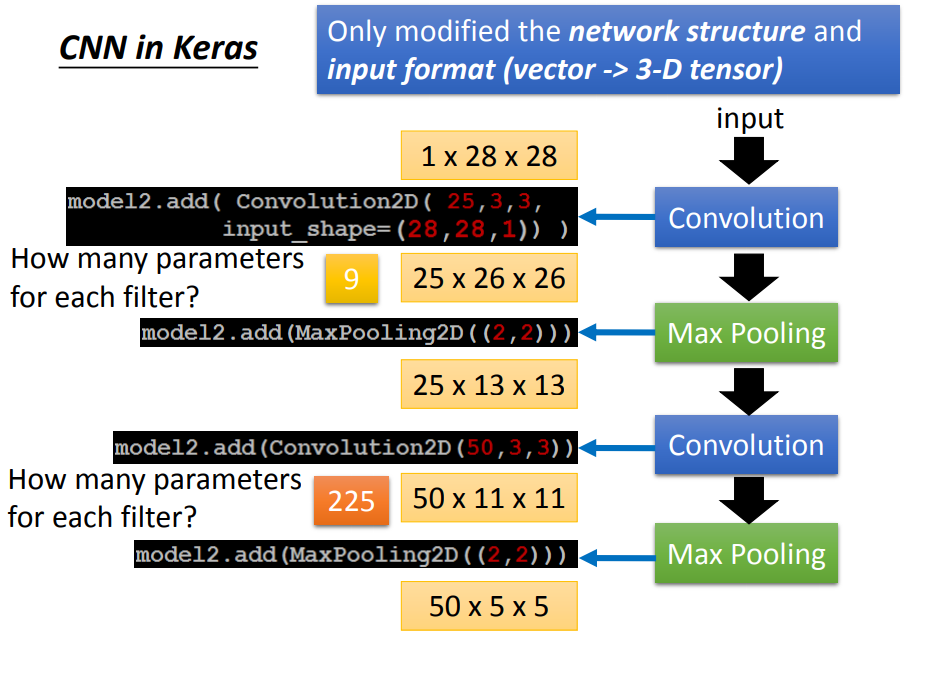
3、如何用keras搭建一个CNN
- 卷积前,一个pixel用多少个数值表示,取决于通道数
- 卷积后,一个pixel用多少个数值表示,取决于Filter个数,而通道数决定Filter的高
- 上一个卷积层有多少个Filter,下一层卷积input就有多少个通道