二叉查找树

二叉查找树（二叉搜索树或二叉排序树）是一种数据结构，采用了图的树形结构。数据存储于二叉查找树的各个节点中。每个结点最多有两个子结点，结点中的数字就是存储的数据。

1、性质

二叉查找树有两个性质。第一个是每个结点的值均大于其左子树上任意一个结点的值。比如15、8大于它左子树上任意一个结点的值。第二个是每个结点的值均小于其右子树任意一个结点的值。比如15小于其右子树上的23、17、28。

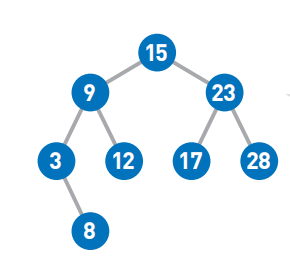
根据此，得出结论：

第一，二叉查找树的最小结点要从顶端开始，往其左下的末端寻找。比如此处最小值是3。

第二，二叉查找树的最大结点要从顶端开始，往其右下的末端寻找，这里的最大值是28。

2、添加数据

（1）添加数字1

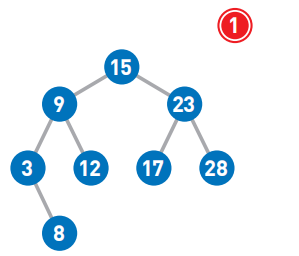
因为1<15，所以将其往左移

首先，从二叉查找树的顶端结点开始寻找添加数字的位置。将需要添加的1与该结点中的值进行比较，小于它则往左移，大于它则往右移。

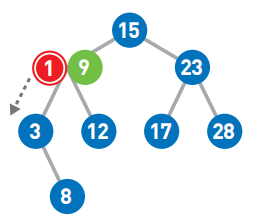
因为1<9，所以将1往左移。

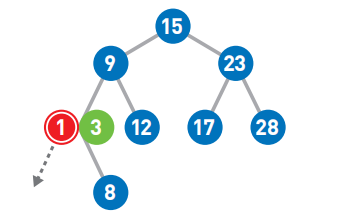
由于1<3，所以继续将1往左移，但前面没有结点了，就把1作为新结点添加到左下方。

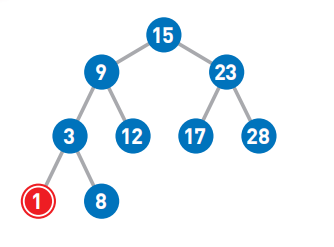
添加1的数据就完成了。

（2）添加数字4

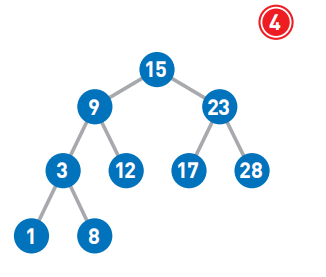
因为4<15，所以将其往右移。

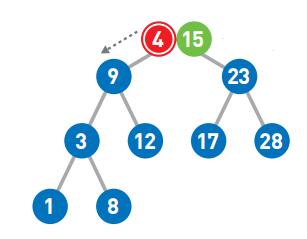
首先从二叉查找树的顶端结点开始寻找添加数字的位置。

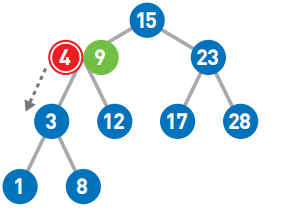
因为4<9，所以将其往左移

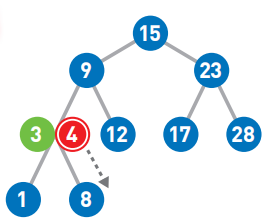
因为4>3，所以将其往右移。

因为4<8，所以需要将其往左移，但是因为前面没有结点了，所以需要把4作为新的结点添加到左下方。

于是4的添加操作就完成了。

3、删除数据

（1）删除28

如果要删除的结点没有子结点，直接进行删除该结点即可。

（2）删除结点8。

如果要删除的结点只有一个子结点，那么先删除目标结点

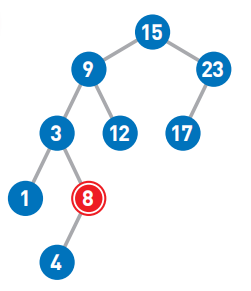
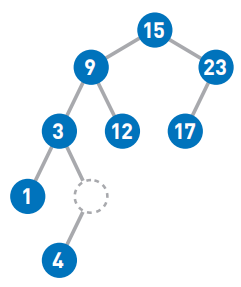
然后再把子结点移动到被删除结点的位置上。

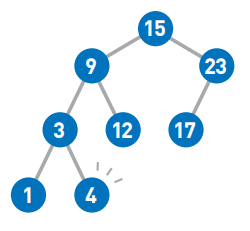
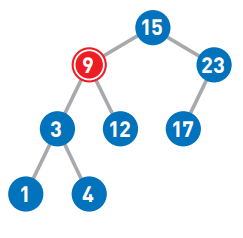
（3）删除结点9

如果删除的结点有两个子结点，那么先删除目标结点。

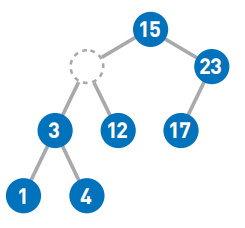
然后在被删除结点的左子树中寻找最大结点

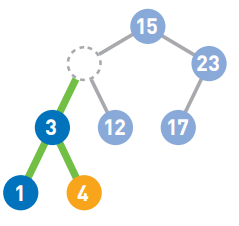
最后将最大结点移到被删除结点的位置。现在就能满足二叉查找树性质的前提下删除结点了。如果需要移动的结点还有子结点，就递归执行前面的操作。

4、查找数据

比如查找12，从二叉查找树的顶端结点开始往下查找，和添加数据一样，将12和结点中的值进行比较，小于该结点的值则左移，大于则右移。

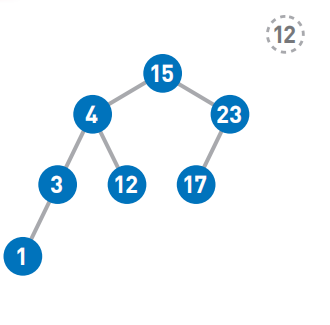
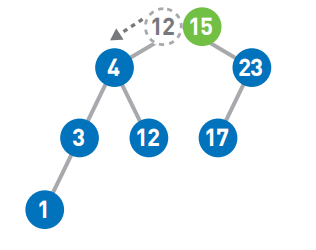
因为12>4，所以需要右移

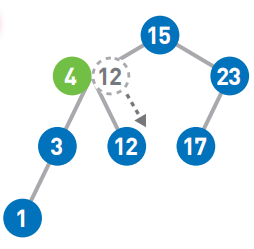
这样就找到结点12了。