快速排序是用的比较多的排序算法,比如需要对“6 1 2 7 9 3 4 5 10 8”这几个数进行排序。方法是首先在这个序列中随便找一个数作为基准数。比如找 6 作为基准数,
然后需要将这个序列中所有比基准数 6 大的数放右边,比基准数小的数放 6 的左边,类似如下排列:

初始的状态下数字 6 在序列的第 1 位,目标是将 6 挪到中间某个位置,假如这个位置为 K,就需要寻找这个 k,然后以 k 为分界点,左边的数都小于 6,右边的数都大于等于 6。方法是从初始序列“6 1 2 7 9 3 4 5 10 8”的两端进行探测,先从右边往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换他们,可以用两个变量 i 和 j,分别指向最左边和最右边,刚开始让 i 指向序列最左边即(i=1),指向数字 6。让 j 指向序列最右边(j=10),指向数字 8。

首先 j 开始出动,因为此处设置的基准数是最左边的数,所以需要 j 开始出动,一步步向左挪动,即 j--,直到找到一个小于 6 的数停下来。然后 i 开始向右挪动,即 i++,直到找到一个大于 6 的数停下来。
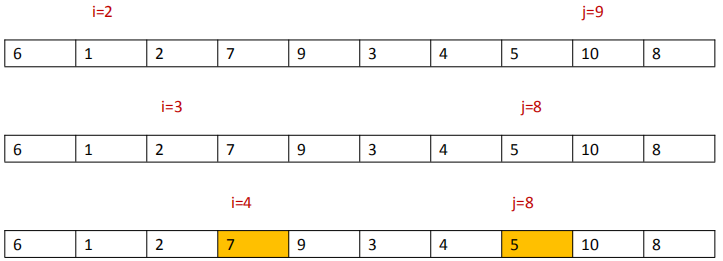
进行交换后顺序如下:

第一次交换结束,接下来 j 继续向左挪动,找到 4 比基准数小需要停下来
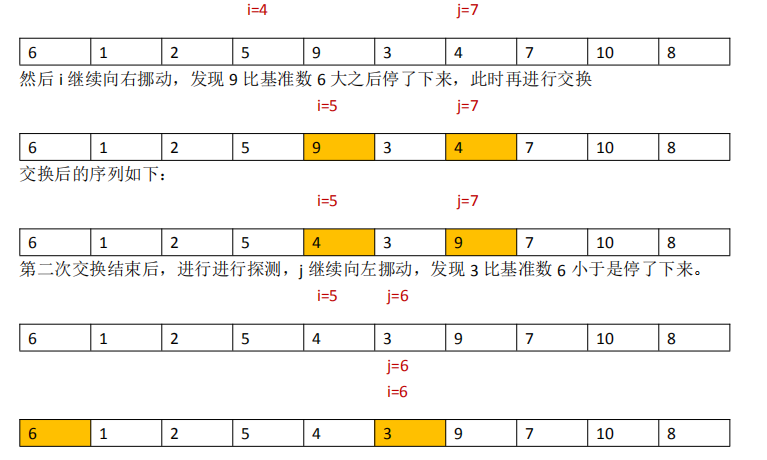

此时基准数 6 已经归位,正好处在序列的第 6 位。已经将原来的序列以 6 为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。
接下来就需要分别处理这两个序列,按照刚刚的方法分别处理 6 左边和右边的序列即可。
左边的序列是“3 1 2 5 4”,将 3 作为基准数进行调整,使得 3 左边的都是小于等于3,3 右边的都是大于等于 3。


1 package day08;
2
3
4
5 public class QuickSort {
6
7 public static void quickSort(int[] arr, int left, int right) {
8
9 int i, j, temp, t;
10
11 if (left > right) {
12
13 return;
14
15 }
16
17 i = left;
18
19 j = right;
20
21 //temp是基准位
22
23 temp = arr[left];
24
25 while (i < j) {
26
27 //j从右往左依次挪动进行递减
28
29 while (temp <= arr[j] && i < j) {
30
31 j--;
32
33 }
34
35 //i从左往右依次挪动进行递增
36
37 while (temp >= arr[i] && i < j) {
38
39 i++;
40
41 }
42
43 //如果满足条件进行交换
44
45 if (i < j) {
46
47 t = arr[j];
48
49 arr[j] = arr[i];
50
51 arr[i] = t;
52
53 }
54
55
56
57 }
58
59 //最后将基准位与i和j相等位置的数字交换
60
61 arr[left] = arr[i];
62
63 arr[i] = temp;
64
65 quickSort(arr, left, j - 1);
66
67 quickSort(arr, j + 1, right);
68
69 }
70
71
72
73 public static void main(String[] args) {
74
75 int[] arr = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8};
76
77 quickSort(arr, 0, arr.length - 1);
78
79 for (int i = 0; i < arr.length; i++) {
80
81 System.out.print(arr[i] + " ");
82
83 }
84
85 }
86
87 }
运行结果:
