今天花了半天肝下AC自动机,总算啃下一块硬骨头,熬夜把博客赶出来。。
正如许多博客所说,AC自动机看似很难很妙,而事实上不难,但的确很妙。笼统地说,AC自动机=Trie+KMP,但是仅仅知道这个并没有什么用,该写不出来的还是写不出来,必须理解每一步的精确含义。KMP算法的精髓是“用自己匹配自己”,即:如果前i个字符失配时应该转移到第j个字符,那么前i+1个字符失配时应该比较i+1与j+1处的字符。AC自动机是一样的道理,只不过将图画在一颗Trie上,看起来不像KMP那样直观。用语言去描述构造失配边时的过程是这样的:设当前结点和字符分别为u和c,父亲结点的失配边指向v,如果v下有对应c的边,那么说明u的失配边应该指向ch[v][c](因为恰好匹配,公共前缀不变);否则将u视为v的子结点(也可以理解为给v建一个虚拟子结点对应c,然后递归求解虚拟结点的失配边),去找v的失配边指向的结点,直到找到或者v为根结点。
下面用一个例子解释一下这个过程:
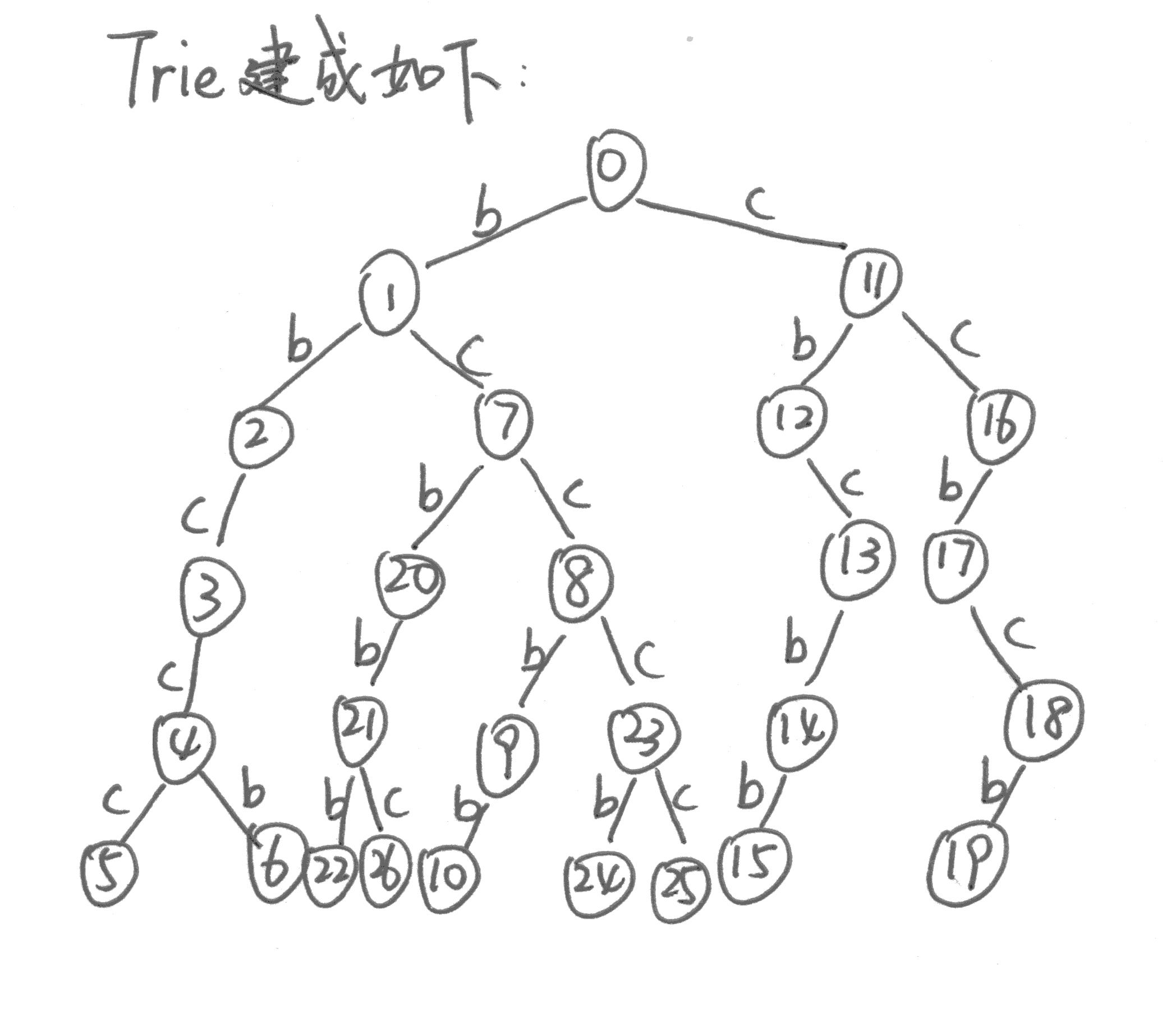
现在为Trie加入失配边(这张图有点乱,建议一个点一个点地捋,找到规律就好办了)
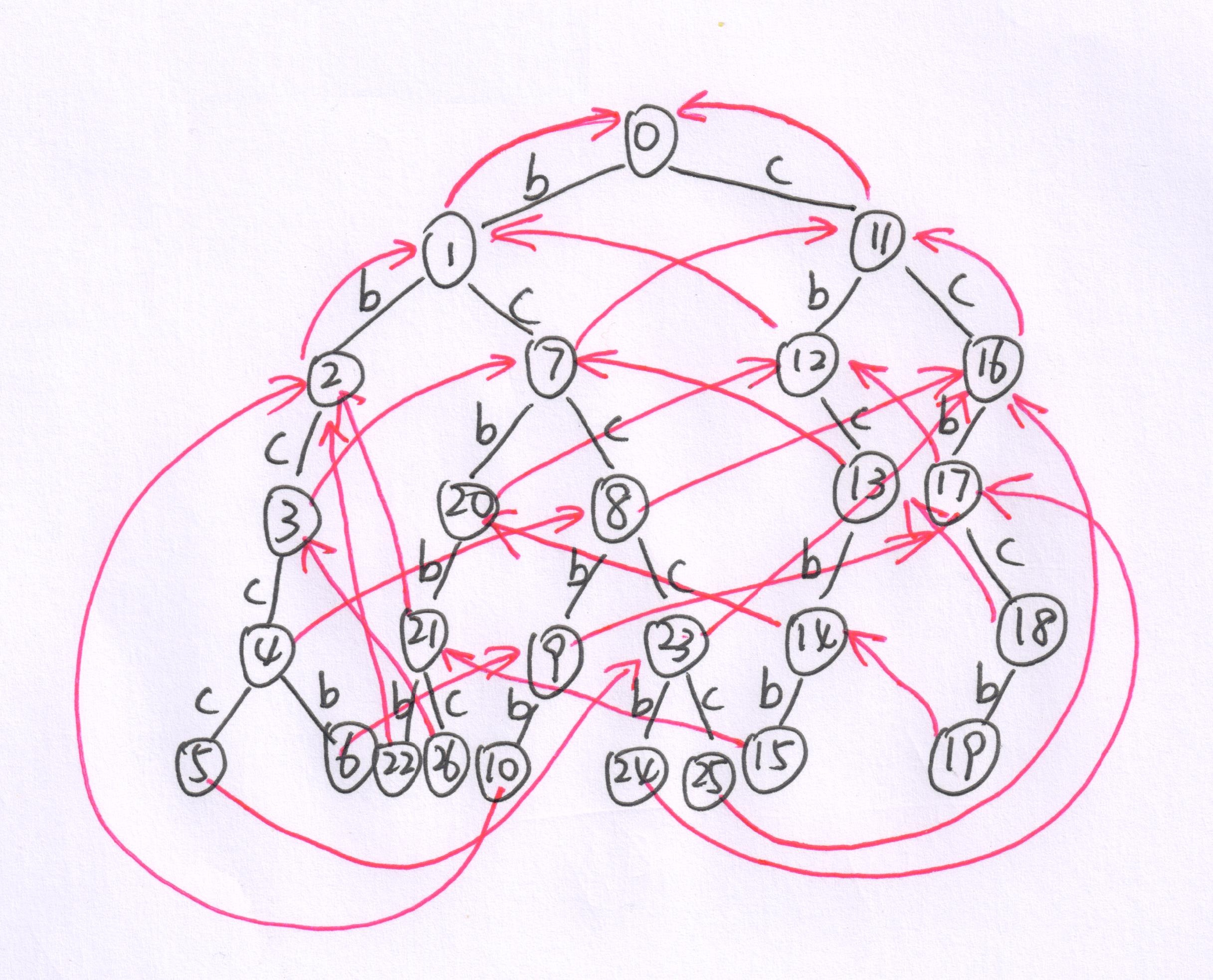
朴素的AC自动机就长这样了(红色的边代表失配边)。每次匹配字符串时,如果失配,就沿着失配边一直走直到匹配;如果匹配就对当前结点追溯其失配边,找到所有在自动机中的当前匹配到的字符串的后缀(因为它们本不会被计入答案)。
对于上面的例子,匹配时访问的结点顺序为:1,7,8,23,24,18,19,15,22,3。由于与KMP算法一样,至多回溯O(m)次,因此保证了复杂度是线性的O(n+m)。
事实上,AC自动机有一些优化的方法:
1.既然每次匹配时我要沿失配边找sum不为0的结点(即存在自动机中的完整字符串,而不是字符串的前缀),那么我为什么不直接开一个数组去存这些失配边指向的第一个sum不为0的结点呢?这样明显剩下一些时间。尽管理论上成立,但是我不建议使用这个优化,因为它不仅使AC自动机的代码变得冗长,还不一定有成效(毕竟只是常数优化)。
2.按我上面的介绍,失配与匹配是两种不同的状态,有不同的应对方法,但实际上两者差距并不大,仔细想想我上文的解释:将u视为v的子结点,进行递归求解,也就是说,失配其实就是匹配到了失配边所连接的结点的子结点。两者密不可分,甚至可以通过一些技巧将两者用同样的方法进行处理——只要将建立失配边的过程中,u的c子结点不存在时,ch[u][c]赋值为ch[fail[u]][c]即可。然后匹配时就不需要考虑失配的情况了,统一按匹配的情况进行转移,写起来方便多了。
这道题就是一道AC自动机模板题,除了注意初始化外没有坑,适合上手。
其他题目以后更新。(其实是因为我才学,也只做了一道题)
UPD(2017.12.24):
例题二:UVaLive 4670 Dominating Patterns(鉴于UVaLive的网站很多人上不去,包括我,我就传vjudge的链接了)P.S.这道题在洛谷上有原题,数据可能加强了一点,这里放出传送门。
这题也算是模板题,注意一下模板串可以重复,推荐用map存重复的字符串的编号。还有就是数据范围,哪个是n,哪个是模板串长度要分清(我一开始就在这里RE一次)。