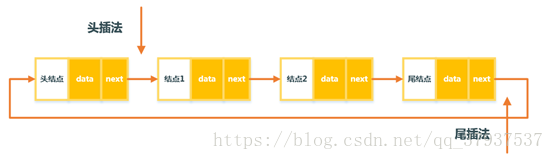
参考:
https://blog.csdn.net/wyqwilliam/article/details/82719058
https://blog.csdn.net/qq_37937537/article/details/80213190
https://blog.csdn.net/qingtian_1993/article/details/81123028
双向链表与循环链表
双向链表
单链表的一个优点是结构简单,但是它也有一个缺点,即在单链表中只能通过一个结点的引用访问其后续结点,而无法直接访问其前驱结点,
要在单链表中找到某个结点的前驱结点,必须从链表的首结点出发依次向后寻找,但是需要Ο(n)时间。
为此我们可以扩展单链表的结点结构,使得通过一个结点的引用,不但能够访问其后续结点,也可以方便的访问其前驱结点。
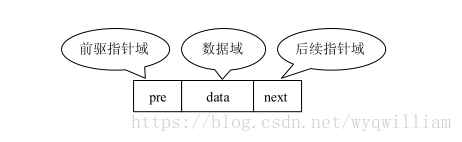
扩展单链表结点结构的方法是,在单链表结点结构中新增加一个域,该域用于指向结点的直接前驱结点。
扩展后的结点结构是构成双向链表的结点结构,如图 所示。
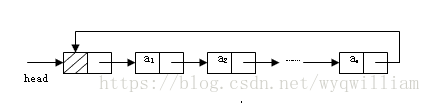
双向链表是通过上述定义的结点使用 pre 以及 next 域依次串联在一起而形成的。一个双向链表的结构如图所示。
在双向链表中同样需要完成数据元素的查找、插入、删除等操作。在双向链表中进行查找与在单链表中类似,只不过在双向链表中查找操作可以从链表的首结点开始,
也可以从尾结点开始,但是需要的时间和在单链表中一样
在使用双向链表实现链接表时,为使编程更加简洁,我们使用带两个哑元结点的双向链表来实现链接表。
其中一个是头结点,另一个是尾结点,它们都不存放数据元素,
头结点的pre 为空,而尾结点的 Next 为空
在具有头尾结点的双向链表中插入和删除结点,无论插入和删除的结点位置在何处,因为首尾结点的存在,插入、删除操作都可以被归结为某个中间结点的插入和删除;
并且因为首尾结点的存在,整个链表永远不会为空,因此在插入和删除结点之后,
也不用考虑链表由空变为非空或由非空变为空的情况下 head 和 tail 的指向问题;从而简化了程序。
Java中的LinkedList底层使用的就是双向链表。
循环链表
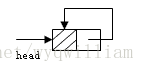
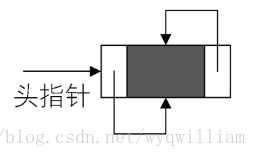
在一个循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。
要转换一个循环链表,你开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点。
循环链表可以被视为"无头无尾"。
循环链表中第一个节点之前就是最后一个节点,反之亦然。
循环链表的无边界使得在这样的链表上设计算法会比普通链表更加容易。
对于新加入的节点应该是在第一个节点之前还是最后一个节点之后可以根据实际要求灵活处理,区别不大。
另外有一种模拟的循环链表,就是在访问到最后一个节点之后的时候,手工跳转到第一个节点。
访问到第一个节点之前的时候也一样。这样也可以实现循环链表的功能,在直接用循环链表比较麻烦或者可能会出现问题的时候可以用。
单向链表的循环带头结点的非空链表
单向链表的循环带头结点的空链表
双向链表的循环带头结点的非空链表
双向链表的循环带头结点的空链表
Java链表的操作--循环链表、双向链表和顺序栈
Java数据结构
1. 循环单链表
对于单链表来说,尾节点的next为空,而循环链表的尾节点的next指向头节点
1. 首先定义内部结点类Entry,包括data和next。
class Entry{
int data;
Entry next;
public Entry(){
this.data = -1;
next = null;
}
public Entry(int data){
this.data = data;
next = null;
}
}
2. 初始化链表,创建一个头节点,next指向自己
public TestClink(){
head = new Entry();
this.head.next = this.head;
}
3. 头插法插入结点
public void headinsert(int val){
Entry tmp = new Entry(val);
tmp.next = head.next;
head.next = tmp;
}
4. 尾插法插入结点
public void tailinsert(int val){
Entry entry = new Entry(val);
Entry tmp = head;
while(tmp.next != head){
tmp = tmp.next;
}
tmp.next = entry;
entry.next = head;
}
5. 删除一个结点
public void delete(int val){
Entry cur;
Entry prev;
cur = head.next;
prev = head;
while(cur != head){
if(cur.data == val){
prev.next = cur.next;
cur = prev.next;
}
cur = cur.next;
prev = prev.next;
}
}
6. 获取链表的长度
public int getlength(){
int len = 0;
Entry tmp = head.next;
while(tmp != head){
len++;
tmp = tmp.next;
}
return len;
}
7. 判断链表是否为空,即判断头节点的next是否为头节点
public boolean isEmpty(){
Entry cur = head;
if(cur.next != head){
return false;
}
return true;
}
8. 测试链表,使用尾插法插入十个节点,并获取链表长度。
public class Test17 {
public static void main(String[] args) {
TestClink tc = new TestClink();
for(int i = 0;i < 10;i++){
tc.tailinsert(i);
}
System.out.println(tc.getlength());
}
}
2. 双向链表
和单链表不同的是,每个数据结点中都有两个指针,分别指向直接后继和直接前驱。单链表只能从头结点开始访问链表中的数据元素,如果需要逆序访问单链表中的数据元素将非常低效。
1. 首先首先定义内部结点类Entry,包括数据域data,指向前一个结点的引用prio和指向下一个结点的引用next。
class Entry{
int data;
Entry next;
Entry prio;
public Entry(){
this.data = -1;
this.next = null;
this.prio = null;
}
public Entry(int val){
this.data = val;
this.next = null;
this.prio = null;
}
}
2. 初始化头结点
DoubleLink(){
head = new Entry();
}
3. 头插法插入结点
public void inserthead(int val){
Entry entry = new Entry(val);
entry.next = head.next;
entry.prio = head;
head.next = entry;
if(entry.next != null){
entry.next.prio = entry;
}
}
4. 尾插法插入结点
public void inserttail(int val){
Entry entry = new Entry(val);
Entry tmp = head;
while(tmp.next != null){
tmp = tmp.next;
}
entry.prio = tmp;
entry.next = null;
tmp.next = entry;
}
5. 删除一个结点
public void deleteEntry(int val){
Entry cur = head.next;
while(cur != null){
if(cur.data == val){
cur.prio.next = cur.next;
if(cur.next != null){
cur.next.prio = cur.prio;
}
}
cur = cur.next;
}
}
6. 测试链表,插入10个结点
public class Test18 {
public static void main(String[] args) {
DoubleLink dl = new DoubleLink();
for(int i = 0;i < 10;i++){
dl.inserttail(i);
}
}
}
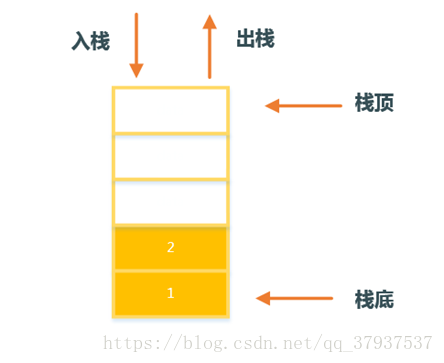
3. 顺序栈
1. 初始化栈
public Stack(){
this(10);
}
public Stack(int size){
this.elem = new int[size];
this.top = 0;
}
2. 判断栈是否满
//栈是否为满
public boolean isFull(){
if(this.top == this.elem.length){
return true;
}
return flase;
}
3. 入栈操作
//入栈
public boolean push(int val){
//判断栈满
if(isFull()){
return false;
}
this.elem[this.top++] = val;
return true;
}
4. 判断栈是否为空
//栈是否为空
public boolean isEmpty(){
return this.top == 0;
}
5. 出栈操作
//出栈
public boolean pop(){
if(isEmpty()){
return false;
}
--top;
return true;
}
6. 获取栈顶元素
//得到栈顶元素
public int gettop(){
if(isEmpty()){
return -1;
}
return this.elem[this.top-1];
}
7. 打印栈内元素
//打印栈内元素
public void show(){
for(int i = 0;i < this.top;i++){
System.out.print(this.elem[i]+" ");
}
System.out.println();
}
8. 测试栈的基本操作
public class test19 {
public static void main(String[] args) {
Stack s1 = new Stack();
for(int i = 0;i < 10;i++){
s1.push(i);
}
s1.show();
s1.pop();
s1.show();
}
}
链表的基本概念以及java实现单链表-循环链表-双向链表
前言
线性结构是非常简单且常用的数据结构,而线性表则是一种非常典型的线性结构。
本节代码传送门,欢迎star:https://github.com/mcrwayfun/java-data-structure
1. 线性表的定义
通常将线性表定义为n个元素的有限的序列,可以表为为 
其中L为表名,a是表中不可再分割的原子数据,亦称为结点或者表项。n是表中表项的个数,也被称为表的长度。当n=0时叫做空表。
线性表的的第一个表项称为表头,最后一个项称为表尾。因为线性表是有序的,这就意味着每个相邻的表项之间都有直接前驱和直接后继的关系,也就是说,除了表头没有直接前驱,其他表项有且仅有一个直接前驱;除了表尾没有直接后继,其他表项有且仅有一个直接后继。
2. 线性表的数据结构
在类库中,java语言包含了一些普通数据结构的实现。该语言的这一部分通常叫做Collections API,表ADT是在Collections API中实现的数据结构之一,看一下其基本的方法:
public interface Collection<AnyType> extends Iterable<AnyType>
{
// 返回表中元素个数
int size();
// 判断表是否为空
boolean isEmpty();
// 清空一张表的数据
void clear();
// 判断表是否含有数据项x
boolean contains(AnyType x);
// 向表中添加一个新的元素x
boolean add(AnyType x);
// 移除表中的元素x
boolean remove(AnyType x);
}3. 链表
链表可以分为有序线性表和无序线性表,本小节仅考虑无序线性表,即链表。链表又分为单链表,环形链表和双向链表。下面将围绕接口Collection中的基本方法实现链表以及完成一些拓展。
3.1 单链表
为了克服顺序表的缺点(新增或删除元素开销大;需要事先分配连续的存储空间),采用链接方式来存储线性表,通常将链接方式存储的线性表成为链表。链表适用于插入或者删除频繁,存储空间需求不定的情形。
3.1.1 单链表的定义
单链表的存储结点包含两部分,一个是数据域(data),用于存储线性表的一个数据元素;一个是指针域(link),用于存放一个指针,该指针指向链表中下一个结点的开始存储地址。用图表示为:

用API可以表示为,其中item为数据域,next为指针域:
class Node<E> {
E item;
Node<E> next;
}- 1
- 2
- 3
- 4
一个线性表的单链表结构可以用下图表示:

其中,单链表的表头可以通过头指针first找到,其他结点的地址则在前驱结点的link域中,表尾结点没有后继,其link域中存放了一个空指针NULL作为终结。因此,要访问单链表中的任一结点,都需要根据头指针first找到第一个结点,再按照各结点link域中存放的指针顺序往下寻找。因此,操作单链表最重要的便是维护一个头指针first
3.1.2 单链表插入和删除
利用单链表来表示线性表,使得插入和删除操作变得非常方便,只需要改变链表结点中的指针值,无需移动表中的元素,就能高效的完成插入和删除操作。现有单链表 
首先来看下单链表的ADT,MyList是一个接口,定义了线性表的基本接口,会放在源码中,这里不作展示
public class SinglyLinkedList<E> implements MyList<E> {
// 表中元素个数
int size = 0;
// 表头指针
Node<E> first;
// 存储结点
private static class Node<E> {
E item;
Node<E> next;
public Node(E item, Node<E> next) {
this.item = item;
this.next = next;
}
}
}插入操作
对于插入算法,需要在数据项ai结点后插入一个新的元素x,那么可能会出现3种情况:
(1) 在表的表头插入一个新结点,那么新结点成为表头,并将first指针指向新结点
// 新结点链向原表头
newNode.next = first;
// 新结点成为表头
first = newNode;- 1
- 2
- 3
- 4
(2) 若ai是链表的最后一个结点,则新结点应追加在表尾。那么新元素成为表尾,且指针域为NULL。定义检测指针cur,需要遍历链表,找到原来的表尾an,新结点则在表尾后插入
// 循环找到表尾last,last指针域指向新结点
cur.next = newNode;- 1
- 2
(3) 若ai即不是表头,也不是表尾。此时,首先让一个检测指针cur指向ai所在的结点,新结点插入到ai所在结点后
// 新结点指针域指向ai的下一个结点
newNode.next = cur.next;
// ai指向新结点
cur.next = newNode;- 1
- 2
- 3
- 4
由上述例子可以得知,在链表中间插入和末尾插入的算法相同,所以可以合并:

综合上述算法,最终可以得到单链表的插入算法:
/**
* 为链表添加一个元素
*
* @param index 指定位置
* @param e 数据
*/
@Override
public void add(int index, E e) {
// 检查index是否越界或数据e是否为空
if (checkPositionIndex(index) || assertDataNull(e)) {
return;
}
Node<E> newNode = new Node<>(e, null);
// 在头结点插入
if (index == 0) {
newNode.next = first;
first = newNode;
} else {
// 在中间和末尾结点插入
// 获取index的前一个数据
Node<E> node = node(index - 1);
newNode.next = node.next;
node.next = newNode;
}
size++;
}拓展,直接向表的末尾添加新结点:
/**
* 在链表尾添加一个元素
*
* @param e
*/
@Override
public void add(E e) {
// 检查数据e是否为空
if (assertDataNull(e)) {
return;
}
Node<E> newNode = new Node<>(e, null);
// 获取当前末尾结点
// 如果头结点不存在则创建
if (isEmpty()) {
first = newNode;
} else {
// 获取到需要添加的头一个
Node<E> node = node(size - 1);
node.next = newNode;
}
size++;
}删除操作
对于删除算法,需要删除指定位置的数据项,那么可能会出现2种情况:
(1) 在链表的第一个结点处删除,即删除链表的第一个结点,那么我们只要将first指针指向下一个结点即可
first = first.next;- 1
(2) 删除链表中间和尾部的结点。假设删除表中第i个结点,让i-1结点的link域保存i+1个结点的地址
// 遍历找到i-1结点,让i-1结点的link域保存i+1个结点的地址
node.next = node.next.next;- 1
- 2

综合上述算法,最终可以得到单链表的删除算法:
/**
* 移除一个指定元素
*
* @param index
*/
@Override
public void remove(int index) {
// 检查index是否越界
if (checkPositionIndex(index)) {
return;
}
// 移除头元素
if (index == 0) {
first = first.next;
} else {
// 移除中间或者尾部元素
// 获取index的前一个数据
Node<E> delNode = node(index - 1);
delNode.next = delNode.next.next;
}
size--;
}3.1.3 单链表的遍历,清空,判空,获取指定结点
遍历操作
/**
* 打印链表
*/
@Override
public void print() {
Node<E> cur = first;
while (cur != null) {
System.out.print(cur.item + " ");
cur = cur.next;
}
System.out.println();
}清空链表操作
遍历链表,清空每个结点的数据项和指针域。头指针first = NULL和size = 0
/**
* 清空链表
*/
@Override
public void clear() {
for (Node<E> x = first; x != null; ) {
Node<E> next = x.next;
x.item = null;
x.next = null;
x = next;
}
first = null;
size = 0;
}
判空操作 /**
* 判断链表是否为空
*
* @return
*/
@Override
public boolean isEmpty() {
return first == null;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
获取指定结点
/**
* 获取指定位置的Node
*
* @param index
* @return
*/
Node<E> node(int index) {
Node<E> x = first;
for (int i = 0; i < index; i++) {
x = x.next;
}
return x;
}3.2 循环链表
在单链表中,如果已知某个结点的地址,想知道该结点的下一个结点地址,那么是非常方便的,所需的时间开销为O(1)。但是想要知道该结点的前驱,就必须从表的最前端开始逐个考查,看谁的后继是指定结点,谁就是该结点的直接前驱,所需时间开销为O(n);另外,在单链表中,已经某个结点,想要寻找其他所有结点,在大多数情况下是不可能的。
为了解决以上这两个问题,出现了单链表的变形,双向链表和循环链表。
3.2.1 循环链表的定义
循环链表本质也是线性表,它的结点结构与单链表的相同。与单链表不同的是,循环链表的表尾结点link域存储不是NULL,而是存储了指向表头指针first的地址。这样,只要知道了表中一个结点的地址,就能遍历表中任何其他的结点。

3.2.2 循环链表的插入和删除
首先来看一下循环链表的ADT,与单链表不同的是,循环链表不仅要维护first,也要维护一个last指针。
public class CircularLinkedList<E> implements MyList<E> {
// 表中元素个数
int size = 0;
// 表头指针
Node<E> first;
// 尾指针
Node<E> last;
// 存储结点
private static class Node<E> {
E item;
Node<E> next;
public Node(E item, Node<E> next) {
this.item = item;
this.next = next;
}
}
}插入操作
对于插入算法,需要在数据项ai结点后插入一个新的元素x,那么可能会出现3种情况:
(1) 需要在表头插入新结点。新结点的link域指向原来的头指针;新结点成为新的头指针;尾指针指向新结点
// 新结点link域指向原来的头指针
newNode.next = first;
// 新结点成为新的头指针
first = newNode;
// 尾指针指向新结点
last = newNode;- 1
- 2
- 3
- 4
- 5
- 6
(2) 在表的末尾插入新结点,新结点的link域指向头指针first;原来的last指针link域指向新结点;尾指针last指向新结点
// 新结点link域指向头指针first
newNode.next = first;
// last指针link域指向新结点
last.next = newNode;
// 尾指针last指向新结点
last = newNode;- 1
- 2
- 3
- 4
- 5
- 6
(3) 在表的中间部分插入新结点。找到插入结点的前一个结点;新结点的link域指向前结点的link域;前结点link域指向新结点;
// 找到插入结点的前结点,假设为node
// 新结点的link域指向前结点的link域
newNode.next = node.next;
// 前结点link域指向新结点
node.next = newNode;- 1
- 2
- 3
- 4
- 5
综上,循环链表的插入算法可以总结为:
/**
* 在链表指定位置新增一个元素
*
* @param index
* @param e
*/
@Override
public void add(int index, E e) {
// 检查index是否越界或数据e是否为空
if (checkPositionIndex(index) || assertDataNull(e)) {
return;
}
Node<E> newNode = new Node<>(e, null);
// 在头结点处插入
if (index == 0) {
newNode.next = first;
first = newNode;
last = newNode;
} else if (index == size - 1) {
// 在尾部插入
newNode.next = first;
last.next = newNode;
last = newNode;
} else {
// 在中部插入
// 获取指定位置前一个元素
Node<E> node = node(index - 1);
newNode.next = node.next;
node.next = newNode;
}
size++;
}拓展,在表的末尾插入新结点:
/**
* 在链表末尾添加元素
*
* @param e
*/
@Override
public void add(E e) {
// 检查数据是否存在
if (assertDataNull(e)) {
return;
}
Node<E> newNode = new Node<>(e, null);
// 头结点不存在
if (isEmpty()) {
first = newNode;
last = newNode;
} else {
last.next = newNode;
newNode.next = first;
last = newNode;
}
size++;
}
删除操作假设要删除循环链表的第i个结点,那么可能会出现3种情况:
(1) 删除表头的结点。表头指针first指向它的link域结点所在的指针;表尾指针last指向新的表头指针;
// 表头指针first指向它的link域结点所在的指针
first = first.next;
// 表尾指针last指向新的表头指针
last = first;- 1
- 2
- 3
- 4
(2) 删除表尾的结点。获取删除位置i的前一个结点,即i-1结点;i-1结点link域指向头指针first;尾指针last指向i-1结点;
// 假设node为i-1结点
// node结点的link域指向头指针
node.next = first;
// 尾指针last指向i-1结点
last = node;- 1
- 2
- 3
- 4
- 5
(3) 删除中间的结点。获取删除位置i的前一个结点,即i-1结点;i-1结点的link域指向i结点的link域指向的指针;
// 假设node尾i-1结点
// i-1结点的link域指向i结点的link域指向的指针
node.next = node.next.next- 1
- 2
- 3
综上,删除的算法可以总结为:
/**
* 移除指定位置的元素
*
* @param index
*/
@Override
public void remove(int index) {
// 检查index是否越界
if (checkPositionIndex(index)) {
return;
}
// 移除头元素
if (index == 0) {
first = first.next;
last = first;
} else if (index == size - 1) {
// 移除尾元素
// 获取移除元素的前一个
Node<E> node = node(index - 1);
node.next = first;
last = node;
} else {
// 移除中间的元素
// 获取移除元素的前一个
Node<E> node = node(index - 1);
node.next = node.next.next;
}
size--;
}3.2.3 循环链表的遍历,清空
获取结点和判空操作与单链表的相同
遍历链表
循环链表的遍历与单链表不一致,因为first指针和last指针指向的是同一个地址,所以需要一些特殊的处理技巧,这里使用do-while循环
/**
* 输出环形链表
*/
@Override
public void print() {
if(isEmpty()){
return;
}
Node<E> cur = first;
do {
System.out.print(cur.item + " ");
cur = cur.next;
} while (cur != first);
System.out.println();
}
清空链表 /**
* 清空链表
*/
@Override
public void clear() {
// 循环清空每个结点
for (Node<E> x = first; x != null; ) {
Node<E> next = x.next;
x.item = null;
x.next = null;
x = next;
}
first = null;
last = null;
size = 0;
}3.3 双向链表
使用双向链表的目的是为了解决在链表中访问直接前驱和直接后继的问题。因为双向链表中每个结点都有两个指针,一个指向结点的直接前驱,一个指向结点的直接后继。这样,无论是向前驱搜索或者向后继方向搜索,其时间开销都是O(1)
3.3.1 双向链表的定义
双向链表的结点结构包含了3个部分,lLink指向它的前驱结点,data为数据域,rLink指向它的后继结点

ADT可以表示为:
class Node<E> {
E item;
Node<E> prev;
Node<E> next;
}3.3.2 双向链表的插入和删除
插入操作
假设在数据项ai的后面插入新结点x,情况可能有3种
(1) 在链表的表头插入一个新结点。新结点的rLink域指向first;first的lLink域指向新结点;first指向新结点;
newNode.next = first;
first.prev = newNode;
first = newNode;- 1
- 2
- 3
(2) 在链表的末尾插入一个新结点。找到链表的末尾结点i-1;i-1的rLink域指向新结点;新结点的lLink域指向i-1结点;
// 假设i-1结点为node
// i-1的rLink域指向新结点
node.next = newNode;
newNode.prev = node;- 1
- 2
- 3
- 4
(3) 在链表的中间插入一个新结点。找到插入位置的前一个结点,即i-1结点;新结点的rLink指向i-1结点的rLink指向的指针;i-1结点的rLink指向的指针的lLink指向新结点;i-1结点的rLink指向新结点;新结点的lLink指向i-1结点;
// 假设i-1结点为node
// 新结点的rLink指向i-1结点的rLink指向的指针
newNode.next = node.next;
// i-1结点的rLink指向的指针的lLink指向新结点
node.next.prev = newNode;
// i-1结点的rLink指向新结点
node.next = newNode;
// 新结点的lLink指向i-1结点
newNode.prev = node;综上,双向链表的插入算法可以总结为:
/**
* 在链表的制定位置添加一个元素
*
* @param index
* @param e
*/
@Override
public void add(int index, E e) {
// 检查index是否越界或数据e是否为空
if (checkPositionIndex(index) || assertDataNull(e)) {
return;
}
Node<E> newNode = new Node<>(e, null, null);
// 表头为空,添加一个头元素
if (index == 0) {
// 表头为空
if (isEmpty()) {
first = newNode;
}
newNode.next = first;
first.prev = newNode;
first = newNode;
} else if (index == size - 1) {
// 在末尾添加
Node<E> node = node(index - 1);
node.next = newNode;
newNode.prev = node;
} else {
// 在中部添加
// 获取添加元素的前一个
Node<E> node = node(index - 1);
newNode.next = node.next;
node.next.prev = newNode;
node.next = newNode;
newNode.prev = node;
}
}删除操作
假设删除第i个位置的数据项,那么有3种情况
(1) 删除表头。表头的rLink域指向的指针的lLink置为NULL;表头指针指向它的rLink指向的指针;
// 表头的rLink域指向的指针的lLink置为NULL
first.next.prev = null;
// 表头指针指向它的rLink指向的指针
first = first.next;- 1
- 2
- 3
- 4
(2) 删除表尾元素。找到删除位置i的前一个结点,即i-1结点;i-1结点的rLink域置为NULL;
// 假设i-1结点为node
// node的rLink域置为NULL
node.next = null;- 1
- 2
- 3
(3) 删除中间元素。找到删除位置i的前一个结点,即i-1结点;
// 假设i-1结点为node
node.next = node.next.next;
node.next.next.prev = node; - 1
- 2
- 3
综上,双向链表的删除算法可以总结为:
/**
* 移除链表中指定位置的元素
*
* @param index
*/
@Override
public void remove(int index) {
// 检查下标是否越界
if (checkPositionIndex(index)) {
return;
}
// 移除头结点
if (index == 0) {
first.next.prev = null;
first = first.next;
} else if (index == size - 1) {
// 移除尾部元素
Node<E> node = node(index - 1);
node.next = null;
} else {
// 移除中部元素
Node<E> node = node(index - 1);
node.next = node.next.next;
node.next.next.prev = node;
}
size--;
}4 总结
通过上述,我们大概了解到了什么是线性表,线性表的代表单链表以及单链表的变形循环链表和双向链表
(1) 单链表:有且仅有一个头结点和一个尾结点。除了头结点,每个结点都有一个直接前驱;除了尾结点,每个结点都有一个直接后继;
(2) 循环链表:循环链表是单链表的变形,其尾结点的link域不为NULL,而是指向头指针first;
(3) 双向链表:双向链表是单链表的变形,其结点结构包含三部分,有lLink,data和rLink;
单链表的优缺点:
优点
(1) 插入和删除方便,只要知道ai结点,那么时间消耗为O(1)
(2) 链式存储结构,无须实现定义存储空间,不必消耗多余的空间
缺点
(1) 查找花费的时间为O(n)
5 附录
本文参考的资料:
- 数据结构(用面向对象方法与C++语言描述)第二版,殷人昆主编
- 图解数据结构——使用java,胡昭民主编
代码传送门,欢迎star:https://github.com/mcrwayfun/java-data-structure