图论算法

最大流最小割问题

最大流问题(maximum flow problem)，一种组合最优化问题，就是要讨论如何充分利用装置的能力，使得运输的流量最大，以取得最好的效果。

在一个连通图中，如果删掉若干条边，使图不联通，则称这些边为此图的一个割集。在这些割集中流量和最小的一个称为最小割。

最大流最小割定理：一个图的最大流等于最小割。

见：https://www.jianshu.com/p/efb2d79e2b0f

概念：

1、容量网络 - 流量网络 = 残留网络

例如：

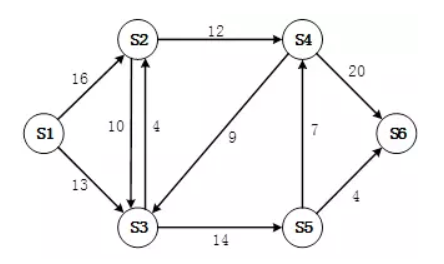
这是一个容量网络（就是每条管道能流多少水）。他的一种可能的流量走向：

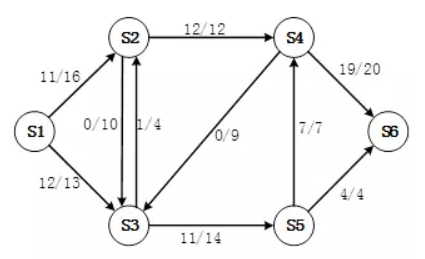
每条边只看斜杠左侧的数值，这些数值构成了流量网络。而残留网络就是每条边斜杠右侧减去斜杠左侧的值得到的网络。其中在残留网络中，S2->S4、S5->S4、S5->S6这些边都不存在了。在最终的残留网络中，是找不到S1->S6的新的增广路径的。

2、反向边

见https://www.jianshu.com/p/efb2d79e2b0f的反向边部分。

1、Ford-Fulkerson算法

Ford-Fulkerson 算法是一种迭代方法。开始时，对所有 u, v ∈ V 有 f(u, v) = 0，即初始状态时流的值为 0。在每次迭代中，可通过寻找一条增广路径来增加流值。增广路径可以看做是从源点 s 到汇点 t 之间的一条路径，沿该路径可以压入更多的流，从而增加流的值。反复进行这一过程，直至增广路径都被找出为止。最大流最小割定理将说明在算法终止时，这一过程可产生出最大流。

优点：会得到一个最小割集，也就是找到了网络中的瓶颈。

缺点：由于增广路经的选择的任意性，导致该算法的时间复杂度不仅依赖于网络规模，还与各边的容量有关。

2、Edmonds-Karp修正算法

"先标号的先扫描"。对已给标号的顶点进行扫描时，先对所有和邻接的未给标号的顶点给予标号。

优点：相对于Ford-Fulkerson算法，其使得流量的增加总是沿着一条长度最短的路径进行流向的。

缺点：时间复杂度相对于标号法减少了，但仍然有很大的时间复杂度。

3、Dinic算法

Dinic算法是标号法的改进算法。Dinic算法兼取以上两种算法，在分层时使用广度优先算法，在寻找增广路径的时候，则采取深度优先策略。是目前三种算法中最高效的一个。

步骤：

1. 初始化流量进行BFS得到层次图。
2. 若汇点不在层次图内，则算法结束。
3. 在层次图内则进行DFS增广。
4. 转到步骤2直至无法增广。

最小费用最大流

背景：最小费用最大流问题是经济学和管理学中的一类典型问题。在一个网络中每段路径都有 "容量" 和 "费用" 两个限制的条件下，此类问题的研究试图寻找出：流量从 A 到 B，如何选择路径、分配经过路径的流量，可以在流量最大的前提下，达到所用的费用最小的要求。如 n 辆卡车要运送物品，从 A 地到 B 地。由于每条路段都有不同的路费要缴纳，每条路能容纳的车的数量有限制，最小费用最大流问题指如何分配卡车的出发路径可以达到费用最低，物品又能全部送到。

实现途径：

1、一条途径是先用最大流算法算出最大流，然后根据边费用，检查是否有可能在流量平衡的前提下通过调整边流量，使总费用得以减少？只要有这个可能，就进行这样的调整。调整后，得到一个新的最大流。然后，在这个新流的基础上继续检查，调整。这样迭代下去，直至无调整可能，便得到最小费用最大流。这一思路的特点是保持问题的可行性（始终保持最大流），向最优推进。

2、另一条解决途径和前面介绍的最大流算法思路相类似，一般首先给出零流作为初始流。这个流的费用为零，当然是最小费用的。然后寻找一条源点至汇点的增流链，但要求这条增流链必须是所有增流链中费用最小的一条。如果能找出增流链，则在增流链上增流，得出新流。将这个流做为初始流看待，继续寻找增流链增流。这样迭代下去，直至找不出增流链，这时的流即为最小费用最大流。这一算法思路的特点是保持解的最优性（每次得到的新流都是费用最小的流），而逐渐向可行解靠近（直至最大流时才是一个可行解）。

第二种办法与前文的 Ford-fulkerson 方法很像，所以选择它更方便，如何找到费用最小的增链流呢？可以用最短路径算法，这里是单源最短路径，所以选择 Dijkstra 算法找出最短路径即可。见：https://github.com/edisonleolhl/DataStructure-Algorithm/blob/master/Graph/MaxFlow/mincostmaxflow.py

最大二分匹配

见：https://blog.csdn.net/smartxxyx/article/details/9672181

其他更深层次的理解见https://blog.csdn.net/smartxxyx/article/details/9275177 这个博友写的系列教程。

图的遍历

深度优先遍历dfs、广度优先遍历bfs。

最短路径算法

需要指定出发点

Dijkstra算法

参见： https://blog.csdn.net/qq_39521554/article/details/79333690

此算法使用了一种'松弛'的思想。算法的结果会把出发点到其他点的所有最短距离都计算出来。

最小生成树

1、Prime算法

算法思想：

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；

3).重复下列操作，直到Vnew = V：

a.在集合E中选取权值最小的边<u, v>（这一步是对Vnew中的点都要进行比较），其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。

2、Kruskal算法

算法思想：先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。

Hungarian Algorithm

最大流算法（用于求二分图最大匹配的时候）的一种改进，用于求最大匹配问题或者指派问题，见：https://blog.csdn.net/u011837761/article/details/52058703

WelshPowell染色算法

不知道怎么用。

Python代码见：https://download.csdn.net/download/qqhanhan/10977626