JAN 的 T3 too hard for me!
P6008 [USACO20JAN]Cave Paintings P
考虑水位不断上涨的过程即每次合并若干个列(点),注意到合并的答案等于 2 者的乘积,并查集维护一下即可。
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define ID(x,y) (((x)-1)*m+(y))
using namespace std;
const int N=1005;
const int mod=(int)(1e9+7);
char e[N][N];
int n,m,tot,fa[N*N],f[N*N];
int fd(int x) {
return x==fa[x]?x:fa[x]=fd(fa[x]);
}
void merge(int x,int y) {
x=fd(x); y=fd(y);
if(x!=y) fa[x]=y,f[y]=f[y]*f[x]%mod;
}
signed main() {
// freopen("6.in","r",stdin);
cin.tie(0); ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) {
cin>>e[i][j];
if(e[i][j]=='.') f[ID(i,j)]=1;
fa[ID(i,j)]=ID(i,j);
}
for(int i=n;i>=1;i--) {
for(int j=1;j<=m;j++) {
if(e[i][j]=='#') continue ;
if(i+1<=n&&e[i+1][j]=='.') merge(ID(i+1,j),ID(i,j));
if(j-1>=1&&e[i][j-1]=='.') merge(ID(i,j-1),ID(i,j));
if(j+1<=m&&e[i][j+1]=='.') merge(ID(i,j+1),ID(i,j));
}
for(int j=1;j<=m;j++) {
if(e[i][j]=='#') continue ;
if(fd(ID(i,j))==ID(i,j)) ++f[ID(i,j)];
}
}
int ans=1;
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(e[i][j]=='#') continue ;
if(fd(ID(i,j))==ID(i,j)) ans=ans*f[ID(i,j)]%mod;
}
}
cout<<ans;
return 0;
}
P6009 [USACO20JAN]Non-Decreasing Subsequences P
类猫树分治,但不需要记录每一层,考虑记起点是啥,上一个是啥,从中间向两边即可。
#include <bits/stdc++.h>
#define ll long long
#define pb push_back
#define ADD(x,y) ((x)+(y)>=mod?(x)+(y)-mod:(x)+(y))
using namespace std;
const int mod=(int)(1e9+7),N=(int)(5e4+5),M=(int)(2e5+5);
vector<pair<int,int> >vec[N];
int a[N],n,m,K,f[N][21][21],g[N][21][21],tmp[N],ans[M],val[N][22],val2[N][22];
void solve(int l,int r) {
if(l==r) return ;
int mid=(l+r)>>1;
solve(l,mid); solve(mid+1,r);
for(int i=l-1;i<=mid+1;i++) {
memset(g[i],0,sizeof(g[i]));
memset(val[i],0,sizeof(val[i]));
}
for(int i=mid;i>=l;i--) {
for(int st=1;st<=K;st++) {
for(int las=1;las<=K;las++) {
g[i][st][las]=g[i+1][st][las];
}
if(st==a[i]) ++g[i][st][a[i]];
for(int j=a[i];j<=K;j++) g[i][st][a[i]]=ADD(g[i][st][a[i]],g[i+1][st][j]);
for(int j=1;j<=K;j++) val[i][st]=ADD(val[i][st],g[i][st][j]);
}
}
for(int i=mid;i<=r+1;i++) {
memset(f[i],0,sizeof(f[i]));
memset(val2[i],0,sizeof(val2[i]));
}
for(int i=mid+1;i<=r;i++) {
for(int st=1;st<=K;st++) {
for(int las=1;las<=K;las++) {
f[i][st][las]=f[i-1][st][las];
}
if(st==a[i]) ++f[i][st][a[i]];
for(int j=1;j<=a[i];j++) f[i][st][a[i]]=ADD(f[i][st][a[i]],f[i-1][st][j]);
for(int j=1;j<=K;j++) val2[i][st]=ADD(val2[i][st],f[i][st][j]);
}
}
for(int i=mid+1;i<=r;i++) {
while(!vec[i].empty()&&vec[i].back().first>=l) {
int qwq=vec[i].back().first,id=vec[i].back().second;
// cout<<l<<" "<<r<<" "<<i<<" "<<qwq<<'\n';
ans[id]=1;
for(int j=1;j<=K;j++)
for(int k=j;k<=K;k++)
ans[id]=ADD(ans[id],1ll*val[qwq][j]*val2[i][k]%mod);
for(int j=1;j<=K;j++) ans[id]=ADD(ans[id],ADD(val[qwq][j],val2[i][j]));
vec[i].pop_back();
}
}
}
signed main() {
// freopen("22.in","r",stdin);
// freopen("xgf.out","w",stdout);
cin.tie(0); ios::sync_with_stdio(false);
cin>>n>>K;
for(int i=1;i<=n;i++) cin>>a[i];
cin>>m;
for(int i=1;i<=m;i++) {
int l,r; cin>>l>>r;
if(l==r) {
ans[i]=2; continue ;
}
vec[r].pb(make_pair(l,i));
}
for(int i=1;i<=n;i++) sort(vec[i].begin(),vec[i].end());
solve(1,n);
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P6142 [USACO20FEB]Delegation P
考虑类似赛道修建,二分,变为判定性问题。不难发现一个点的子树内至多只能剩下一条链,这条链再去与祖先链配对。于是考虑从小到大尝试两两配对(小的能配成功的链比较少,贪心 trick),若非根但当前有奇数条子树链,考虑剩下的一条即可。若有偶数条,其实也有可能一条链单独满了,变为奇数条的情况,因此你加一个 \(0\) 链即可。
注意,根一定要配完!所以倘若是奇数条链的话,必须存在一条自己能满足条件的。
#include <bits/stdc++.h>
//#define int long long
#define pb push_back
using namespace std;
const int N=(int)(1e5+5);
vector<int>g[N];
int n,f[N],Lim;
bool FL;
void dfs(int x,int ff) {
for(int y:g[x]) {
if(y==ff) continue ;
dfs(y,x);
if(!FL) return ;
}
if(!FL) return ;
multiset<int>s; s.clear();
for(int y:g[x]) {
if(y==ff) continue ;
s.insert(f[y]+1);
}
if(s.empty()) return ;
if(x!=1&&((s.size())%2==0)) {
s.insert(0);
}
if(x==1&&(s.size())&1) s.insert(0);
bool ok=1;
while(!s.empty()) {
int qwq=(*s.begin()); s.erase(s.begin());
auto p=s.lower_bound(Lim-qwq);
// cout<<qwq<<" "<<Lim<<'\n';
if(p==s.end()) {
if(ok) {
ok=0; f[x]=qwq; continue ;
} else {
FL=0; break ;
}
} else {
s.erase(p);
}
}
if(x==1&&!s.empty()) {
FL=0; return ;
}
}
bool chk(int x) {
Lim=x; FL=1;
dfs(1,0);
return FL;
}
signed main() {
// cin.tie(0); ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<n;i++) {
int x,y; cin>>x>>y;
g[x].pb(y); g[y].pb(x);
}
int l=1,r=n,res=0;
while(l<=r) {
int mid=(l+r)>>1;
if(chk(mid)) res=mid,l=mid+1;
else r=mid-1;
}
cout<<res;
return 0;
}
P6143 [USACO20FEB]Equilateral Triangles P
很厉害的题!
我一头栽进去转完切比雪夫距离后三角形的形状了。
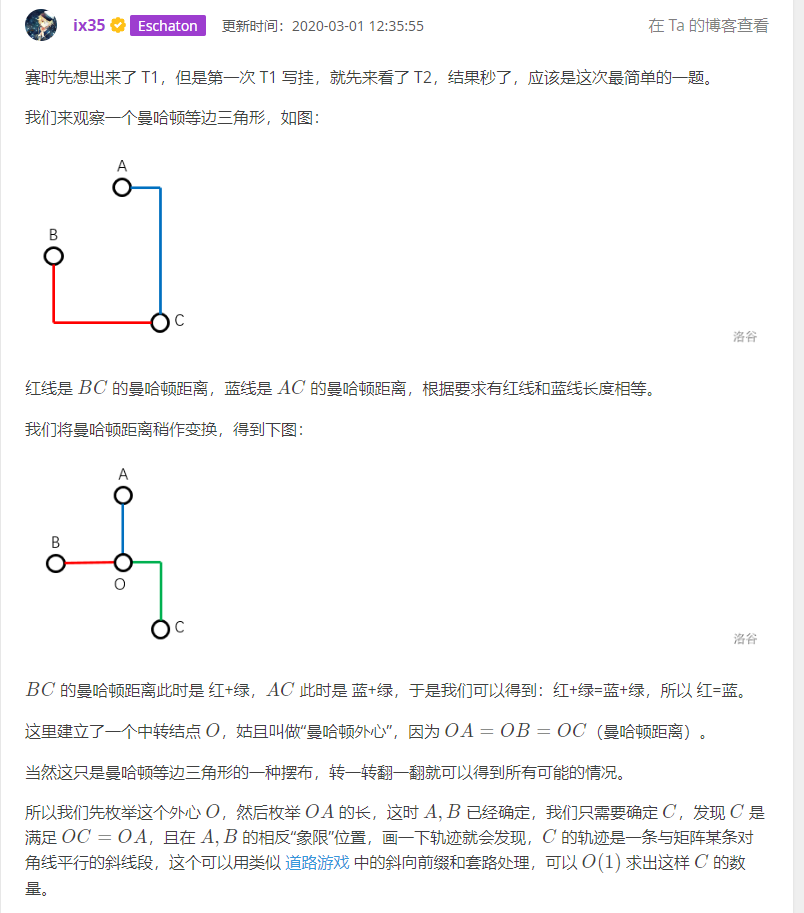
考虑 A,B 所连直线 \(k\) 要么 \(1\) 要么 \(-1\),这是显然的。
你考虑转切比雪夫后画正方形,然后你会发现一定存在 2 个点所连边与 \(x\) 轴或者与 \(y\) 轴平行,然后你旋转 \(\dfrac{\pi}{4}\) 回去显然。
然后就是一个斜向前缀和了,注意下算 "2+1",即这 4 个端点选 2 个组合上一个非端点的,再算 "3" 的。
#include <bits/stdc++.h>
#define pb push_back
#define ll long long
#define int ll
using namespace std;
int a[605][605];
int n;
ll ans,sum1[605][605],sum2[1205][1205],tmp[1205][1205];
void sol1(int x,int y,int l) {
int xx=x-l,yy=y-l;
if(xx<1||yy<1) return ;
if(!a[xx][y]||!a[x][yy]) return ;
// for(int i=1;i<l;i++) {
// int nwy=y+i,nwx=l-i+x;
// if(nwx<1||nwy<1||nwx>n||nwy>n) continue ;
// if(a[nwx][nwy]) ++ans;
// }
// [l-1+x,1+x] [y+1,y+l-1]
// int nwx=x+1,nwy=y+l-1;
// while(nwx<=x+l-1&&nwy>0) {
// ans+=a[nwx][nwy];
// ++nwx; --nwy;
// }
if(1<l) ans+=sum2[x+l-1][y+1]-sum2[x][y+l];
}
void sol2(int x,int y,int l) {
int xx=x-l,yy=y+l;
if(xx<1||yy>n) return ;
if(!a[xx][y]||!a[x][yy]) return ;
if(1<=l-1) {
int dwx=l-(l-1)+x-1,dwy=y-(l-1)-1;
while(dwx<0||dwy<0) ++dwx,++dwy;
if(dwx<0||dwy<0) {
if(dwx<0&&dwy<0) {
int qwq=max(-dwx,-dwy);
dwx+=qwq; dwy+=qwq;
} else if(dwx<0) {
dwy+=-dwx; dwx=0;
} else if(dwy<0) {
dwx+=-dwy; dwy=0;
}
}
ans+=sum1[l-1+x][y-1]-sum1[dwx][dwy];
}
}
void sol3(int x,int y,int l) {
int xx=x+l,yy=y+l;
if(xx>n||yy>n) return ;
if(!a[xx][y]||!a[x][yy]) return ;
// for(int i=1;i<l;i++) {
// int nwy=y-i,nwx=x-l+i;
// if(nwx<1||nwy<1||nwx>n||nwy>n) continue ;
// if(a[nwx][nwy]) ++ans;
// }
// x[x-l+1,x-1] y[y-l+1,y-1]
int nwx=x-l+1,nwy=y-1;
while(nwx<=x-1) {
if(nwx>=0&&nwy>=0) ans+=a[nwx][nwy];
++nwx; --nwy;
}
// if(1<l) {
// cout<<x-1+n<<" "<<y-l+1+n<<" "<<x-l+n<<" "<<y+n<<'\n';
// ans+=sum2[x-1+2*n][y-l+1+2*n]-sum2[x-l+2*n][y+2*n];
// }
}
void sol4(int x,int y,int l) {
int xx=x+l,yy=y-l;
if(xx>n||yy<1) return ;
if(!a[xx][y]||!a[x][yy]) return ;
if(1<=l-1) {
int dwx=x-l,dwy=y;
while(dwx<0||dwy<0) ++dwx,++dwy;
if(dwx<0||dwy<0) {
if(dwx<0&&dwy<0) {
int qwq=max(-dwx,-dwy);
dwx+=qwq; dwy+=qwq;
} else if(dwx<0) {
dwy+=-dwx; dwx=0;
} else if(dwy<0) {
dwx+=-dwy; dwy=0;
}
}
ans+=sum1[x-1][y+l-1]-sum1[dwx][dwy];
}
}
void sol(int x,int y,int xx,int yy,int xxx,int yyy) {
if(x<1||y<1||xx<1||yy<1||x>n||y>n||xx>n||yy>n||xxx<1||yyy<1||xxx>n||yyy>n) return ;
ans+=((a[x][y]&a[xx][yy])&(a[xxx][yyy]));
}
signed main() {
cin.tie(0); ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
char ch; cin>>ch;
if(ch=='*') a[i][j]=1;
}
}
for(int i=1;i<=2*n;i++) {
for(int j=1;j<=2*n;j++) {
sum1[i][j]=sum1[i-1][j-1]+a[i][j];
}
for(int j=2*n;j>=1;j--) {
sum2[i][j]=sum2[i-1][j+1]+a[i][j];
}
}
// for(int i=1;i<=2*n;i++)
// for(int j=1;j<=2*n;j++)
// sum2[i+2*n][j+2*n]=tmp[i][j];
for(int i=1;i<=n;i++) {
for(int j=1;j<=n;j++) {
// if(!a[i][j]) continue ;
for(int k=1;k<=n;k++) {
sol1(i,j,k);
sol2(i,j,k);
sol3(i,j,k);
sol4(i,j,k);
int x=i,y=j;
sol(x-k,y,x,y+k,x+k,y);
sol(x,y+k,x+k,y,x,y-k);
sol(x+k,y,x,y-k,x-k,y);
sol(x,y-k,x-k,y,x,y+k);
}
}
}
cout<<ans;
return 0;
}
P6144 [USACO20FEB]Help Yourself P
学到了,你要让线段以某种顺序加入计算联通线段的段的个数,你可以按 \(l\) 排序,这样子每次加入一定不会合并之前分离的线段段的。
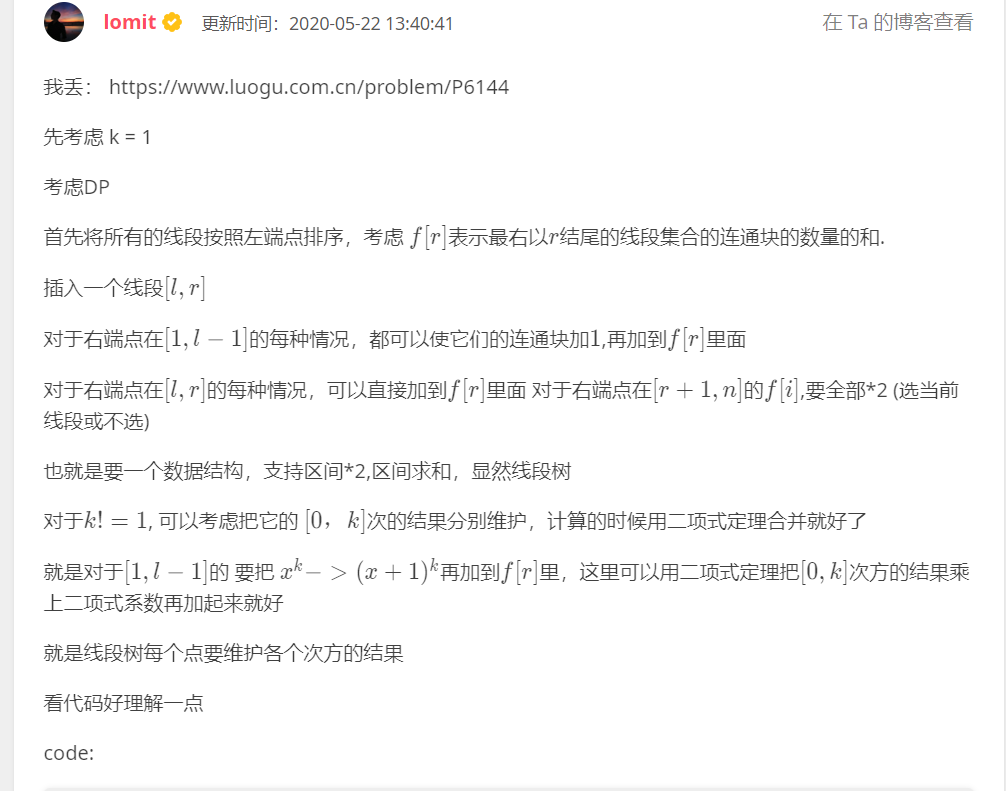
考虑一下为啥直接做二项式定理是对的。
你考虑一个状态的 dp 值可能是 \(\sum_{i\in S} l_i^k\) 的形式的,然后你加 \(1\) 了,那么变为 \(\sum_{i\in S} (l_i+1)^k\),注意一下二项式定理,即 \(\sum_{i\in S} \sum _j \binom{k}{j} l_i^j\),然后你提出去,\(\sum_j \binom{k}{j}\sum_{i\in S}l_i^j\),记 \(f(S,i)\) 为 \(\sum_{x\in S}l_x^i\),则前者变为 \(\sum_j\binom{k}{j}f(S,j)\),所以我们直接对答案做一次二项式定理是对的。综上,你只需要维护这个多项式 \([0,k]\) 次的答案即可。
#include <bits/stdc++.h>
#define pb push_back
#define int long long
#define ADD(x,y) ((x)+(y)>=mod?(x)+(y)-mod:(x)+(y))
using namespace std;
const int mod=(int)(1e9+7);
const int N=(int)(2e5+5);
struct Li {
int l,r;
}p[N];
int n,K,jie[20],djie[20];
struct node {
int a[12];
node() {
memset(a,0,sizeof(a));
}
void clr() {
memset(a,0,sizeof(a));
}
}f[N],g[N];
int C(int n,int m) {
if(n<0||m<0||m>n) return 0;
return jie[n]*djie[m]%mod*djie[n-m]%mod;
}
int fpow(int x,int y) {
int res=1; x%=mod;
while(y) {
if(y&1) res=res*x%mod;
y>>=1; x=x*x%mod;
} return res;
}
node add(const node &x,const node &y) {
node res;
for(int i=0;i<=K;i++) res.a[i]=ADD(x.a[i],y.a[i]);
return res;
}
node add1(const node &x) {
node res;
for(int i=0;i<=K;i++) {
for(int j=0;j<=i;j++) {
res.a[i]=ADD(res.a[i],x.a[j]*C(i,j)%mod);
}
}
return res;
}
node mul(const node &x,int pp) {
node res; int qwq=fpow(2,pp);
for(int i=0;i<=K;i++) res.a[i]=x.a[i]*qwq%mod;
return res;
}
bool cmp(const Li &x,const Li &y) {
return x.l==y.l?x.r<y.r:x.l<y.l; //按 l 是因避免加入后使前面的联通段合并起来
}
#define ls ((cur)<<1)
#define rs ((ls)|1)
node sum[N<<3];
int tag[N<<3];
void push_up(int cur) {
sum[cur]=add(sum[ls],sum[rs]);
}
void build(int cur,int l,int r) {
if(l==r) {
sum[cur]=f[l]; return ;
}
int mid=(l+r)>>1;
build(ls,l,mid); build(rs,mid+1,r);
push_up(cur);
}
void push_down(int cur) {
if(!tag[cur]) return ;
tag[ls]+=tag[cur]; tag[rs]+=tag[cur];
sum[ls]=mul(sum[ls],tag[cur]);
sum[rs]=mul(sum[rs],tag[cur]);
tag[cur]=0;
}
void upt1(int cur,int l,int r,int p,const node &ad) {
if(l==r) {
sum[cur]=add(sum[cur],ad); return ;
}
push_down(cur);
int mid=(l+r)>>1;
if(p<=mid) upt1(ls,l,mid,p,ad);
else upt1(rs,mid+1,r,p,ad);
push_up(cur);
}
void upt2(int cur,int l,int r,int cl,int cr) {
if(cl<=l&&r<=cr) {
++tag[cur]; sum[cur]=mul(sum[cur],1); return ;
}
push_down(cur);
int mid=(l+r)>>1;
if(cl<=mid) upt2(ls,l,mid,cl,cr);
if(cr>mid) upt2(rs,mid+1,r,cl,cr);
push_up(cur);
}
node qry(int cur,int l,int r,int cl,int cr) {
if(cl<=l&&r<=cr) return sum[cur];
push_down(cur);
int mid=(l+r)>>1;
if(cr<=mid) return qry(ls,l,mid,cl,cr);
else if(cl>mid) return qry(rs,mid+1,r,cl,cr);
else return add(qry(ls,l,mid,cl,cr),qry(rs,mid+1,r,cl,cr));
}
signed main() {
cin.tie(0); ios::sync_with_stdio(false);
cin>>n>>K; jie[0]=djie[0]=1;
for(int i=1;i<20;i++) jie[i]=jie[i-1]*i%mod,djie[i]=fpow(jie[i],mod-2);
for(int i=1;i<=n;i++) cin>>p[i].l>>p[i].r;
sort(p+1,p+1+n,cmp);
f[0].a[0]=1; build(1,0,2*n);
for(int i=1;i<=n;i++) {
int l=p[i].l,r=p[i].r;
node qwq;
if(l<=r-1) qwq=qry(1,0,2*n,l,r-1),upt1(1,0,2*n,r,qwq);
if(r+1<=2*n) upt2(1,0,2*n,r+1,2*n);
qwq=qry(1,0,2*n,0,l-1);
qwq=add1(qwq);
upt1(1,0,2*n,r,qwq);
// for(int j=0;j<=2*n;j++) g[j]=f[j],f[j].clr();
// for(int j=l;j<=r;j++) f[r]=add(f[r],g[j]);
// node tmp;
// for(int j=l;j<r;j++) f[j]=g[j];
// for(int j=r+1;j<=2*n;j++) f[j]=mul2(g[j]);
// for(int i=0;i<l;i++) tmp=add(tmp,g[i]),f[i]=g[i];
// tmp=add1(tmp); f[r]=add(f[r],tmp);
}
int ans=0;
for(int i=1;i<=2*n;i++) {
node qwq=qry(1,0,2*n,i,i);
ans=ADD(ans,qwq.a[K]);
}
cout<<ans;
return 0;
}