近似方案-忽略所有条件判断,认为所有分支都能到达
对停机问题分析,

此时还是分不出来到底是否停机。
或者可以将条件抽象为不确定选择。

这种情况下,抽象程序的潜在执行路径是远远超过真实执行路径数量的。(这里条件本身是不会再改变数据的)
为了优化,不在路径末尾做合并,在控制流汇合的所有位置提前做合并(这也是一种近似方案,因为无法保证fv(x)∩fv(y)=fv(x∩y),即数据流不一定满足分配性)
程序可以看成是状态(数据)和状态之间的转移(控制)两部分,因为状态转移的条件都被忽略了,核心分析的部分是状态数据在转移过程中的变化,所以叫做数据流分析。
数据流分析应用示例
给定一个只包含浮点数变量和常量的程序,已知 输入的符号,求输出的符号
比如给定

程序的控制流(这里标红的地方都只是其中一种状态)
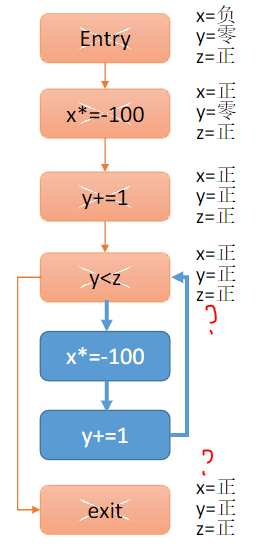
- 该算法安全吗?
- 解:安全,设存在两个不同的解A和B,证明A≥(偏序)B,B≥A,所以A=B。
- 该算法保证终止(terminating)吗?是否会因为环而一直循环?
- 解:保证终止,因为每个点的状态有限,足够遍历
- 该算法一定合流(Confluent)吗?有多个节点可以更新的时候,是否先更新哪个节点不会影响最终结果?
- 解:该算法合流,因为在节点更新的时候,全部需要的状态都列出来了
- Terminating + Confluent = Convergence
活跃变量分析-Liveness Analysis
活跃变量:如果变量在程序位置p之后的执行中还可能会被读取,就称变量在p处活跃。
活跃变量可以从后向前,即callee传给caller直到图中活跃变量稳定,不过要注意必须在callee块传给caller块时别把被重新赋值的变量传给caller。
之后,可以根据活跃变量来删除掉无用赋值或者使用存放非活跃变量的寄存器。
这样写不够形式化:
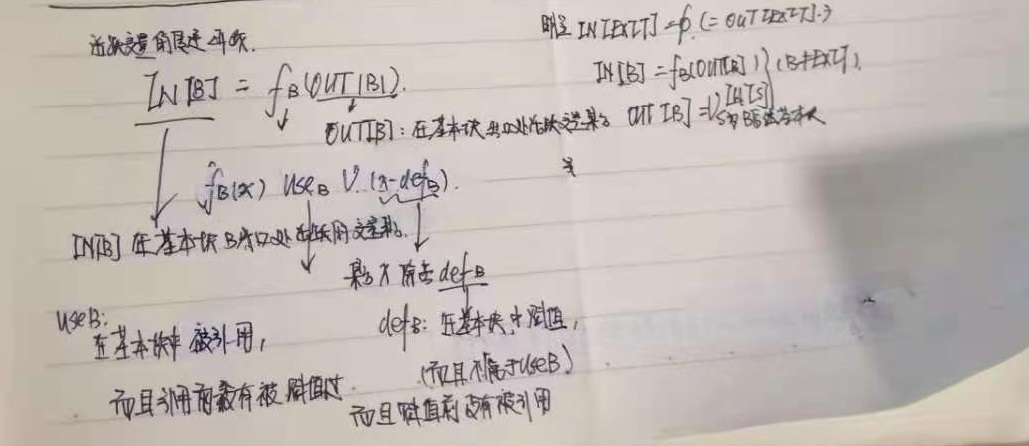
- 该算法安全吗?
- 安全性定义:每个节点最终都能找到对应的全部活跃变量?
- 该算法保证终止(terminating)吗?是否会因为环而一直循环?
- 解:保证终止,因为每个点的状态有限(至少对于示例中的变量数来说),足够遍历
- 该算法一定合流(Confluent)吗?有多个节点可以更新的时候,是否先更新哪个节点不会影响最终结果?
- 解:该算法合流,因为假使有一个活跃变量被遗漏了,之后的算法也会找回这个活跃变量之后才能整张图稳定并且停止
- Terminating + Confluent = Convergence
数据流分析单调框架
- 对所有抽象程序分析方法的通用框架
- 其实算是个bfs+直到图中没有变化 - 目标:通过配置框架的参数,可以导出各种类型 的算法,并保证算法的安全性、终止性、收敛性
- 不同算法在什么地方可能不同?
1. 结点存储的状态可能不同
2. 递推函数可能不同
3. 二者都需要一个统一接口


需要证明的内容:
这里T是半格的最大元,用于初始化节点状态以保障向下推进,MEETv只是子节点状态的一种集合表示,用于计算当前节点状态。
Q: 可以换成succ(entry)吗?
-
如果跑完了之后加一遍全图计算确认,那就可以,图一定是连通的,而且所有的基本块要么是可达的,要么就没有价值无需分析
-
需要证明如下内容
1. 在单条路径上,变换函数保证安全性
2. 交汇函数对多条路径的合并方式保证安全性
3. 交汇函数形成一个半格
4. 半格的高度有限
5. 通常通过结点附加值的定义域为有限集合证明
5. 变换函数均为单调函数
6. 通常定义为(f(D)=(D-KILL)∪GEN)的形式
半格,单调函数


答案是x+y-1,举一个(S_x)极小元(A_x),极大元(T_x),一个(S_y)极小元(A_y),极大元(B_y),则新半格上面的一个极小元会是((A_x, A_y)),极大元((T_x, T_y)),那么此时极大元和极小元距离为(x -1)+(y-1)+1。
注意不要理所当然地认为是(x-1)(y-1)+1
作业
