哈夫曼树

一、树的路径长度

• 两个节点之间的路径长度（PL）是连接两节点的路径上的分支数。如图1中，节点7、8到29的PL都为2，节点15、14到29的PL都为1.
• 树的外部路径长度：各叶节点到根节点的路径长度之和（EPL）。如图1中，叶节点有7、8、14，分别到根节点的路径为2、2、1，那么EPL为5.
• 树的内部路径长度：各非叶节点到根节点的路径长度之和（IPL）。如图1中，非叶节点有15、29，分别到根节点的路径为1、0，那么IPL为1.
• 树的路径长度：PL=EPL+IPL，则PL=5+1=6

图1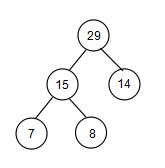：           图2：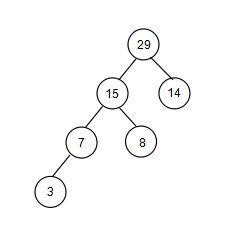

n个节点的二叉树的路径长度不小于下述数列前n项之和（从根节点出发，从左到右编号），即

PL=Σ_i[log₂i]=0+1+1+2+2+2+2+3+3+3+3+3+3+3+3+4+…（[log₂i]取整数）

其路径长度最小者为 PL=Σ_i[log₂i]，只有完全二叉树满足才要求PL=Σ_i[log₂i]

图1为完全二叉树，图2不是完全二叉树，其PL 大于 Σ_i[log₂i]。

二、带权路径长度

很多应用问题中为树的叶节点赋予一个权值，用于表示出现频度、概率值等。因此，在问题处理中把叶节点定义得不同于非叶节点，把叶节点看作“外节点”，非叶节点看作“内节点”。这样的二叉树称为扩充二叉树。

扩充二叉树中只有度为2的内节点和度为0的外节点。根据完全二叉树的性质，有n个外节点就有n-1个内节点，总节点数为2n-1.

若一颗扩充二叉树有n个外节点，第i个外节点的权值为w_i，它到根的路径长度为l_i，则该外节点到根的带权路径长度为w_i*l_i。

扩充二叉树的带权路径长度：树的各外节点到根的带权路径长度之和，即WPL=Σ_i(w_i*l_i)

对于同样的一组权值，放在外节点上，树的组织方式不同，带权路径长度也不同。

如图1：WPL=15*1+14*1+7*2+8*2，如何使得扩充二叉树的带权路径长度最小，当权值大的值离根近，权值小的离根远，则最小。

Huffman树

在带权路径长度达到最小的扩充二叉树即为Huffman树。在Huffman树中，权值大的节点离根最近。

哈夫曼树的构造算法：

1）由给定的n个权值{w₀,w₁,w₂……w_n-1}，构造具有n颗扩充二叉树的森林F={F₀,F₁,F₂……F_n-1}，其中每颗扩充二叉树T_i只有一个带权值w_i的根节点，其左右子树均为空。

2）重复以下步骤，直到F中仅剩一颗树为止：

• 在F中选取两颗根节点的权值最小的扩充二叉树，作为左、右子树构造一颗新的二叉树。置新的二叉树的根节点的权值为其左、右子树上根节点的权值之和。
• 把F中删去这两颗二叉树
• 把新的二叉树加入F