SoftMax函数:
又称归一化指数函数,是逻辑函数的一种推广,它能将一个含任意实数的K维的向量z的“压缩”到另一个K维实向量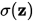 ,使得每一个元素的范围都在 ( 0 , 1 ) {displaystyle (0,1)}
,使得每一个元素的范围都在 ( 0 , 1 ) {displaystyle (0,1)}  之间,并且所有元素的和为1。(0,1)之间,并且所有元素的和为1。
之间,并且所有元素的和为1。(0,1)之间,并且所有元素的和为1。
 for j = 1, …, K.
for j = 1, …, K.
事例:
输入向量[1,2,3,4,1,2,3]对应的Softmax函数的值为[0.0.24,0.064,0.175,0.475,0.024,0.064,0.175]。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
[ 1 , 2 , 3 , 4 , 1 , 2 , 3 ] {displaystyle [1,2,3,4,1,2,3]} ![{displaystyle [1,2,3,4,1,2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d068344b5d5265343f7fdf213e30f73afe408278) 对应的Softmax函数的值为 [ 0.024 , 0.064 , 0.175 , 0.475 , 0.024 , 0.064 , 0.175 ] {displaystyle [0.024,0.064,0.175,0.475,0.024,0.064,0.175]}
对应的Softmax函数的值为 [ 0.024 , 0.064 , 0.175 , 0.475 , 0.024 , 0.064 , 0.175 ] {displaystyle [0.024,0.064,0.175,0.475,0.024,0.064,0.175]} ![{displaystyle [0.024,0.064,0.175,0.475,0.024,0.064,0.175]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9679f3b44ebb0dbf20990e3d86b29b33e57c564) 。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
神经网络计算中的应用:
在人工神经网络最后一层经常试用softmax函数作为分类函数,这些神经网络通常取对数损失函数或交叉熵损失函数,给出了多项Logistic回归的非线性变量。
从 softmax 层得到的输出可以看做是一个概率分布。
softmax在神经网络中
z {displaystyle mathbf {z} }  的“压缩”到另一个K维实向量 σ ( z ) {displaystyle sigma (mathbf {z} )}
的“压缩”到另一个K维实向量 σ ( z ) {displaystyle sigma (mathbf {z} )}  中,使得每一个元素的范围都在 ( 0 , 1 ) {displaystyle (0,1)}
中,使得每一个元素的范围都在 ( 0 , 1 ) {displaystyle (0,1)}  之间,并且所有元素的和为1。
之间,并且所有元素的和为1。
![]() ,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。
,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。 for j = 1, …, K.
for j = 1, …, K. 之间,并且所有元素的和为1。
之间,并且所有元素的和为1。![{displaystyle [1,2,3,4,1,2,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d068344b5d5265343f7fdf213e30f73afe408278) 对应的Softmax函数的值为
对应的Softmax函数的值为![{displaystyle [0.024,0.064,0.175,0.475,0.024,0.064,0.175]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9679f3b44ebb0dbf20990e3d86b29b33e57c564) 。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
。输出向量中拥有最大权重的项对应着输入向量中的最大值“4”。这也显示了这个函数通常的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。 的“压缩”到另一个K维实向量
的“压缩”到另一个K维实向量  中,使得每一个元素的范围都在
中,使得每一个元素的范围都在