前言
在浅谈分词算法(1)分词中的基本问题中我们探讨了分词中的基本问题,也提到了基于词典的分词方法。基于词典的分词方法是一种比较传统的方式,这类分词方法有很多,如:正向最大匹配(forward maximum matching method, FMM)、逆向最大匹配(backward maximum matching method,BMM)、双向扫描法、逐词遍历法、N-最短路径方法以及基于词的n-gram语法模型的分词方法等等。对于这类方法,词典的整理选择在其中占到了很重要的作用,本文主要介绍下基于n-gram的分词方法,这类方法在平时的分词工具中比较常见,而且性能也较好。
目录
浅谈分词算法(1)分词中的基本问题
浅谈分词算法(2)基于词典的分词方法
浅谈分词算法(3)基于字的分词方法(HMM)
浅谈分词算法(4)基于字的分词方法(CRF)
浅谈分词算法(5)基于字的分词方法(LSTM)
基本原理
贝叶斯公式
提到基于N-Gram的概率分词方法,首先我们就要说下伟大的贝叶斯理论,说到贝叶斯理论,先说贝叶斯公式:
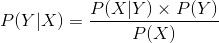
贝叶斯公式也是概率论当中的基础,这里我们不再赘述,推荐一篇文章数学之美番外篇:平凡而又神奇的贝叶斯方法,讲的很不错。下面我们主要关注下在分词当中怎么利用贝叶斯原理。
分词中的贝叶斯
我们知道通常P(Y)是一个常数,所以在使用贝叶斯公式的时候我们更多用如下的公式:
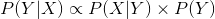
当贝叶斯理论应用在离散数据集上的时候,可以使用频率作为概率来进行计算,在分词算法中,在给定训练语料库中,我们以词为单位进行统计,统计出每个词出现的频率,当出现一句待切分的句子时,我们将所有可能的分词结果统计出来,计算概率最大的作为切分结果。用形式化的语言描述下:
假设训练数据集为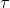 ,其中词典集为D,
,其中词典集为D,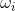 为长度N的句子中的第i个词,那么一句话的联合概率可以表示为:
为长度N的句子中的第i个词,那么一句话的联合概率可以表示为:
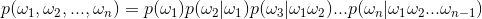
也就是说句子当中的每个词的概率都是一个依赖于其前面所有词的条件概率。说到这里我们就是惯用套路,显然这东东没法计算,那怎么办呢,那就是贝叶斯理论中常用的,做些条件独立假设呗,这也就是所谓n-gram中n的由来。
- 1-gram(unigram), 一元模型,句子中的每个词都是相互独立的,那么上面的公式可以简化如下:
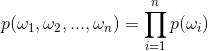
- 2-gram(bigram),二元模型,句子中的每个词仅仅依赖于其前面的一个词:
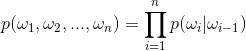
- 3-gram(trigram),三元模型,句子中的每个词依赖于其前面两个词:
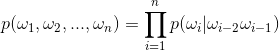
一般来说,我们最多只看到前两个词,有研究表明,大于4个以上的模型并不会取得更好的效果(显然n越大,我们需要找寻n元组的词出现的频率就越低,会很直接的导致数据稀疏问题),通常情况下我们使用的是2-gram模型居多。
2-gram分词举例
假设待切分语句为:“研究生物学”,我们要怎样进行切分呢,直观的讲我们可以看出就这么一句简单的话包含了“研究”、“研究生”、“生物”、“生物学”多个词语,那么直观上我们有如下几种切分方式:
- 研究/生物学
- 研究生/物/学
- 研究/生物/学
- 研/究/生/物/学
我们将这些切法构建为一幅有向无环图,结点为词语,边为条件概率
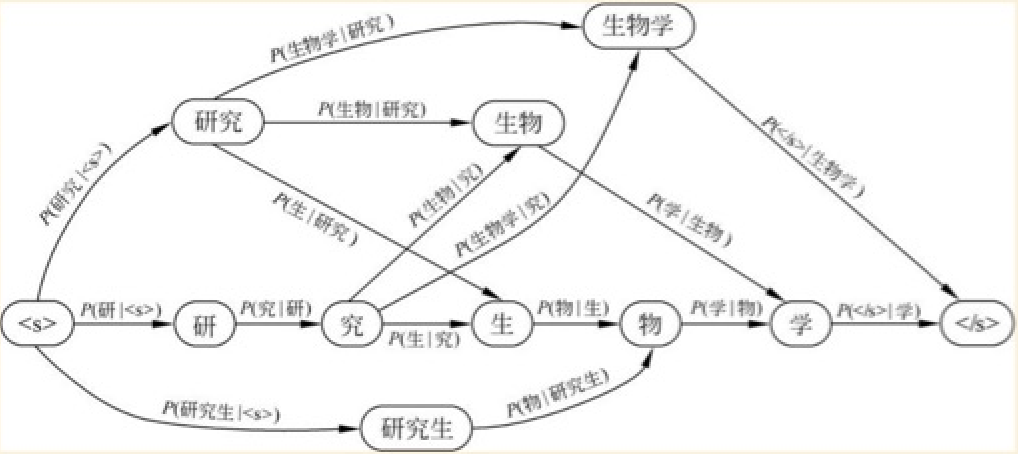
(摘自[4])
那么根据最大似然原理,我们分词的过程转为了在图中求解最佳路径的问题,我们只需要选取任意一种搜索算法,例如在结巴分词中是利用动态规划找寻最大概率路径。
1-gram实例
上面说了那么多,还是上code比较有干货,我们以1-gram为例,来进行一个阐述,这里我们主要参考了结巴分词。在实现的过程中涉及到的核心问题:建立前缀字典树、根据句子建立DAG(有向无环图)、利用动态规划得到最大概率路径。
建立前缀字典树
代码如下:
with open(dict_path, "rb") as f:
count = 0
for line in f:
try:
line = line.strip().decode('utf-8')
word, freq = line.split()[:2]
freq = int(freq)
self.wfreq[word] = freq
for idx in range(len(word)):
wfrag = word[:idx + 1]
if wfrag not in self.wfreq:
self.wfreq[wfrag] = 0 # trie: record char in word path
self.total += freq
count += 1
except Exception as e:
print("%s add error!" % line)
print(e)
continue
我们利用dict来建立这颗前缀字典树,遇到一个词时,会将词路径当中所有的子串都记录在字典树中。(其实这种方式存放是有大量冗余子串的,不过查询是会更加方便)
建立DAG
代码如下:
def get_DAG(self, sentence):
DAG = {}
N = len(sentence)
for k in range(N):
tmplist = []
i = k
frag = sentence[k]
while i < N and frag in self.wfreq:
if self.wfreq[frag]:
tmplist.append(i)
i += 1
frag = sentence[k:i + 1]
if not tmplist:
tmplist.append(k)
DAG[k] = tmplist
return DAG
因为在载入词典的时候已经将word和word的所有前缀加入了词典,所以一旦frag not in wfreq,即可以断定frag和以frag为前缀的词不在词典里,可以跳出循环。
利用动态规划得到最大概率路径
值得注意的是,DAG的每个结点,都是带权的,对于在词典里面的词语,其权重为其词频,即wfreq[word]。我们要求得route = (w1, w2, w3 ,.., wn),使得Σweight(wi)最大。
动态规划求解法
满足dp的条件有两个
- 重复子问题
- 最优子结构
我们来分析最大概率路径问题。
重复子问题
对于结点Wi和其可能存在的多个后继Wj和Wk,有:
- 任意通过Wi到达Wj的路径的权重为该路径通过Wi的路径权重加上Wj的权重{Ri->j} = {Ri + weight(j)} ;
- 任意通过Wi到达Wk的路径的权重为该路径通过Wi的路径权重加上Wk的权重{Ri->k} = {Ri + weight(k)} ;
最优子结构
对于整个句子的最优路径Rmax和一个末端节点Wx,对于其可能存在的多个前驱Wi,Wj,Wk…,设到达Wi,Wj,Wk的最大路径分别为Rmaxi,Rmaxj,Rmaxk,有:
Rmax = max(Rmaxi,Rmaxj,Rmaxk…) + weight(Wx)
于是问题转化为:
求Rmaxi, Rmaxj, Rmaxk…
组成了最优子结构,子结构里面的最优解是全局的最优解的一部分。
很容易写出其状态转移方程:
Rmax = max{(Rmaxi,Rmaxj,Rmaxk…) + weight(Wx)}
代码
代码如下:
def get_route(self, DAG, sentence, route):
N = len(sentence)
route[N] = (0, 0)
logtotal = log(self.total)
for idx in range(N - 1, -1, -1):
route[idx] = max((log(self.wfreq.get(sentence[idx:x + 1]) or 1) -
logtotal + route[x + 1][0], x) for x in DAG[idx])
这里值得注意的是在求频率时,使用了log函数,将除法变成了减法,防止溢出。
完整代码
对于句子“我是中国人”,我们可以看到如下图所示的效果:

我将完整的代码放在了git上,这里的词典用的就是结巴分词中的词典,其中好多代码都是从结巴分词复用过来的,大家需要可以瞅瞅:
https://github.com/xlturing/machine-learning-journey/tree/master/seg_ngram