作者：桂。
时间：2017-05-12 12:45:57
链接：http://www.cnblogs.com/xingshansi/p/6770062.html
前言
主要是最大熵模型（Maximum entropy model）的学习记录。
一、基本性质
在啥也不知道的时候，没有什么假设以及先验作为支撑，我们认为事件等可能发生，不确定性最大。反过来，所有可能性当中，不确定性最大的模型最好。熵是衡量不确定性（也就是信息量）的度量方式，这就引出了最大熵模型：
实际情况里，概率的取值可能不是任意值，因此通常有一些约束条件。
二、理论模型
对于给定的训练数据集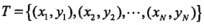
以及特征函数
，最大熵模型的参数求解，对应优化问题：
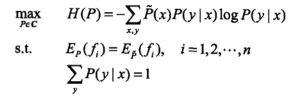
补充：这里多说两句，对于优化问题（且含有不等式约束）的求解，可以将约束条件写成拉格朗日乘子的形式。这样就实现了约束问题→无约束问题的转化。
转化之后的无约束问题，是不是一定有最优解呢？可以求出最优解有一个必要条件，这个条件就是有名的：KKT条件。之前分析过，不细说了。
上面的优化问题可以改变一下形式：
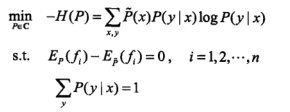
对于这一优化问题，可以利用拉格朗日乘子法（也叫 拉格朗日松弛法）求解：
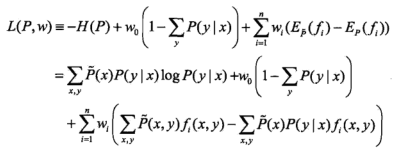
这就将含有约束条件的优化问题转化为不含约束条件的优化问题。对于这个无约束的求解：
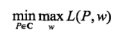
熵是凸函数，且约束条件都是仿射函数，因此该求解的对偶形式求解，二者的结果一致，因此为了简化运算，利用对偶形式求解（这个之前的文章有分析过了）：
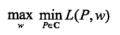
针对对偶问题进行求解，至此完成了参数求解的整个思路，总结一下就是三个步骤：
- 第一步：分析原始问题
- 第二步：拉格朗日乘子法转化
- 第三步：对偶问题求解
三、应用举例
对于A,B,C,D,E，对A的p(y1)及B的p(y2)有约束，求解最大熵模型。
分析（三步走）：
第一步，求解原始问题：
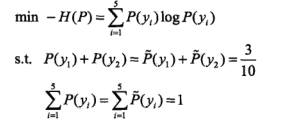
第二步，利用拉格朗日乘子法：
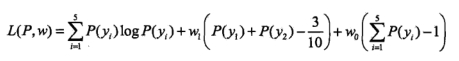
第三步：对偶问题求解：
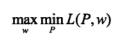
最终结果为：
参考
- 李航《统计学习方法》