剑指OFFER之矩形覆盖（九度OJ1390）

题目描述：

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

输入：

输入可能包含多个测试样例，对于每个测试案例，

输入包括一个整数n(1<=n<=70)，其中n为偶数。

 

输出：

对应每个测试案例，

输出用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有的方法数。

 

样例输入：

4

样例输出：

5

解题思路：

　　观察题目中的矩形，2*n的，是个长条形。本来脑中想象的是复杂的华容道，但是既然只是简单的长条形，那么依然逆向分析。既然是长条形的，那么从后向前，最后一个矩形2*2的，只有两种情况：

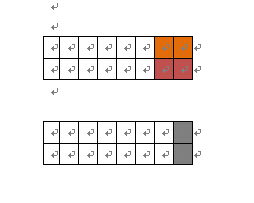
　　 第一种是最后是由一个2*(n-1)的矩形加上一个竖着的2*1的矩形

　　另一种是由一个2*(n-2)的矩形，加上两个横着的2*1的矩形

　　因此我们可以得出，

　　第2*n个矩形的覆盖方法等于第2*(n-1)加上第2*(n-2)的方法。使用代码可以表示为：

for(i=3;i<71;i++){
        arr[i] = arr[i-1]+arr[i-2];
    }

　　仍然要注意数据类型，为long long型

代码：

#include <stdio.h>
long long arr[71] = {0,1,2};
void createArr(void){
    int i;
    for(i=3;i<71;i++){
        arr[i] = arr[i-1]+arr[i-2];
    }
}
int main(void){
    int n;
    createArr();
    while(scanf("%d",&n) != EOF && n>=1 && n<=70){
        printf("%lld
",arr[n]);
    }
    return 0;
}
/**************************************************************
    Problem: 1390
    User: xhalo
    Language: C
    Result: Accepted
    Time:0 ms
    Memory:916 kb
****************************************************************/