发现模式
一个模型实际上都是一个从输入到输出的函数,我们希望用这些模型发现数据中的模式,发现数据中存在的函数依赖,当然前提是数据中本身就存在这样的函数依赖。数据集有很多种类型,可能是有结构的,比如关系数据库中的表,也可能是无结构的,比如文本。我们现在考虑的是一种典型的数据集,这种数据集是一张关系表,每一条记录都代表了一个实体,比如说一朵花,关系表共有很多个字段,但是只有一个字段是标签。表中前n-1个字段是实体的各种特征,最后一个字段是实体的标签,标签是一些离散的值,比如如果一条记录代表一朵梅花,那么它的标签0,如果是一朵兰花,那么它的标签就是1,当然也可以是其他的值。我们用 x 来表示每条记录的前n-1个字段,用 y 来表示每条记录的标签。
现在我们的目标就是希望发现一种模式,也就是从特征到标签的函数依赖关系f,尽可能使得对每条记录有:
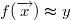
只要函数 f 能够在已知数据集中达到这样的效果,那么我们就相信 f 对于没有出现在数据集中的记录也可以达到这样的效果,也可以满足 f(x) ≈ y,这是一种信念。这种信念没有什么道理可言,也没有办法确定这个观点是否正确,只能单纯的相信这一点。是不是呢?其实我不是很相信这一点 =_=。如果我们相信这一点话,假设现在有一个新纪录,我们就可以利用函数 f 计算出一个函数值,由于函数值和记录的实际标签比较接近,所以这个函数值越接近哪个值,我们就把新纪录的标签判定为哪一个值。把函数 f 的定义域从已知的记录推广到其他记录,这个过程被称为泛化 generalization。
我们要如何使得 f(x) 和 y 足够接近呢?一种方法是使y 和 f(x) 平方差的平均值最小:

E 在这里是平均值的意思,y 每条记录的标签字段,x 是记录的特征字段,分别对每条记录求出 f(x) 和 y 的平方差,再求出平均值,如果平方差的平均值小,就意味着对于大多数记录来说, y 和 f(x) 都比较接近。E 的另一个含义是期望,如果记录很多,那么我们就相信平均值几乎等于期望值,这是统计学的观点。如果 y 和 f(x) 平方差的期望很小,就说明对于大多数记录来说,f(x) 都很接近 y,这就是预测依据。
在直觉上,我们可以把函数 f 的函数值解释成标签的期望。一个实体的标签可以被看成一个离散随机变量,函数 f 根据实体的特征计算出标签的期望值。
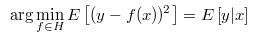
H是一个函数组成的集合,f 是 H 中函数,并且是集合中使得平方差的平均值最小的那一个函数。如果我们真的找到了一个函数 f ,使得对数据集中每条记录,f(x) 和 y 都很接近,函数 f 的函数值可以被解释成一个 “条件期望” ,也就是给定一条记录,知道了特征字段,那么通过函数 f 来得到标签的条件期望值。
神经网络
线性模型和神经网络的原理和目标基本上是一致的,区别体现在于神经网络的中间变量比较多而已。我们考虑一个有四个隐藏层的神经网络,我们希望用这个模型来发现数据库中存在的模式,也就是函数 f 。
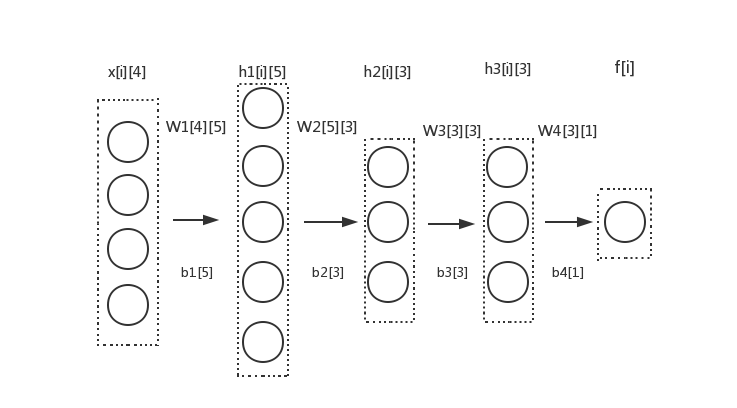
我们设任意相邻的两层都是完全二分图的结构。i 表示数据库中某条记录的编号,对于每一条记录,x[i] 就表示这条记录的特征字段,他们就是模型第一层的输出,f[i] 就表示整个神经网络计算出来的最终输出。有三个隐藏层 h1 和 h2 和 h3,h1[i] 和 h2[i] 和 h3[i] 就表示隐藏层输出,第一个隐藏层有5个输出,第二个隐藏层有3个输出,第三个隐藏层也有三个输出。 W1 ~ W4 都分别是一个矩阵,每个矩阵的第 i 行 j 列的值等于前一层中第 i 个节点到后一层中第 j 个节点的连接权重。比如 W1[0][0] 就可以表示从 x[i][0] 到 h1[i][0] 的连接权重。b1 ~ b4 也是模型的4个参数,称为偏移量,那么后一层输出向量与前一层输出向量之间的关系是:
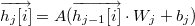
这个公式对应了计算流程的第一阶段:
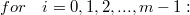
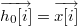

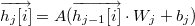



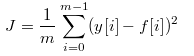
对数据库中的每一条记录,都要执行for循环中的步骤。最开始,线程根据输入层的输出可以得到隐藏层的输出,A是激活函数的意思,比如反正切函数,x[i] 和 h[i] 都是用行向量的形式来表示,更符合数据库中的存储结构。根据第一个层的输出向量,线程计算出第二个层的输出,直到计算出最后一层的输出,也就是 f[i] 。在计算完成每条记录的输出后,线程把模型的输出和记录的标签 y 作比较,计算出平方差平均值 J ,它就是误差。
我画了一幅数据流图,方便分析链式法则的路径。
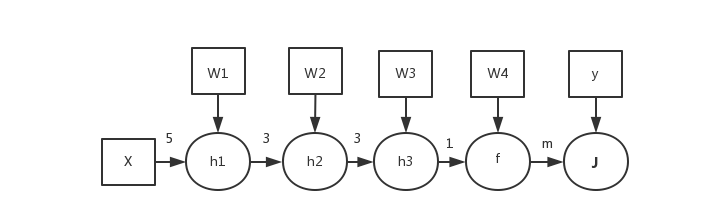
数据流图描述了线程计算出 J 的过程。线程根据记录的特征字段和矩阵 U 计算出向量 h1, h2,h3, 最后计算出模型的输出 f,得出平方差平均值 J 。每个箭头上的数字表示边的数目,比如说数字 5 表示,每个输入层节点的输出可以影响到隐藏层 h1 中 5 个节点输出,同理 3 则表示每个 h1 中的节点,可以影响到 3 个 h2 中的节点输出。这里的 m 则表示线程需要把每条记录的输出 f 都算出来,根据 m 个输出值才能计算出平方差平均值 J,也就相当于从 f 到 J 有 m 条边。比如,从矩阵 U 中的某个元素出发到顶点 J, 一共可以找到 3 × 3 × 1 × m = 9m 条路径。这一点能否理解?
算法的第二个阶段是要求出损失函数对于每个权重的偏导数,就要使用链式法则,就需要两个顶点之间的所有路径。比如说如果我们要求出 J 对 W1[0][0] 的偏导数,我们找到一条路径:
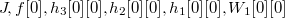
那么这条路径对应的求导链就是:
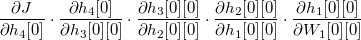
找到所有的路径对应的求导链,并且累加起来,就可以得到 J 对 W1[0]0[0] 的偏导数。相同的做法可以求出损失函数 J 对于每个矩阵偏导数,为了形式上的简洁,把每条记录对应的全部求导链写成矩阵微分的形式:
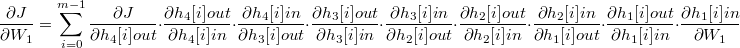
这里的 i 是记录的编号。这个很长的公式对应了算法的第二个阶段:

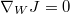
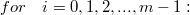


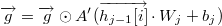
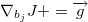
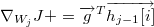
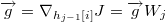


我们的目标就是求出 J 对每个权重W和偏移b的梯度,g 是一个临时变量。可以结合求导链来理解算法的流程,算法中的每个赋值语句和求导链中的每个因子是对应的,在这里都是写成了矩阵微分的形式。for 循环中 g 的初值代表了 J 对最后一层 h4 的输出向量的梯度, 然后计算 h4 的输出向量对 h4 的输入向量的梯度,然后计算 h4 的输入向量对 h3 的输出向量的梯度,并且顺便求出了 J 对 b4 和 W4 的梯度,依此类推,直到遍历整个神经网络。
求出了梯度,就可以使用梯度下降,也就是第三个阶段:
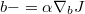
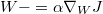
调整权重和偏移量,希望尽可能减小 J 的值。三个阶段循环往复执行很多次,最终的目标就是希望使得对每条记录, f(x) 能够和 y 比较接近。
算法中,如果令 m 等于 1,也就是只用一条记录在训练网络的参数,那么整个算法就变成了随机梯度下降。
regularization
我们修改一下损失函数的形式:
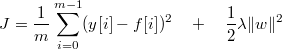
w 表示所有权重组成的向量。损失函数一般都会加上的类似的后缀,这个后缀叫正则项。各种资料中都是这样,算法的不需要太大的改动,但是这个后缀可以使得模型的预测效果更好。
从公式上看,加上这个后缀的目的是希望每个权重矩阵中的值不要太大,否则损失函数就会变得很大;根据我自己的经验,加上这个后缀基本上可以保证权重是收敛的,如果没有这一项,可能会有某些参数会一直不断增大到很大;一般来说,我们希望训练出来的模型不要过分依赖某一维(或几维)的特征,也就是说我们希望每个特征都是有作用的,所以不应该让少数几个参数变得非常大。
还有一种理解,就是说如果一个非线性函数的系数太大,非线性函数对应的曲线一般会非常尖锐,不够平滑,复杂性高,发生过拟合的可能性会比较大。除此之外还有一些先验概率方面的解释,然而我并不明白这里的 “先验” 是什么含义。
交叉熵
我们再一次修改一下损失函数的形式:

依然有一个后缀,不同的是不再使用平方差平均值作为误差评判标准,而是换成了对数函数。算法也不需要太多改动,但我的理解是,使用对数函数可以使模型训练的速度更快,训练效果更好,原因是对数函数的斜率更大。
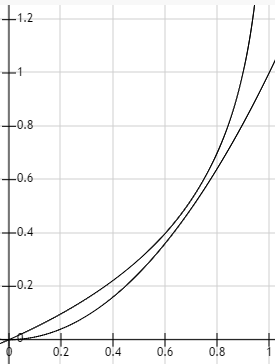
图中两条曲线分别是对数函数和二次函数。横坐标代表预测值和真实标签偏差 |y - f(x)| ,纵坐标是损失函数的值:
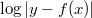
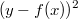
两个函数都随着 y 和 f(x) 的增大而增大,但是对数函数更加陡峭,特别是在偏差比较大的时候。比如初值选得不好导致开始的时候偏差很大对偏差更加敏感,那么使用对数函数就可以求出来很大的梯度,模型就会比较快的收敛到一个比较好的状态。