两道题都是动态规划233。。。
1:

想法:
我们看1 1 0, 我们先计算1 2 3满足1 1个数, 现在有来了一个4要求满足1 1 0;
我们依次将1,2,3,4放在最后一位, 那么前三个数也可以看作一个排列;
1 2 4 :3; (实际排列1 2 4和排列 1 2 3没有区别) 那么当3在最后一位时,我们只要得到
前三位以3(相当于此时的4)结尾的合法数目即可。这样就得到了子问题的结构
状态定义dp[i][j] : (i+1)数字的排列满足前i个要求并以j结尾的合法数目
状态转移: a[i]==1, 则x[i]>x[i+1]。dp[i][j]=sum dp[i-1][k] (j<=k<=i)
a[i]==0, 则x[i]<x[i+1]。dp[i][j]=sum dp[i-1][k] (1<=k<=j-1)
为了进一步优化算法, 定义前缀和sum[i][j]=sum dp[i][k] (1<=k<=j)
时间复杂度O(n), 解决
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const int N=1e3+7; 5 const int mod=1e9+7; 6 LL dp[N][N]; 7 LL sum[N][N]; 8 int a[N]; 9 int n; 10 int main() 11 { 12 cin>>n; 13 for (int i=1;i<n;i++) cin>>a[i]; 14 if (a[1]) { dp[1][1]=1; sum[1][2]=sum[1][1]=1; } 15 else { dp[1][2]=1; sum[1][2]=1; } 16 for (int i=2;i<n;i++) 17 for (int j=1;j<=i+1;j++) { 18 if (a[i]) dp[i][j]=(sum[i-1][i]-sum[i-1][j-1]+mod)%mod; 19 else dp[i][j]=sum[i-1][j-1]; 20 sum[i][j]=(sum[i][j-1]+dp[i][j])%mod; 21 } 22 printf("%lld ", sum[n-1][n]); 23 return 0; 24 }
2:
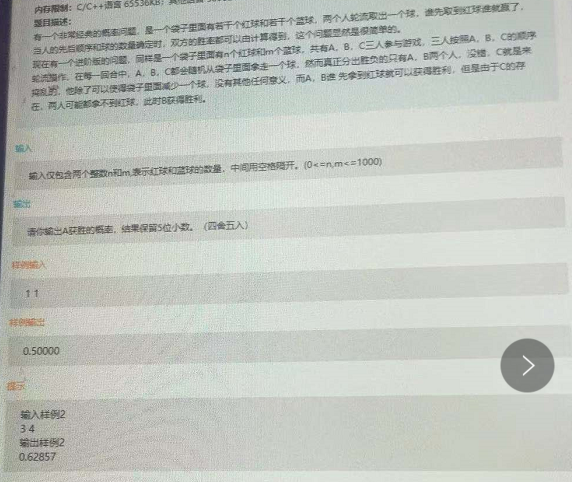
想法: 其实这道题我觉得很easy, 因为数据量并不大。
对于n个红球,m个篮球,A赢的情况有这样3种:
(1)A 先手抽中红球的概率
(2)在A,B都抽中篮球的情况下
2.1 C抽中红球之后A赢的概率
2.2 C抽中篮球之后A赢的概率
每一轮抽中之后,球的数量会减少,这就是一个动态规划问题
状态定义:dp[n][m], n红m蓝 A赢的概率(不会递推, 只会递归。。。233)
