目录
前言
本文只是让读者对博弈论有个初步的了解,能够基本和人“侃大山”。
博弈论正式定义
- The study of mathematical models of conflict and cooperation between intelligent rational(理性的) decision-makers.

博弈分类
- 完全信息静态博弈(static games of complete information)。
- 非完全信息静态博弈(static games of incomplete information)。
- 完全信息动态博弈(dynamic games of complete information)。
- 非完全信息动态博弈(dynamic games of incomplete information)。
解释:
- 完全信息表示所有参与人的 utility function (收益函数)都是公开的,并且所有人都知道收益函数是公开的。而 utility function($S_1 imes cdots imes S_n mapsto Z$) 的大概意思是:每个参与人都各自有一个 utility function,记为 $u_i$(表示第 $i$ 个人的 utility function),当每个参与人都做出一个行动,并形成一个行动序列,记为$(x_1,x_2,cdots,x_n)$($x_i$ 表示第 $i$ 个人的行动),$u_i(x_1,x_2,cdots,x_n)$表示参与人 $i$ 在这个行动序列中的收益(utility or payoff)。
- 非完全信息表示存在一个参与人不知道其他参与人的 utility function,最特殊的情况是被称为 sealed-bid auction(密封报价拍卖),即每个人作出的行动都放在密封的信封中,因此只知道自己的行动,不知道其他人的行动。
- 静态表示每个参与人的行动是同时的,或者说,每个参与人作出行动时并不知道其他参与人所做的行动(想象每个参与人都在不同的房间里,各自把所做的行动写在纸头上,等到所有人都做出行动后,把这些纸头同时拿出房间,这就构成了行动序列)。比如石头剪刀布博弈就是静态的博弈。
- 动态表示每个参与人的行动是序列的,即可能一个参与人是基于某个其他参与人的行动再做行动的。
完全信息静态博弈的标准式描述(Normal-Form Representation)
博弈的英文翻译是 game,在世界上有许许多多的 game,通俗的比如有石头剪刀布、打牌等。那么怎么能够形式化地对这些博弈建模就是“标准式描述”的目的,即标准式描述是对任意一个博弈问题进行精确描述的方法(即任何一个博弈问题都能够转化成标准式描述)。
完全信息静态博弈是最简单的博弈。完全信息静态博弈是由三部分组成:
- 参与人(player)。
- 每个参与人的战略空间(strategy space)。通俗地说就是每个人可以选择的行动的集合。
- 每个参与人的收益函数(utility function)。
因此任何博弈都由这三部分组成,比如石头剪刀布的参与人是两个 players,每个参与人的战略空间是{石头,剪刀,布},收益函数虽不明确但一定存在。
完全信息静态博弈的标准式描述如下:
- 在一个 $n$ 人博弈的标准式描述中,参与人的战略空间为 $S_1,cdots,S_n$,收益函数为 $u_1,cdots,u_n$,我们用 $G={S_1,cdots,S_n~;~u_1,cdots,u_n}$ 表示这个博弈。
也就是说,任何完全信息静态博弈都可以用上面的方式来定义。后面会举一些例子来具体化。
通常我们对于二人博弈这种简单的博弈(仅限于二人博弈),标准式描述可以用双变量矩阵(bi-matrix)表示,比如每个参与人都有两个可选战略,则双变量矩阵如下:
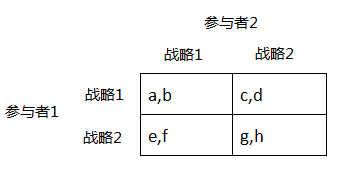
在上图中,每个单元格都有两个数字,前者为参与者 1 的收益,后者为参与者2的收益。比如当参与者 1 选择战略 1,参与者 2 选择战略 1 时,参与者 1 的收益是 a,参与人 2 的收益是 b(其他以此类推)。
特别的博弈
- Constant Sum Game(常和博弈):对于任何战略组合,所有参与者的 utility 之和为常数,即 $forall S=(s_1,cdots,s_n), sum_{i=1}^{n}u_i(s_1,cdots,s_n)=0$。
- Zero Sum Game(零和博弈):他是常和博弈的特例。对于任何战略组合,所有参与者的 utility 之和为0。
纯战略(Pure Strategy)与混合战略(Mixed Strategy)
为了简单起见,这里假设是二人博弈且战略空间大小为2。
- 纯战略:参与者将要做的战略是确定的,比如在某次行动中,参与者将选择战略A。纯战略可以看作是混合战略的一个特例。
- 混合战略:参与者将要做的战略是不确定的,比如在某次行动中,参与者有30%的概率选择战略A,有70%的概率选择战略B,用(0.3,0.7)表示。
下面给出混合战略的正式定义:
- 在$n$个参与人的标准式博弈$G={S_1,cdots,S_n~;~u_1,cdots,u_n}$中,假设$S_i={s_{i1},cdots,s_{iK}}$。那么,参与者 $i$ 的一个混合战略为概率分布 $p_i=(p_{i1},cdots,p_{iK})$,其中对所有 $k=1,cdots,K,0leq p_{ik} leq 1$,且 $p_{i1}+cdots+p_{iK}=1$。
劣战略(Dominated Strategy) 与 优战略(Dominant Strategy)
首先看清楚英语解释,这两个英语解释很容易搞混(dominant 与 dominated)。
劣战略:
- 给定一个博弈的标准式描述 $G={S_1,cdots,S_n~;~u_1,cdots,u_n}$,令 $s_i^{*}$ 是参与者 $i$ 的某个战略,$s_i$ 是参与者 $i$ 的除了 $s_i^{*}$ 的任意战略, 对于其他参与者的任何战略组合 $(s_1,cdots,s_{i-1},s_{i+1},cdots,s_n)$,$u_i(s_1,cdots,s_{i-1},s_i^{*},s_{i+1},cdots,s_n) leq u_i(s_1,cdots,s_{i-1},s_i,s_{i+1},cdots,s_n)$,则称 $s_i^{*}$ 是参与者 $i$ 的劣战略。
- 当 $u_i(s_1,cdots,s_{i-1},s_i^{*},s_{i+1},cdots,s_n) < u_i(s_1,cdots,s_{i-1},s_i,s_{i+1},cdots,s_n)$,则称 $s_i^{*}$ 是参与者 $i$ 的严格劣战略(Strictly Dominated Strategy)。
优战略:
- 给定一个博弈的标准式描述 $G={S_1,cdots,S_n~;~u_1,cdots,u_n}$,令 $s_i^{*}$ 是参与者 $i$ 的某个战略,$s_i$ 是参与者 $i$ 的除了 $s_i^{*}$ 的任意战略, 对于其他参与者的任何战略组合 $(s_1,cdots,s_{i-1},s_{i+1},cdots,s_n)$,$u_i(s_1,cdots,s_{i-1},s_i^{*},s_{i+1},cdots,s_n) geq u_i(s_1,cdots,s_{i-1},s_i,s_{i+1},cdots,s_n)$,则称 $s_i^{*}$ 是参与者 $i$ 的优战略。
- 当 $u_i(s_1,cdots,s_{i-1},s_i^{*},s_{i+1},cdots,s_n) > u_i(s_1,cdots,s_{i-1},s_i,s_{i+1},cdots,s_n)$,则称 $s_i^{*}$ 是参与者 $i$ 的严格优战略(Strictly Dominant Strategy)。
纳什均衡(Nash Equilibrium)和纳什定理(Nash Theorem)
纳什均衡在博弈论中是一个很重要的概念,所谓均衡就是所有人都愿意维持现状(稳定状态的),而不愿意改变行动,因为一旦改变行动就会让自己的收益变差。接下来给出正式定义:
- 在$n$个参与人的标准式博弈$G={S_1,cdots,S_n~;~u_1,cdots,u_n}$中,如果战略组合 ${s_1^{*},cdots,s_n^{*}}$满足对任何一个参与者 $i$,$s_i^{*}$是他针对其他$n-1$个参与者所选战略 ${s_1^{*},cdots,s_{i-1}^{*},s_{i+1}^{*},cdots,s_n^{*}}$的最优战略,则称战略组合 ${s_1^{*},cdots,s_n^{*}}$是该博弈的一个纳什均衡。
对于上面的定义,需要注意几点:
- 此处的战略可能是纯战略或混合战略。
- 一个博弈可能存在多个纳什均衡。
那么可能有人会问,纳什均衡是否一定存在?纳什在1950年提出了“纳什定理”:
- 在$n$个参与人的标准式博弈$G={S_1,cdots,S_n,u_1,cdots,u_n}$中,如果 $n$ 是有限的,且对每个 $i$,$S_i$是有限的,则博弈至少存在一个纳什均衡(此均衡中可能包含混合战略)。
后续文章还会介绍:对称纳什均衡(Symmetric Nash Equilibrium)、本地无嫉妒(Local Envy-freeness)、贝叶斯纳什均衡(Bayesian Nash Equilibrium)。
需要注意几点:
- 如果存在混合战略纳什均衡,则只存在一个。
- 可能不存在纯战略纳什均衡,但存在一个混合战略纳什均衡。
优战略与纳什均衡的关系
- 纳什均衡是针对某个战略组合来说的,即一般说“某个战略组合是纳什均衡的”。
- 优战略是针对某个人的某个战略来说的,即一般说“某个参与人的某个战略是优战略”。
关于纳什均衡与优战略的例子
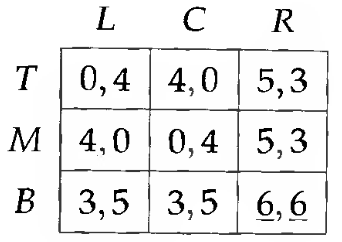
通过对上面图的观察可知:
- (B,R) 是纳什均衡。
- B 不是参与人 1 的优战略,R 也不是参与人 2 的优战略。
例子1:囚徒的困境(Prisoner's Dilemma)
这是一个博弈论经典的例子,我们就这个例子把所有的概念都串一遍。
- 场景:两个犯罪嫌疑人被捕并受指控,但除非一个人招认犯罪,否则警方并不能判刑,警方把他们两个关入不同的牢室(此处体现了这是静态博弈),并对它们说明不能行动带来的后果(此处就体现了这是完全信息博弈)如下面的双变量矩阵所示(Mum表示沉默,Fink表示招认):

首先解释一下上面的图:
- 每个嫌疑犯都有两个可选战略:Mum 和 Fink。
- 当一个嫌疑犯招认,另一个沉默,则沉默者判刑 9 个月(-9),招认者释放(0)。其他的类似。
简单分析:
- 从上图中看出沉默相比于招认是严格劣战略,因为当参与者2选择沉默时,如果参与者1选择沉默,则会判刑1个月,但是如果参与者1选择招认,则会马上释放(0>-1);当参与者2选择招认时,如果参与者1选择沉默,则会判刑9个月,但是如果参与者1选择招认,则会判刑6个月(-6>-9)。因此根据“理性的参与者不会选择严格劣战略”这个假设,此博弈的纳什均衡是(招认,招认)。
解出纳什均衡(利用最优反应函数):
- 首先我们设嫌疑犯1的混合战略为 $(r,1$-$r)$,嫌疑犯2的混合战略为 $(q,1$-$q)$。并设 $r(q)$ 表示嫌疑犯2的混合战略为 $(q,1$-$q)$ 后,嫌疑犯1的最优反应 $(r,1$-$r)$;$q(r)$ 表示嫌疑犯1的混合战略为 $(r,1$-$r)$ 后,嫌疑犯2的最优反应 $(q,1$-$q)$。
- 嫌疑犯1的期望收益:$rq($-$1)+($-$9)r(1$-$q)$-$6(1$-$r)(1$-$q)=r($-$3$-$7q)+15q$-$6$,因为 $q in [0,1]$,因此不管 $q$ 取任何值时,$r$ 取0时嫌疑犯1的期望收益最高。
- 嫌疑犯2的期望收益:$rq($-$1)+($-$9)(1$-$r)q$-$6(1$-$r)(1$-$q)=q($-$3$-$7r)+15r$-$6$,因为 $r in [0,1]$,因此不管 $r$ 取任何值时,$q$ 取0时嫌疑犯2的期望收益最高。
- 综上分析,嫌疑犯1的最优混合战略为(0,1),嫌疑犯2的最优混合战略为(0,1),因此(招认,招认)为纳什均衡。
例子2:石头剪刀布博弈
这个问题太熟悉了,就不介绍规则了,下面给出双变量矩阵:
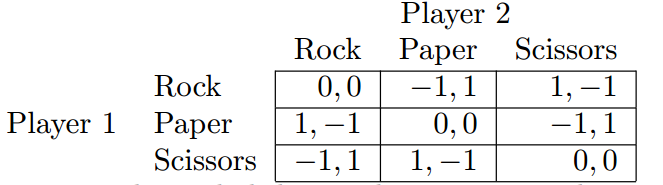
在上图中,如果参与者1选择了布,参与者2选择了石头,则参与者1的 utility 为 1,参与者2的 utility 为 -1,其他类似。
这个游戏肯定是没有纯纳什均衡的,比如,如果参与者1固定出剪刀,参与者2一定会选择出石头去战胜参与者1,而参与者1相应的会选择出布去战胜参与者2,以此循环,因此不存在纯纳什均衡,而由于纳什定理,一定存在一个纳什均衡,因此我们能够确定一定存在混合纳什均衡。
我们利用了如下的定理解出混合策略纳什均衡:
- 在纳什均衡中某个参与者使用混合战略当且仅当此参与者选择任何纯战略的期望收益都相等。
设参与者1的混合战略为 (a,b,1-a-b),参与者2的混合战略为 (c,d,1-c-d)。首先我们求出参与者1的期望收益:
- 当参与者2出石头,则参与者1的期望收益为:b-(1-a-b)=a+2b-1。
- 当参与者2出布,则参与者1的期望收益为:-a+(1-a-b)=1-2a-b。
- 当参与者2出剪刀,则参与者1的期望收益为:a-b。
根据前面提及的定理,我们可得 a+2b-1=1-2a-b=a-b ,求得:$a=1/3,~b=1/3$,同样得$c=1/3,~d=1/3$。
因此混合战略纳什均衡为:$([1/3,1/3,1/3],[1/3,1/3,1/3])$。
参考文献
[1] Gibbons, Robert. Game theory for applied economists. Princeton University Press, 1992.
[2] http://www.znu.ac.ir/members/afsharchim/lectures/MixedStrategy.pdf
拓展读物
[1] 迪克西特, 内勒巴夫, 王尔山. 策略思维: 商界, 政界及日常生活中的策略竞争. 中国人民大学出版社, 2002.
[2] 刘树林, 戎文晋. 搜索引擎广告的机制设计理论与实践. 科学出版社, 2010.