堆是完全二叉树
子树是不相交的
度 节点拥有子树的个数
满二叉树:
每个节点上都有子节点(除了叶子节点)
完全二叉树:
叶子结点在倒数第一层和第二层,最下层的叶子结点集中在树的左部
,在右边的话,左子树不能为空
二叉搜索树:
左边子节点小于父节点,右边子节点大于父节点
堆:
也叫队列,在堆尾插入,在堆头取出
最大堆:
最上边比下边的两个数都大,所有的节点都满足这个规则
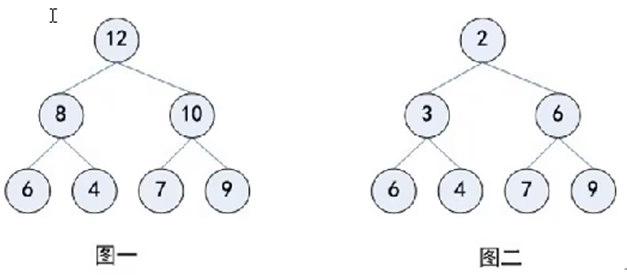
最小堆:
父节点一定比两个子节点要小
特征:
堆起始坐标从1开始
如果用列表表示一个堆:
堆的坐标从1开始算
当前坐标是i
左节点坐标是2i
右节点坐标是2i+1
父节点坐标是i//2 取整
如果想找到最后一个带有子节点的节点坐标:
堆的长度//2
[0,1,2,3,4,5]
[0,1,2,3,4,5,6,7]
1
2 2*1+1=3
2*2 2*2+1=5
0
1 2
3 4 5 6
堆的坐标从0开始算
当前坐标是i
左节点坐标是2i+1
右节点坐标是2i+2
父节点坐标是(i-1)//2 取整
如果想找到最后一个带有子节点的节点:
(堆的长度-1)//2
父节点的位置是K//2,它的左节点是2k,右节点是2k+1
在堆里插入一个元素:上滤
最大堆:
所有的父节点必须大于它的两个子节点
如果将新元素增加到堆的末尾:加一个88
要保证最大堆的规则,新元素和父节点调整交换的操作叫做上滤
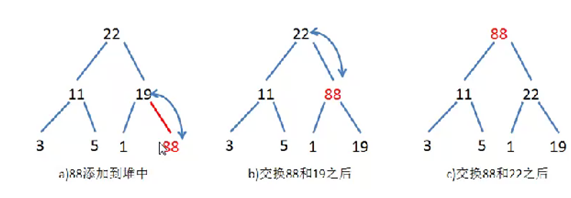
只要插入的节点比父节点小,就不做交换了,不交换那么排序就停止了
当发生了新插入节点和父节点没有交换的情况,那么上滤过程及结束了
删除根元素:下滤
删除堆顶元素,两个子元素比较,大的上去,空出的元素的两个子元素继续比较,大的再上去。。。

最小堆:
所有的父节点必须小于它的两个子节点
堆排序:
算法:一个列表是待排序的
构造最大(小)堆:
最大堆的规则:堆中所有的父节点必须都大于它的子节点
最大堆中的最大值是:根
最小堆的规则:堆中所有的父节点必须都小于它的子节点
最小堆中最小值是:根
排序:
假设使用最大堆
1生成一个空列表存储排序后的结果
2将待排序的list构造成最大堆
3将最大堆的根元素放到空列表中,将剩余的元素通过下滤重新构造最大堆
4然后重复3的步骤,知道所有的元素都当过一次最大堆
拆解过程:
列表中的元素是排好序的,并且是降序的
result =[]
5
3 4
1 2
第一次:result:[5]
3 4
1 2
剩下的元素要构造新的最大堆
4
3
1 2
第二次:result:[5,4]
3
1 2
再次构造最大堆
第三次:result:[5,4,3]
1 2
再次构造最大堆
2
1
第三次:result:[5,4,3 ,2]
1
再次构造最大堆
第四次:result:[5,4,3,2,1]
完成了所有元素当过一次堆的根元素条件,结束堆排序
构造最大堆的时候,如何构造:
从堆的最下层开始构造,每构造一次进行一次上滤
将最大值向上传递。
下滤是从堆顶取值
代码:
# encoding=utf-8
#左叶子、右叶子和父节点,三个元素,找到最大的一个
def maxHeap(heap,heapSize,i):#构造最大堆
#参数heap为一个list,heapsize是指定这个list要操作的长度
#i为某个节点,假设我们传递的是列表的倒数第三个元素
#它的左节点坐标:2i
#那么它的右节点坐标:2i + 1
#它的父节点:i/2
left = 2*i +1
right = 2*i +2
larger = i#当前节点的值
#通过2次if的比较,将left、right和larger三者的最大值找到
#然后将最大值所在的坐标赋值给larger
if left < heapSize and heap[larger] < heap[left]:
larger = left
if right < heapSize and heap[larger] < heap[right]:
larger = right
#以上两步是把三个节点中,最大的值的坐标给了larger
#如果lager的值不是i,说明i的值需要和最大值进行交换
#因为i的坐标是最大堆的堆顶,所以必须是最大值
#如果不是i最大,则说明左结点,或者右节点最大,交换值
#后,说明下面的堆有可能需要进行调整,所以通过递归来
#建立左(右)结点下的最大堆。
#如果最大值就是i,没有进行交换值,所以不需要进行建立
#左(右)结点下的最大堆,这是因为
#做交换,如果最大值的坐标不是当前节点的坐标,说明更大的是左右节点之一
#就把最大那个和当前节点做一个交换,这样最大的就跑到上边去了
if larger != i:
heap[i],heap[larger] = heap[larger],heap[i]
maxHeap(heap,heapSize,larger)#递归调用larger是左节点坐标或者右节点坐标,继续去找下边的最大值,做交换
#如果发生了larger =i 的情况,则次函数调用结束
#以上步骤完成,堆顶坐标为i坐标的最大子堆建立好了
def buildMaxHeap(heap):
#heap参数是未排序、未建堆的list
heapSize = len(heap)
#堆的长度//2可以找到堆里面的
#最后一个带有子节点的节点
#循环可以实现从堆的最下层节点开始建堆
#每次建立的堆都是一个最大堆
#简单来说把所有字段都建成最大堆
#然后组成了最终的最大堆
for i in range((heapSize-1)//2 -1,-1,-1):
maxHeap(heap,heapSize,i)
#(heapSize-1)//2是算出来当前堆中最后一个含有子节点的坐标
'''
5
3 4
2 1 -1
'''
def heapSort(heap):
#先把所有元素先建立一个最大堆
buildMaxHeap(heap)
#将堆中所有的元素都遍历一遍
#让每个元素都做一次堆顶
#然后将堆顶的每个元素都换到堆的最后一个节点
for i in range(len(heap)-1,-1,-1):
heap[0],heap[i] = heap[i],heap[0]
#maxheap中的i是列表的长度,这样可以防止追加到
#堆后面的元素重新被当做最大堆元素进行建队
maxHeap(heap,i,0)
return heap
#第一次循环的时候,把最大值放到了列表最后面
#把最后一个值(肯定不是最大值)放到了堆顶,然后把不包含最后一个元素的
#剩余元素,重新进行最大堆排序
#第二次循环的时候,把堆顶(次大值)放到列表倒数的第二个位置,然后把不包含最后
#两个元素的剩余元素,重新进行建立最大堆
#。。。。
#循环结束,那么列表的数据就排好了
if __name__ == '__main__':
heap1 = [3,4,5,6,23,4,1,1,23,45,6678]
print (heap1)
heapSort(heap1)
print (heap1)
算法:
将一个未排序的list,做成最大堆
buildMaxHeap函数通过maxHeap函数构造了最大堆
第一次从最大堆取出的元素和列表的最后一个的元素交换
位置,我们就找到了最大值
剩余的元素,进行新的最大堆建立
第二次从新建的最大堆堆顶取出来最大值,这个值和
列表中的倒数第二个数进行交换,那么第二大的值就找到了,
此时,最大值在列表的最后,第二大值在列表的倒数
第二个元素
第三次。。。。。重复上面的过程
直到所有的元素都被交换过一次位置
刚才有一个地方讲解有偏差
maxHeap 这个函数的交换逻辑,应该是既不算上滤,也不算下滤
上滤:新插入元素和父节点比对,发生交换。下滤:左右节点比对后发生交换
maxHeap 这个函数的交换逻辑是三个数找到最大的,和上滤下滤还是有一些区别。
for i in range((heapSize-1)//2,-1,-1):
maxHeap(heap,heapSize,i)
这个循环要理解一下:
这个循环调用,表示从最下层的子树,开始实现最大堆,这个就是我刚才说的从最下层开始建立最大堆的过程