一、梯度下降
引入:当我们得到了一个目标函数后,如何进行求解?直接求解吗?(并不一定可以直接求解,线性回归可以当做是一个特例)
梯度:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。在机器学习中一般指的就是目标函数的偏导数。
下降:正常求出来的一个梯度是朝着梯度上升的一个方向,所以梯度下降就是梯度上升的反方向。
基本过程:首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。局部优化达到最大的优化。
常规套路:机器学习的套路就是我交给机器一堆数据,然后告诉它什么样的学习方式是对的(目标函数),然后让它朝着这个方向去做。
如何优化:一口吃不成个胖子,我们要静悄悄的一步步的完成迭代(每次优化一点点,累积起来就是个大成绩了)。
现在假设有这样一个目标函数:
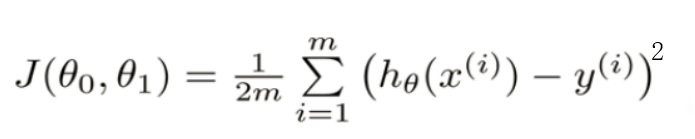

现在我们需要寻找山谷的最低点,也就是我们的目标函数终点(什么样的参数能使得目标函数达到极值点)。
那么下山要分几步走呢?首先随机取一个点
(1):然后找到当前最合适的方向
(2):走那么一小步,走快了该”跌倒 ”了
(3):按照方向与步伐去更新我们的参数,也就是重复一二步。
二、梯度下降策略选择
(1)批量梯度下降:(容易得到最优解,但是由于每次考虑所有样本,速度很慢)
(2)随机梯度下降:(每次找一个样本,迭代速度快,但不一定每次都朝着收敛的方向)
(3)小批量梯度下降法:(每次更新选择一小部分数据来算,实用!)batch
三、学习率
上面提到我们会按照方向去更新参数,那么更新的幅度就叫做步长,一般叫做学习率。
(1)学习率(步长):对结果会产生巨大的影响,一般小一些
(2)如何选择:从小的时候,不行再小
(3)批处理数量:32,64,128都可以,很多时候还得考虑内存和效率
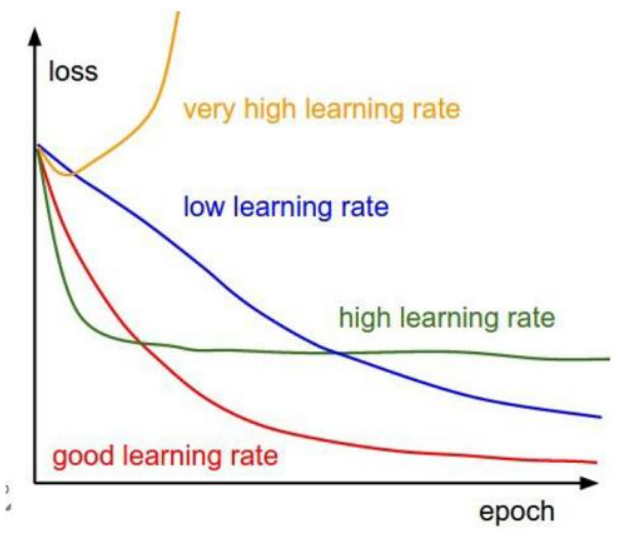
损失函数就是用来表现预测与实际数据的差距程度,loss表示用来表现预测与实际数据的差距,我们的目标就是让loss的值越接近0越好。