P3378 【模板】堆

题解
其实就是一个小根堆啦,STL就可以解决,但是拥有闲情雅致的我学习了Jelly_Goat的左偏树,增加了代码长度,妙啊
Solution 1 STL
STL 里面priority_queue默认是大根堆,修改一下变成小根堆
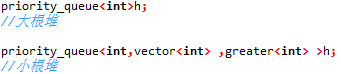
#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<cstdlib> #include<queue> using namespace std; typedef long long ll; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n,opr,x; priority_queue<int,vector<int> ,greater<int> >h; int main() { n=read(); while(n--) { opr=read(); switch(opr) { case 1 : x=read();h.push(x);break; case 2 : printf("%d ",h.top() );break; case 3 : h.pop() ;break; default : break ; } } return 0; }
Solution 2 左偏树
什么是左偏树呢?
就是一个类似二叉堆的东西,画出来像一个二叉树
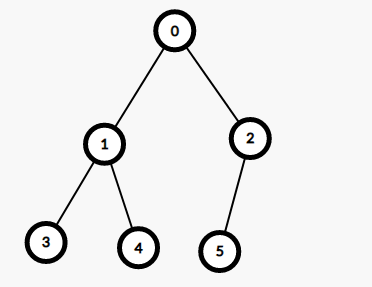
前置芝士:
1.我们定一个节点的 distance 为他距离自己子树中最右边节点的距离,下面简称 dist
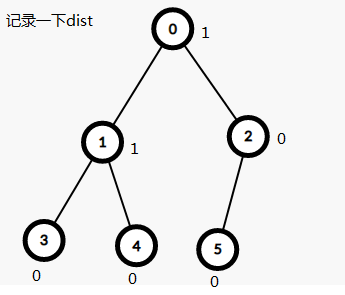
所以,没有右儿子的节点dist就是0啦
2.规定左偏树中,对于一个节点来说,他的左儿子的dist > 他的右儿子的dist
然后这棵树整体就左偏啦
3.怎么计算dist???
dfs跑一遍???
其实也就是 dist [ fa ] = dist [ rson ] + 1
因为得到一个节点的dist一定是与他的右儿子有关的,既然之前知道了右儿子的dist,从右儿子转移过来,也就是dist [ rson ] + 1 ,不就得到自己的dist了吗
支持操作
1.merge 合并操作
我们在用左偏树实现小根堆(大根堆也可以实现)
假设我们要合并两个小左偏树 a,b

(1)如果一个为空,直接返回另一个不就好啦
(2)如果两个都不为空,那么我们就把他们的根节点权值较小的一个作为合并后的根节点,如果两个根节点的权值一样,那么就把dist较大的一个作为新根节点
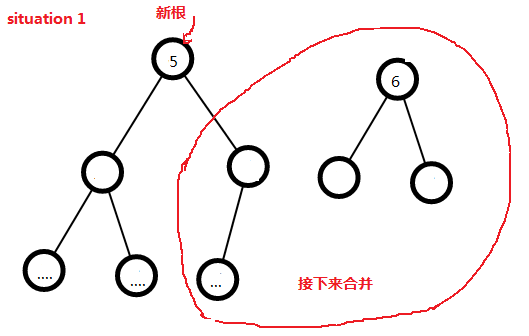
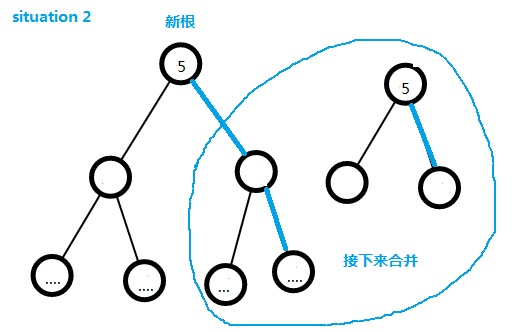
(3)然后继续往下面合并,假设新根是a,那么把b合并到他的右子树去,然后继续处理a的左右子树
(4)get一下新根的dist
2.insert 插入操作
get一个新的点,然后把他与原来的左偏树合并
3.top 访问堆顶 (左偏树实现小/大根堆)
如果堆不为空,就输出堆顶元素,否则输出0
4.pop 弹出堆顶
也就是把左偏树的根节点去掉,合并他的左右子树
5.size 记录一共多少个元素
int cnt 记录,每次新加一个点 就cnt++,弹出一个点,就cnt--
#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<algorithm> #include<cmath> #include<cstdlib> #include<queue> using namespace std; typedef long long ll; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e6+10; struct Heapnode { int lson=0,rson=0,val=0,dist=0; }; struct Heap { Heapnode tree[maxn]; int cnt=0,tot=0,rt=0; inline int New(int val) { ++tot; tree[tot].val=val; return tot; } inline int set_dist(int a) { return tree[a].rson ? tree[tree[a].rson].dist+1 : 0; } int merge(int a,int b) { if(a==0||b==0) return a+b; else if(tree[a].val>tree[b].val) swap(a,b); else if(tree[a].val==tree[b].val&&tree[a].dist<tree[b].dist) swap(a,b); tree[a].rson=merge(tree[a].rson,b); if(tree[a].lson!=0&&tree[a].rson!=0){ if(tree[tree[a].lson].dist<tree[tree[a].rson].dist) swap(tree[a].lson,tree[a].rson); } else if(tree[a].lson==0&&tree[a].rson!=0) swap(tree[a].lson,tree[b].rson); set_dist(a); return a; } inline void insert(int val) { cnt++; int b=New(val); rt=merge(rt,b); } inline int top() { return rt?tree[rt].val:0; } inline void pop() { cnt--; int a=tree[rt].lson,b=tree[rt].rson; rt=merge(a,b); } inline int size() { return cnt; } }h; int n,opr,x; int main() { n=read(); while(n--) { opr=read(); switch(opr) { case 1 : x=read();h.insert(x);break; case 2 : printf("%d ",h.top() );break; case 3 : h.pop() ;break; default : break ; } } return 0; }