背包DP模型
>背包DP
◦一般是给出一些“物品”,每个物品具有一些价值参数和花费参数,要求
在满足花费限制下最大化价值或者方案数。
◦最简单几种类型以及模型
◦ 0/1背包
◦完全背包
◦多重背包
>0/1背包问题
◦给出n个物品,每个物品有Vi的价值和Wi的费用,我们总共有m块钱,求
最多能得到多少价值的物品。
◦ N<=10^3,m<=10^3
>Solution

◦设dp[i][j]表示前i个物品,用了j的体积得到的最大的价值。
◦则dp[i][j]=max{dp[i-1][j] , dp[i-1][j-w[i]]+v[i]}
◦复杂度O(N*M)
◦如果要记录方案数呢?
◦如果要求输出方案呢?
>在有价值情况下求方案数??
原来的式子是dp[i][j]=max{dp[i-1][j] , dp[i-1][j-w[i]]+v[i]} ,dp[ ][ ] 是最大价值
现在设方案数为 f[ ][ ]
如果dp[i-1][j] > dp[i-1][j-w[i]]+v[i] ,那么就会选择第一种转移过来
如果dp[i-1][j] < dp[i-1][j-w[i]]+v[i] ,那么就会选择第二种转移过来
所以 f[i][j]=max(f[i-1][j],f[i-1][j-wi]}
如果dp[i-1][j] = dp[i-1][j-w[i]]+v[i] ,那么就两种都加起来
f[i][j]=f[i-1][j]+f[i-1][j-wi]
>完全背包
◦每一个物品可以选无限个。
◦ dp[i][j]=max{dp[i][j-w[i]],dp[i-1][j]}
◦在这里提一下一个贪心的预处理
◦对于所有 Vi≥Vj, Ci≤Cj 的物品 i,都可以完全扔掉
◦对于体积相同的物品只需要留下价值最大的物品
◦对于随即数据这个优化的力度非常大。

>多重背包
◦对每一个物品,最多能用t[i]次。
◦最暴力的方法就是转移的时候枚举这个物品选几个即可。
◦ dp[i][j] = max{ dp[i-1][j-w[i]*k] + v[i]*k | k<=t[i]}
◦复杂度O( N*M*t[i] )

多重背包
◦优化一:可以把t[i]拆成1+2+4+8…2^k+x, 这样k+1组, x小于2^(k+1) ,然后
我们会发现这些组能拼成0…t[i]每一种情况,然后这样我们就成了
n*log(t[i])个物品的0/1背包问题。
◦对于[0,2^(k+1)-1]都能拼成,所以[x,2^(k+1)-1+x]也都能拼成, x<=2^(k+1)-1,
则[0,2^(k+1)-1+x]全能拼成。
◦复杂度O(n*log(t[i])*m)
多重背包另一个优化
◦我们来观察一下式子
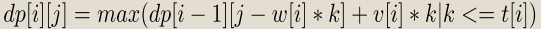
◦我们发现对于第二维,我们的j和能转移过来的j-w[i]*k在模w[i]意义下是同
余的,也就是说我们可以对于第二维按照模w[i]进行分类,不同类之间不
会互相影响。
◦设f[j]=dp[i-1][j*w[i]+r]。 r是我们枚举模w[i]的一个类。

◦实际上就是一个滑动窗口取最值的问题,直接单调队列优化即可。


◦单调队列均摊是O(m)
◦总复杂度就是O(n*m)的了。
多重背包的一个细节
◦首先我们之前都是在求最优值。单调队列和二进制分组的方法都是对的。
◦但是如果要求方案数呢?
◦这两种方法还都是对的吗?
>方案数求前缀和就不需要单调队列了
>分组背包
◦一共有n组,每组有size[i]个物品,第i组第j个物品的费用为w[i][j],价值
v[i][j],每个组里的物品是互斥的,意味着你在一组物品中只能选择一个
物品,求花费小于等于m能得到的最大价值。
◦ Size之和小于等于1000, m<=1000

经典例题
◦给出n个化学反应,每个反应消耗a[i]升氧气和b[i]升氢气,可以得到w[i]的
价值,现在总共有X升氧气和Y升氢气,求我们最多可以得到多少价值。
◦ n,a[i],b[i],X,Y<=100
>二维背包问题
◦此外还有二维背包问题,实质上和本身和普通背包毫无思维上的区别。
◦因为限制条件多了一个,所以我们需要给最初最基本的dp多加一维状态。
◦设dp[i][x][y]表示前i个物品,消耗了x的氧气和y的氢气所能得到的最大收
益是多少。
◦然后考虑一个物品选还是不选即可。
对于一般的背包问题
◦做背包问题最关键的就是找清楚并反问自己?
◦这题里面 什么是容量? 什么是物品? 什么是物品的费用? 什么是
物品的价值?
◦容量,就是这题当中我们怎样表示状态的数组。
◦费用,就是用来f[i]---->f[i+v[k]],状态转移的跨度。
◦价值,就是你这个dp的数组,所维护的东西。维护的数值!
◦背包dp一定要理解好这三点,因为很多时候题目中的“费用”并非背包
dp中的“费用”
>vijos1240
◦ 1.给你一些房间,告诉你这些房间的容纳人数和价格。
2.安排一定数量的人住到旅馆里,满足:
a.不同性别的人如果不是夫妻那么不能住一个房间。
b.一对夫妻如果住在一起,那么房间不能安排其他的人进去哪怕房间
没盛满人。
◦你来写一个程序帮助佳佳找到安排这些来参加旅行的人住进旅馆所需要
的最小花费。
◦ M:参加旅行的男性人数、 f:参加旅行的女性人数、 r:旅馆的房间数、
c:这些男女中有多少对夫妻、 Bi:每个房子容纳人数和、 Pi:每个房子
价格。注意每一个人不是单身就是和他/她唯一的妻子/丈夫一起参加旅行。
◦ 0<=m,f,r<=300, 0<=c<=Min(m,f), 0<=Pi<=10。 2<=Bi<=300
>Solution
◦还是要先明确,对于一道背包dp的题目来说,我们需要有容量,物品,
费用,价值(权值,因为有些题要求最小)。
◦本题中:求给所有的人安排房间的最小支出是多少?
那么在这里,几个人对应就是dp的数组下标
每个房间就是一个物品
房间支出就是物品的权值。
虽然这里看上去房间支出是花费,是作为数组下标的存在
实际上是作为我们要求的东西,是dp数组存的内容。
◦当然肯定不是这么简单就完了的。
>先观察一个性质
◦首先要观察出题目的一个小性质,即如果有两对(或以上)夫妻住在一起的
话,那么交换之后结果不会变差。因为首先这两个房间的容量至少为2,
如果男男在一个房间,女女在一个房间此时花费不变,有一个房间容量
大于2的时候,就还可以再入住其他人。这样结果变得更优了。 综上,要
么至多存在1对夫妻住在一起,要么不存在夫妻住在一起。
◦ f [ i,j,k,0 ]表示前 i 个房间住 j 名男性 k 名女性并且没有夫妇住在一起的最小花费
◦ f [ i,j,k,1 ]表示前 i 个房间住 j 名男性 k 名女性并且有一对夫妇住在一起的最小花费
◦ f [ i,j,k,0 ] = min( f[ i-1,j,k,0 ] , f[ i-1,j-v[i],k,0 ]+p[i] , f[ i-1,j,k-v[i],0 ]+p[i] )
◦ f[ i,j,k,1 ] = min( f[ i-1,j,k,1] , f[ i-1,j-v[i],k,1 ]+p[i] , f[ i-1,j,k-v[i],1 ]+p[i] , f[ i-1,j-1,k-1,0 ]+p[i] )
这题hin强
>1190: [HNOI2007]梦幻岛宝珠
◦给你N颗宝石,每颗宝石都有重量和价值V。要你从这些宝石中选取一些
宝石,保证总重量不超过W,且总价值最大为,并输出最大的总价值,每
颗宝石的重量符合a*2^b。
◦ V<=1e9
◦ a<=10; b<=30
>Solution
每颗宝石的重量符合a*2^b , 就是重量可以写成这个形式
二进制拆分一下
1 0 1 0 0 1 1 1 0
f[i][j]到前 i 位,剩下 j*2^i 的重量可用
◦看到w很大,看似不可做。
◦但是这题肯定能做啊!我们就找有什么特殊的约束条件。
◦ w=a*2^b,我们发现a, b都不大,就启发我们用2^b分组。
◦将物品按b值从大到小排序分阶段处理,在阶段内b值都相同,直接忽略
不足2^b的部分, f[i][j]表示前i个物品,剩余的能用重量为j*2^b的最大价
值。
◦从上一阶段到下一阶段时,将f[i][j]->f ’[i][j*2+零碎部分],注意到n=100,
a<=10,所以剩余重量最多纪录到1000即可。
◦复杂度O(n*1000)
几个背包变种和模型
>对比前两道题
◦第一道是求最优值,第二道是求方案数。
◦方案数是可以取逆的,但是最优值是无减法定义的。
◦所以第一道不能用第二道的方法也就是不能把复杂度降到O(n*m)。
◦如果第一题的Q是1000的话,可以有复杂度更优的做法吗?
>经典题
◦给出n个物品,每个物品有体积v[i],要求把物品分成两堆,然后使得两堆
物品体积的绝对值最小。
◦ n,v[i]<=100
>Solution
可行性的背包问题
◦我们设总体积为sum,那么我们必定会存在一堆体积和是小于等于sum/2
的,然后就是要求去选出一些物品总体积小于等于sum/2,最大能取到的
体积是多少。
◦这就是经典的背包问题了。
◦同时可行性的背包问题可以bitset优化
整数划分模型
一类整数划分问题
◦ 1:求把n划分成k个正整数的方案数?
◦ 2:求把n划分成互不相同k个正整数的方案数?
◦ 3:求把n划分成k个不大于m的互不相同正整数的方案数?
◦ 4:求把n划分成k个奇数的方案数?
◦ ………………………………………………
◦如果n,k和m是同阶的,我们看看最优能做到多少的复杂度。
求把n划分成k个正整数的方案数:
1.暴力dp
◦设dp[i][j][sum]前i个数,选了j个数,和为sum的方案数是多少,答案就是
dp[n][k][n],考虑这一个数选几个来转移即可。这个状态是n*k*n的转移
O(sum/i)。均摊O(n*k*n*log(n))复杂度有些高。
◦本质是个完全背包的,那种写法的话可以做到O(n*k*n)。
2.非暴力
◦我们直接设dp[i][j]表示把 i 划分成 j 个数的方案数。 ans=dp[n][k]
◦我们可以得到dp[i][j]=dp[i-j][j]+dp[i-1][j-1]。以下是dp[22][4]的两类情况:
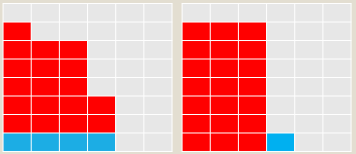
考虑有没有1的部分。
◦我们考虑数形结合来理解。
◦考虑去掉蓝色的部分。
◦左图代表: dp[ i-j ][ j ]
◦右图代表: dp[ i-1 ][ j-1 ]
满足状态转移要考虑的所有可能性!
求把n划分成互不相同k个正整数的方案数:
1.暴力
◦大同小异。
◦暴力dp:设dp[i][j][sum]前i个数,选了j个数,和为sum的方案数是多少,答
案就是dp[n][k][n],考虑下一个数选不选来转移即可。
◦本质是个0/1背包, 复杂度O(n*k*n)
2.非暴力
◦正解也是大同小异。
◦我们还是直接设dp[i][j]表示把 i 划分成 j 个数的方案数。
◦我们可以得到dp[i][j]=dp[i-j][j]+dp[i-j][j-1]。考虑去掉蓝色的部分。
◦左图代表: dp[i-j][j]
◦右图代表: dp[i-j][j-1]
◦与上一题不同这里第一维
◦是[i-j],因为要限制没有相同的数字
◦这里复杂度比上题更低!! 
求把n划分成k个不大于m的互不相同正整数的方案数。
◦背包dp的方法同上。
◦ N=20,k=4,m=6的不合法方案如图。
◦ dp[i][j] = dp[i-j][j] + dp[i-j][j-1] - dp[i-(m+1)][j-1]
◦减的这一项就是超过线的那种情况。

P4104 [HEOI2014]平衡
>BZOJ 3612(就是上面那个链接)
◦给定一个杠杆,等距均匀分布一共2n+1个等重质点,支点在n+1处,求拿
走k个质点后使杠杆仍然保持平衡的方案数 mod p的值。
◦ 1 <= n <= 10000, 1 <= k <= 10, 2 <= p <= 10000,且 k <= 2n+1
>Solution
左边距离之和=右边距离之和
◦其实就是 -n ~ n 中求选k个不同的数,和为0的方案数。
◦显然求出来f[i][j]表示选出j个数和为i的方案数,然后枚举其中一端拿走几
个a,以及拿走的数的重量之和x,把f[x][a]*f[x][k-a]累加之和就是最后的
答案了。
◦这里 j 个数是互不相同的,也就转化成了我们的“把n划分成互不相同k个
正整数的方案数”
◦算f的复杂度和统计答案的复杂度均是O(n*k*k)。
求把n划分成k个奇数的方案数?
可重复数字纯奇纯偶划分
◦ g[i][j]:将 i 划分为 j 个偶数
◦ f[i][j]:将 i 划分为 j 个奇数
g[i][j] = f[i - j][j]; f[i][j] = f[i - 1][j - 1] + g[i - j][j];
◦不可重复也是一样的。
由此类问题对状态转移的一点感触
◦ dp问题中,转移就是分情况讨论,每种情况对应一个方案数或最优值,
而这个方案数或最优值可以表示为之前已经求出来的dp值的组合。
◦只不过分情况讨论可能方法很多,以一种方式讨论能转化为已知的dp值
的叠加,另一种方式也可以。我们需要保证的是:讨论不漏掉任何情况,
像计数问题也不能出现方案重叠(求max和min其实是可以重叠的),同
时选择分类项数尽量少的方案,以便得到更优的复杂度。
◦上面几道题的转移方式可能没有原先一些问题的分类方式直观,但是也
的确满足了不重不漏尽量简洁的条件。当然这可能也并非是唯一的转移
方式,只要保证能划归到之前已经求出的dp值就行。
状态转移的一点感触
◦ 1:分类讨论要不重不漏。
◦ 2:讨论时要保证划归到的dp状态已经求出来,而不是还未求的。
◦以上保证正确性。
◦实际上能保证以上两点,无论怎样的转移方式都是可行的。
◦ 3:尽量分的类少一些,转移更快速。
◦这是关于复杂度。
总结