DP&图论 DAY 1 下午
区间和序列上的DP
序列上的DP
>序列上的dp状态设计最基本的形式
F[i]表示以 i 结尾的最优值或方案数。
◦ F[i][k]表示以 i 结尾附加信息为k的最优值或方案数。
◦当然可以有多维附加信息。
◦转移的话往往是枚举上一个断点。
◦ F[i]=max { F[j]+ w(j+1,i) | j是一个满足转移条件的断点}。
◦另一个很常见的是: f[i][j]前i个位置分成j段/选出j个的最优值。
◦这是最简单的一类序列上的dp。
>bzoj1003
◦有m个码头和e条航线,每天航线有成本。有连续n天需要从1号码头到m
号码头运输货物。每个码头会在某些天数区间内不许经过。每更换一次
运输路线,要付出k的成本。
◦求这n天的最小总成本。
◦ m<=20, n<=100
>Solution
◦其实就是分成很多段,每一段选同一个运输路线,然后得到一个最优的
划分方案,使得成本最小。
◦ f[i]表示前i天的运输最小成本。
◦ f[i]=min{ f[j]+k+w(j+1,i)*(i-j) | j<i }
◦其中w(x,y)表示最短的在第x天到第y天都能用的路线长度,把能在则几天
一直走的点加进图中,跑最短路径即可。
◦复杂度O(N^2 * m * log(m))
>bzoj1296 粉刷匠
有n条木板要被粉刷,每条木板分为m个格子,每个格子需要被刷成蓝色
或红色。
◦每次粉刷可以在一条木板上给连续的一段格子刷上相同的颜色。每个格
子最多被刷一次。
◦问若只能刷k次,最多正确粉刷多少格子。
◦ n,m<=50, k<=2500
>Solution
如果只有一条木板,那么设g[i][j]表示前i个格子刷j次的最多正确格子
◦ g[i][j]=max{ g[k][j-1]+w(k+1,i) | k<i }
◦ w(x,y)为第x到第y个格子的最多同色格子数,哪个颜色出现的多刷哪个,
直接记一个前缀和即可。
◦有多条木板,设f[i][j]表示前i个木板刷j次的最大答案。
◦ f[i][j]=Max{ f[i-1][k]+gi[m][j-k] | k<=j }
◦其实像这种一般的dp,就是把影响答案的信息用多维状态来表示,什么
必要什么就放在状态里。
括号序列模型及解法
>Codeforces314E
◦给定一个长度为n的仅包含左右括号和问号的字符串,将问号变成左括号
或右括号使得该括号序列合法,求方案总数。
◦例如(())与()()都是合法的括号序列。
◦ n<=3000。
>Solution
◦括号序列问题,往往就是把左括号看成+1,右括号看成-1,我们只需要
保证任意一个前缀大于等于0,且总和为0,就代表是个合法括号序列了。
◦令dp[i][j]表示当前到第i个字符,现在还有j个左括号。
◦那么分三种情况考虑。
◦若第i+1个字符是左括号,则能转移到dp[i+1][j+1]。
◦若第i+1个字符是右括号,则能转移到dp[i+1][j-1]。
◦若第i+1个字符是问号,则能转移到dp[i+1][j-1]与dp[i+1][j+1]。
◦最终dp[n][0]就是方案总数啦。
◦时间复杂度为O(n^2)。
>bzoj4922
给出一些括号序列,要求选择一些括号序列拼接成一个合法的括号序列,
使得总长最大。
◦ 1<=n<=300,表示括号序列的个数
◦括号序列的长度len不超过300.
>Solution
◦首先对于每个括号序列,把左边的左括号和右边的右括号对消,最后能
得到一坨这样的东西:
◦ ))…))((…((
◦就是x个右括号然后y个左括号,记作(x,y)
◦然后考虑假如我们的子集选好了,我们要按照什么顺序拼接才能拼成一
个合法的括号序列呢?
◦这就转化成了另一个问题: BZOJ3709。
◦贪心: noip的贪心很多都是按照某种方式排序,然后依次选或处理。
◦我们来看看应该怎么排序。
◦关于本题:
◦ 1:如果a[i]-d[i]>0,说明打掉这个怪兽有血可恢复,那么血量会变多,明
显我们按照伤害d[i]从小到大排序即可,然后一个个杀下来。
◦ 2:如果a[i]-d[i]<0,说明会亏血。一个精妙的想法就是,最后剩余的血量
值,假设是x,那么x是固定的。然后可以看作初始血量为x,怪兽的属性
a,d交换,这样就和上一种情况一样了。 (如图)

◦我们还是把左括号看成+1,右括号看成-1,同样是保证任意一个前缀大
于等于0,且总和为0。
◦那就是每一个给定的序列都是 先-Li再+Ri, Li是对消后左端右括号的数量,
Li是对消后右端左括号的数量。然后依次拼起来之后任何一个前缀都大于
等于0,这个其实和刚刚所讲的题目完全一样。
◦我们按照上一题的做法排序即可,排序后我们从左往右做dp。
◦设f[i][j]为 前i个括号序列-1与+1的和j个时选出括号序列最长的长度和。
◦ 也就是 前i个括号序列左括号比右括号多j个时的最长的长度和。
◦转移时考虑下一个括号序列选不选即可。
◦ Len[i]为排完序后第i个括号序列的长度。
◦ f[i+1][j-L[i+1]+R[i+1]]f[i][j] + len[i+1] (j>=L[i+1])
◦ f[i+1][j]f[i][j]
◦最后答案就是f[n][0]. 复杂度O(n*len*len)
一套有趣的题目
◦ 1: 1,2,3…n 以此进栈,求有多少种可能的出栈序列。
◦ 2:由n对括号形成的合法的括号序列由多少个。
◦ N<=10^5
◦这个问题还有很多其他的表达形式。
◦ 3:n个节点共能构成多少种二叉树,左右子树是认为不同。
◦ 4:凸多边形的三角划分的方案数:把一个凸多边形用n-3条直线连接n-3对
顶点,共形成n-2个三角形,求方案数。
◦ 5:一个n*n的格子,从(0,0)走到(n,n),求不跨过(0,0)->(n,n)这条直线的路
径方案数。
卡特兰数
◦我们设f[n]表示n个数依次进栈所能形成的出栈序列数。
◦似乎和之前不一样,好像不是划分成一段一段那样的简单形式。
◦我们可以考虑另一种形式的状态转移方式,以转移到子问题。
◦注意一段一段划分我们可以枚举最后一段的起点,但是这里不是一段一
段的,我们要考虑另外的转移方式。
◦实际上我们发现我们可以枚举1这个数是什么时候出栈的。
◦那么我们可以得到
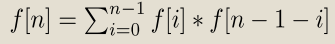
◦其实还有一个更简便的形式 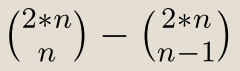
◦或 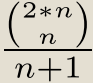
另一个经典问题
>一个经典题
◦有n个数,选择其中若干数,使得每连续k个数中都至少有一个数被选中,
且选出的数的和最小。
◦ k<=n<=1000。
◦ k<=n<=100000
>Solution
◦令dp[i]表示前i个数满足题目要求且第i个数被选中,这样的情况下选出的
数的和最少是多少。
◦通过枚举上一个被选出的数j在哪里,有dp[i]=min{dp[j]+a[i]},其中要满足
的条件为i-j<=k。
◦时间复杂度为n^2。
◦我们合法的转移区间不断向右移动,而这就是一个典型的滑动窗口问题。
单调队列优化
◦观察式子dp[i]=min{dp[j]}+a[i]。 (i-j<=k)
◦对于两个决策 j1 , j2 , 满足 j1 < j2 。
◦若dp[j1]<dp[j2],则当i-j1>k, i-j2<=k时, j2能代替j1。
◦若dp[j1]>=dp[j2],则无论何时, j1都不可能比j2优,可以直接删除。
◦每次在队列末尾插入删除一个数或者在队首删除一个数,且该队列始终
保持单调递增。
◦因此称为单调队列优化。
◦每个数进入队列出队列一次,转移是O(1)的,总时间复杂度为O(n)。
◦ q即维护的单调队列。

一种经典优化技巧
Vocabulary简化版
◦给定3个等长的只包含“?”或小写字母的字符串s,其中“?”表示可能是任意
一个小写字母。
◦已知3个字符串的字典序是升序的且互不相同。
◦问方案总数。
◦ |s|<=1000。
◦ |s|<=100000。
>Solution
◦令dp[i][0/1][0/1]表示前i个字符,第一个字符串是否等于第二个字符串,
第二字符串是否等于第三个字符串。
◦枚举第i+1位所有问号是什么字母,直接转移。
◦复杂度O(n*26^3)。
◦如何优化?
◦预处理转移的系数,是个很经典的优化技巧。
◦预处理出f[i][j][k][0/1][0/1][0/1][0/1]表示下一个位置,第一个串字符是i,
第二个串字符是j,第三个串字符是k,由于可能出现”?”的情况,我们用0
表示”?”。前两个[0/1]表示之前的位置1和2串是否相等, 2和3串是否相等,
后两个[0/1]表示将下一个位置所有”?”用字母代替后,第1个串的与第二个
串的是否相等, 2和3串是否相等,在转移时直接拿f数组转移。
◦利用这个转移系数的数组做dp的时间复杂度就是O(n)的了。
◦预处理就直接,枚举问号怎么选,即可,复杂度O(27^3*2^2…..)。