P1040 加分二叉树
加分二叉树或许是你在考场上做完这道题就会加分的一棵神奇的树,就像AC自动机一样amazing
前置知识
1.前序遍历: 根结点在最前 即 头 左 右
2.中序遍历:根结点在中间 即 左 右 头
3.后序遍历:根结点在最后 即 左 右 头
理解一下题意(在这里栽了个大坑)
题目给出一个树的中序遍历,要在这个中序遍历的条件限制下,得到最大加分,并且输出此时的加分二叉树的前序遍历
一定要在给出的中序遍历的条件限制下,一定一定一定
所以解答有两步
1.求最大加分
我们可以把问题小化,也就是先求由1个数字构成加分树的最大加分,再求2个的,一直求到n个的,最大加分累加(也不算是累加)最后得到最优解
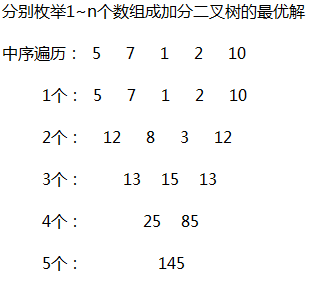
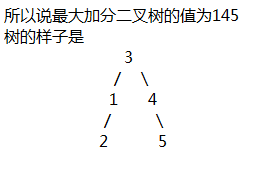
以下是错误解答

2.求前序遍历
可以递归求解
先输出根结点
然后递归左子树
然后递归右子树
代码
1.记忆化搜索(由于这道题数据很水,所以可以擦边过,样例大了估计要WA)
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<cstdlib> using namespace std; int n,gen[31][31]; long long ans; int a[31],dis[31][31]; int dfs(int l,int r) //记忆化搜索 { if(dis[l][r]>0) return dis[l][r]; //已经计算过加分了,直接返回 if(l==r) return a[l]; //单元素区间根为自己 if(r<l) return 1; //空子树 for(int i=l;i<=r;i++) //寻找在区间[l,r]内以那个点为根加分最大 { int p=dfs(l,i-1)*dfs(i+1,r)+a[i]; if(dis[l][r]<p) { dis[l][r]=p; gen[l][r]=i; } } return dis[l][r]; //得到最大加分 } void qianxu (int l,int r) //前序遍历:头 左 右 { if(r<l) return; //这个区间不合法 if(l==r) {printf("%d ",l); return;} //该区间只有一个数 printf("%d ",gen[l][r]); //头 qianxu(l,gen[l][r]-1); //左 qianxu(gen[l][r]+1,r); //右 } int main() { int n; scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); dis[i][i]=a[i]; //初始化,单元素区间加分为自己的加分 gen[i][i]=i; //单元素区间的根为自己 } ans= dfs(1,n); //区间[1,n]的加分 printf("%ld ",ans); qianxu(1,n); //递归出结果 return 0; }
2.区间DP
注意此处是在开区间的大前提下进行
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<string> #include<cstring> #include<cstdlib> using namespace std; int n,a[35],gen[35][35]; int dp[35][35]; // dp[l][r],gen[l][r] ->ans in [l,r) int dfs(int l,int r) { printf("%d ",gen[l][r]); //头 if(gen[l][r]>l) //左 dfs(l,gen[l][r]); if(gen[l][r]+1<r) //右 dfs(gen[l][r]+1,r); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&dp[i][i+1]); gen[i][i+1]=i; dp[i][i]=1; //空子树 } for(int l=2;l<=n;l++) //枚举区间长度 for(int i=1;i<=n-l+1;i++) //区间起点 { int j=i+l; //区间终点 for(int k=i;k<j;k++) //枚举根结点 { if(dp[i][j]<dp[i][k]*dp[k+1][j]+dp[k][k+1]) //更新最大加分 { dp[i][j]=dp[i][k]*dp[k+1][j]+dp[k][k+1]; gen[i][j]=k; } } } printf("%d ",dp[1][n+1]); dfs(1,n+1); //开区间递归出答案 return 0; }
感悟
1.不要手误打错输出格式,哪里加&,哪里不加&,输出的时候加了那就会输出存储空间
2.检查一下for循环的条件OK???