高精度计算
看一下c++存储范围:
Int &long long范围:
Int [ -231 , 231-1 ]
long long [ -263 , 263-1 ] ≈ 1020
由于C++储存的最大整数是 long long 类型的,2^63左右,可是如果我们要计算的数超过了这个范围,那就会爆了,是时候引入高精度计算了。
高精度计算要把需要运算的数转化为字符串读入,否则会炸
高精度计算方法:竖式加减乘除法
用数组存储数字每一位
比如,一个数组z
把19260817存进数组z
倒序存,保证个位对齐
所以下标为 i,表示这个数的10i 位

我们希望可以写一个高精度的板子,int 可以实现的,gaojing 也可以实现
高精度加法
思路:模拟竖式计算
注意:(1)进位
(2)倒序计算


1.整体框架
一般 int 类型的加法
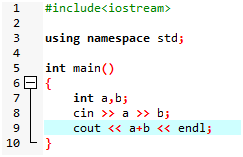
粘进来高精度板子
希望写一个高精度模板
Int 实现,改成gaojing

2.结构体

3.初始化
不同编译器对于这两个东西初始值不同,所以要初始化

ps:析构函数:防止内存泄漏 此处用不到
4.重载cin cout (放在gaojing里面)
友元函数 friend Istream 读入流 & 取址
用cin 把a读到高精度里
static静态变量 不可去掉
一般不可以在函数里开数组的局部变量
要用static,否则爆栈
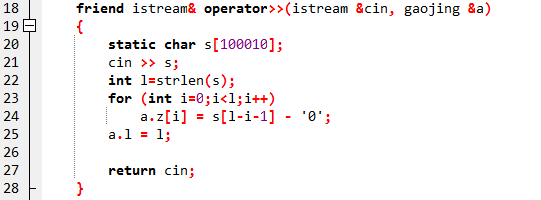
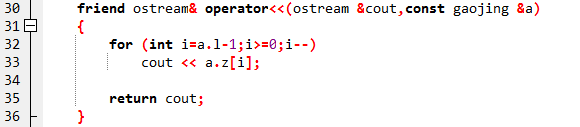
Const 保证不会改变a
从高位到低位输出
有原函数必须放在类里面声明
5.重载运算符:

我们重载运算符,希望板子可以直接实现以上操作
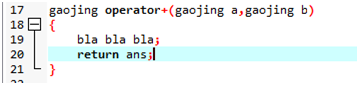
定义高精度的a和高精度的b加法运算,返回类型也是高精度的值
不会影响int的加法运算
BUT!!!!
 写法有问题
写法有问题
~~~没有看出问题,没有打好基础QAQ~~~
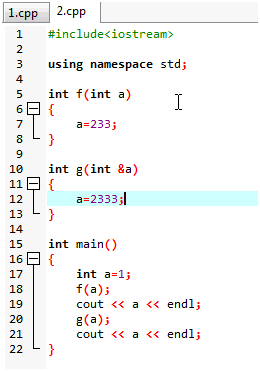
输出1,2333
加了取址符号&,就是直接引用a的值,更改的话更改a的值
不加取址符号&,就是拷贝一份a的备份a’,更改的话更改a’的值
So,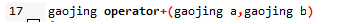
每次调用会拷贝一份二十万位的数组,很慢
改成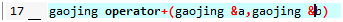
还是有问题
操作过程中可能会改变a的值
为了避免手抖改数字,加上const,同时为了更好的引用STL
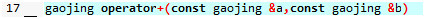

看代码:(ZHX版本)
#include<iostream> #include<cstdlib> #include<cstring> using namespace std; struct gaojing { int z[100010]; int l; gaojing() { l=1; memset(z,0,sizeof(z)); } friend istream& operator>>(istream &cin, gaojing &a) { static char s[100010]; cin >> s; int l=strlen(s); for (int i=0;i<l;i++) a.z[i] = s[l-i-1] - '0'; a.l = l; return cin; } friend ostream& operator<<(ostream &cout,const gaojing &a) { for (int i=a.l-1;i>=0;i--) cout << a.z[i]; return cout; } }; gaojing operator+(const gaojing &a,const gaojing &b) { gaojing c; int l = max(a.l,b.l); for (int i=0;i<l;i++) { c.z[i] += a.z[i] + b.z[i]; c.z[i+1] += c.z[i] / 10; c.z[i] = c.z[i] % 10; } if (c.z[l] != 0) l++; c.l = l; return c; } int main() { gaojing a,b; cin >> a >> b; a+b; cout << a+b << endl; }
(白书版本)
#include<iostream> #include<algorithm> #include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> using namespace std; char a1[10000],b1[10000]; int a[10000],b[10000],c[10000]; int main() { scanf("%s",a1); scanf("%s",b1);
int lena=strlen(a1); int lenb=strlen(b1);
for(int i=lena-1;i>=0;i--) a[lena-i]=a1[i]-'0'; //字符串转数字 for(int i=lenb-1;i>=0;i--) b[lenb-i]=b1[i]-'0';
int len=max(lena,lenb);
for(int i=1;i<=len;i++) c[i]=a[i]+b[i]; for(int i=1;i<=len;i++) { c[i+1]+=c[i]/10; //处理进位 c[i]%=10; }
if(c[len+1]>0) len++; //处理最高位
for(int i=len;i>0;i--) printf("%d",c[i]);
return 0; }
高精度减法
思路:模拟竖式计算,进位变退位
注意:(1)大减小为负数
(2)借位减1
(3)strcmp(a1,b1),如果a1>b1,返回正数;a1=b1,返回0;a1<b1,返回负数
#include<iostream> #include<algorithm> #include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> using namespace std; char a1[10000],b1[10000],c1[10000]; int a[10000],b[10000],c[10000]; int main() { scanf("%s",a1); scanf("%s",b1); if(strlen(a1)<strlen(b1)||strlen(a1)==strlen(b1)&&strcmp(a1,b1)<0) { strcpy(c1,a1); //把a1数组的值完全赋给c1 strcpy(a1,b1); strcpy(b1,c1); cout<<"-"; } int lena=strlen(a1); int lenb=strlen(b1); for(int i=lena-1;i>=0;i--) a[lena-i]=a1[i]-'0'; for(int i=lenb-1;i>=0;i--) b[lenb-i]=b1[i]-'0'; int len=max(lena,lenb); for(int i=1;i<=len;i++) { if(a[i]<b[i]) { a[i]+=10; //借位 a[i+1]--; } c[i]=a[i]-b[i]; } if(c[len]==0&&len>0) len--; //处理前导0 for(int i=len;i>0;i--) printf("%d",c[i]); return 0; }
高精度乘法
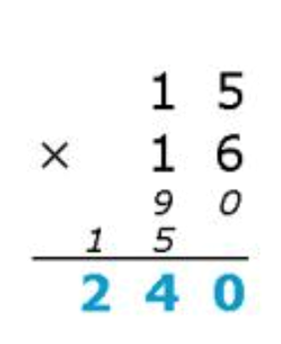
思路:模拟乘法竖式
注意:(1)判断结果正负0
(2)注意借位
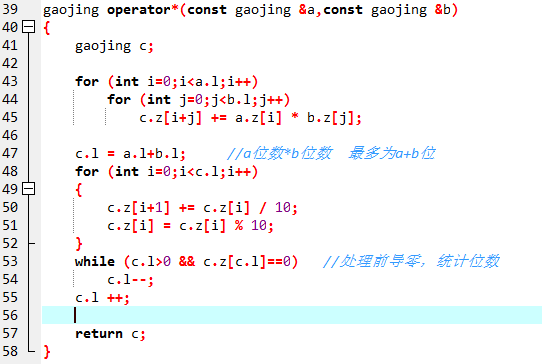
[代码]
#include<iostream> #include<cstdlib> #include<cstring> using namespace std; struct gaojing { int z[100010]; int l; gaojing() { l=1; memset(z,0,sizeof(z)); } friend istream& operator>>(istream &cin, gaojing &a) { static char s[100010]; cin >> s; int l=strlen(s); for (int i=0;i<l;i++) a.z[i] = s[l-i-1] - '0'; a.l = l; return cin; } friend ostream& operator<<(ostream &cout,const gaojing &a) { for (int i=a.l-1;i>=0;i--) cout << a.z[i]; return cout; } }; gaojing operator*(const gaojing &a,const gaojing &b) { gaojing c; for (int i=0;i<a.l;i++) for (int j=0;j<b.l;j++) c.z[i+j] += a.z[i] * b.z[j]; c.l = a.l+b.l; for (int i=0;i<c.l;i++) { c.z[i+1] += c.z[i] / 10; c.z[i] = c.z[i] % 10; } while (c.l>0 && c.z[c.l]==0) c.l--; c.l ++; return c; } int main() { gaojing a,b; cin >> a >> b; cout << a*b << endl; }
白书代码:
#include<iostream> #include<cstdio> #include<cmath> #include<string> #include<cstring> #include<algorithm> using namespace std; char a1[200001],b1[200001]; int a[200001],b[200001],c[5000000],lena,lenb,lenc,x,i,j; int main() { scanf("%s",a1); scanf("%s",b1); if(a1[0]=='0'||b1[0]=='0') { cout<<"0"; return 0; } lena=strlen(a1); lenb=strlen(b1); if(a1[0]=='-'&&b[0]!='-') { cout<<"-"; for(i=0;i<=lena-1;i++) a1[i]=a1[i+1]; lena--; } if(a1[0]!='-'&&b[0]=='-') { cout<<"-"; for(i=0;i<=lenb-1;i++) b1[i]=b1[i+1]; lenb--; } if(a1[0]=='-'&&b[0]=='-') { for(i=0;i<=lena-1;i++) a1[i]=a1[i+1]; lena--; for(i=0;i<=lenb-1;i++) b1[i]=b1[i+1]; lenb--; } for(i=0;i<=lena-1;i++) a[lena-i]=a1[i]-'0'; for(i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-'0'; for(i=1;i<=lena;i++) { x=0; for(j=1;j<=lenb;j++) { c[i+j-1]=a[i]*b[j]+x+c[i+j-1]; x=c[i+j-1]/10; c[i+j-1]%=10; } c[i+lenb]=x; } lenc=lena+lenb; while(c[lenc]==0&&lenc>0) lenc--; for(i=lenc;i>=1;i--) cout<<c[i]; cout<<endl; return 0; }
高精度除法(常用高精度除以低精度)
1.高精度除以低精度(lyd版本)
void div(gaojing a,int b) { int t=0; for(int i=a.size-1;i>=0;i--) { t=t*10+a.a[i]; a.a[i]=t/b; t=t%b; } while(a.a[a.size-1]==0&&a.size>1) a.size--; }
2.高精除以高精
a是被除数,b是除数
//高精度除以高精度 gaojing operator / (gaojing a,gaojing b) { gaojing c; c.size=a.size-b.size+1; for(int i=a.size-1;i>=b.size-1;i--) { a.a[i]+=a.a[i+1]*10; a.a[i+1]=0; if(a.a[i]==0) continue; for(;;) { bool geq=true; for(int j=i,k=b.size-1;k>=0;j--,k--) { if(a.a[j]>b.a[k]) {geq=true;break;} if(a.a[j]<b.a[k]) {geq=false;break;} } if(geq==false) break; c.a[i-b.size+1]++; for(int j=i-b.size+1,k=0;k<b.size;j++,k++) { if(a.a[j]<b.a[k]) { a.a[j+1]--; a.a[j]+=10; } a.a[j]-=b.a[k]; } } } for(;!c.a[size-1]&&c.size>1;c.size--) return c; }
思路:模拟除法式子
#include<iostream> #include<algorithm> #include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> using namespace std; char str[50010]; int a[50010],c[50000000]; int main() { scanf("%s", str); int len=strlen(str); for(int i=len-1;i>=0;i--) a[len-i]=str[i]-'0'; int n=len; int B; cin>>B; for(int i=n;i>0;i--) { c[i]=a[i]/B; a[i-1]+=(a[i]%B)*10; } while(c[n]==0 && n>0) n--; for(int i=n;i>0;i--) printf("%d",c[i]); return 0; }
高精度开方

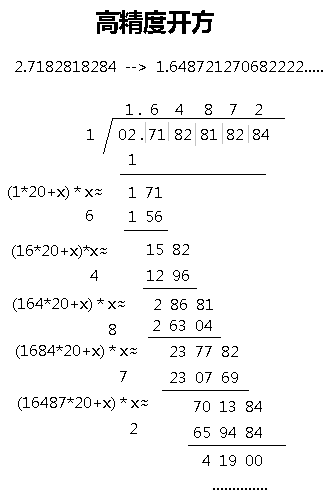
计算流程:
(1)从小数点开始,向左,2位划分一节,向右,两位划分一节,首位不够一节补0
(2)从左到右数第一节开始开方
(3)第一节开2,上位1余1,移下来第二节,得到171,当前所得答案1
考虑满足(1*20+x)* x <= 171 的最大 x 为多少,x 上位到第二节上面,此时上位 6
所得(1*20+6)* 6 =156,与原来171作差,得15,移下来第三节,得到1582
当前所得答案16
考虑满足(16*20+x)* x <= 1582 的最大 x 为多少,x 上位到第三节上面,此时上位4
所得(16*20+4)* 4 =1296,与原来1582作差,得286
< 推广 >
移下来第 i 节,得到 res ,当前所得答案 ans
考虑满足 (ans*20+x) * x<=res 的最大 x 为多少,x 上位到第 i 节上面
所得(ans*20+x)*x 与原来 res 作差,得 cha
移下来第 i+1 节,得到新的 res ,更新当前所得答案 ans
(QWQ 一不小心暴露了人类的本质 QWQ)
(4)答案不用补0,也就是一节对应答案的一位数字,得到答案别忘加小数点(如果需要的话)
PS:至于为什么乘以20啊,规定QWQ
下面简单证明一下:
比如你开方一个整数(361),得到一个两位数(19)
我们把这个两位数整数看做 x y
那么它的十进制数表示就是 (10x+y),被开方数就是(10x+y)2
( 10 x + y )2
=100 x2 + y2 +20xy
=100 x2 + y ( 20x + y )
也就相当于你先开出来一个 x ,然后再去找 y 啊,看上面的式子hin像计算流程
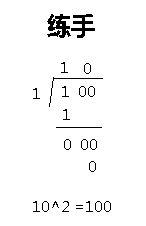
原理不想讲,自己去百度(逃)
原理是: (a*10+b)^2=100*a^2+2*a*10*b+b^2=100*a^2+(20*a+b)*b 竖式算开平方步骤:(如:把625开方) (1)先把被开方的数由右到左每二位一组。(6,25) (2)由左到右取每一组。(取的是6) (3)取某数的平方,要比第一组数小,但某数+1的平方,要比第一组数大,这就是第一个开方值。(某数是2) (4)把第一组数减去第一个开方值的平方,再取第二组数,构成余数。(6-2*2=2,余数为225) (5)把第一个开方值*20,再加上估计的第二个开方值,它与第二个开方值相乘要比余数小,但把第一个开方值*20,再加上估计的第二个开方值+1,它与第二个开方值+1相乘要比余数大。(第二个开方值取5,2*20+5=45,45*5=225) 所以(625)^0.5=25 现在中考高考都不让带计算器了,试卷上出现的一些常见开方的数字都是直接提供给学生的。现在手工列竖式开方基本不再需要了,但是每每想起当时老师教过的列式开平方的方法,还是很骄傲的。 手工开平方的原理实际是很简单的,原理如下 (a+b)^2=a^2+2ab+b^2=a^2+(2a+b)*b 这里的a取10的倍数,b取个位数,如(10+2)^2=10^2+(2*10+2)*2=100+22*2=144,这是知道结果时的推算,如何给你一个数字,让你推算它的开平方值呢? 现在要对144开平方,那么估计所求的值为十几,因此可以写成(10+?)^2=10^2+(2*10+?)*?,这样猜这个?为2时,再代入计算,发现计算出的值正确。按此方法,可以列竖式进行计算。如果需要对2025进行开方处理,那么按两位两位进位,需要先对20求根,取5时,5*5>20,因此只能取4,也就是结果是四十几,即(40+?)^2=40^2+(2*40+?)*?,即减去40的平方1600后,2025还余下425,425再去除于8?(八十几),才能得到?(几),结论当然是85*5=425,因此2025开平方就是45。
歪门邪道
口算两位数乘法
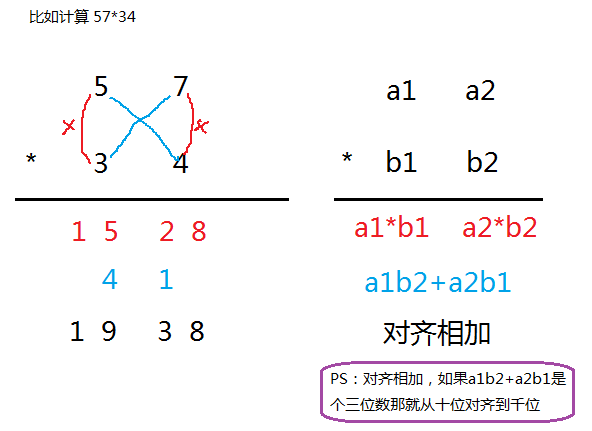
优化
举个栗子
在高精度加法
1 2 3 4 5 6 7 8 +
1 2 3 4 5 6 7 8 时
我们可以把1234存在一个数组格子里,最后就是%1000或者/1000了,只需要计算两次加法,提高效率,其他运算同理可以优化
突然我们发现一个神奇的东西,它叫做Python 3,但是考试不能用鸭
P1932 A+B A-B A*B A/B A%B Problem
a,b=int(input()),int(input()) print (a+b) print (a-b) print (a*b) print (a//b) print (a%b)