https://blog.csdn.net/ice110956/article/details/17557795
一、无约束 求偏导等于0
二、等式约束拉格朗日函数求偏导等于0
(1)
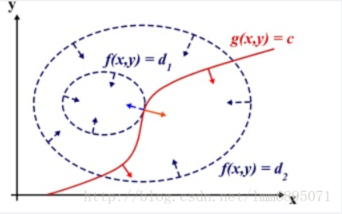
这个图是二维情况下的经典图。表明求得最优解的条件就是拉格朗日的倒数为0
(2)

以上两种情况说明了等式约束下的最优条件 (必要条件)
二阶条件hessian正定是充分条件(一维函数比如x2)
三、不等式约束满足kkt条件
四、增广拉格朗日 :增加penalty 使得更加mild condition
五、利用罚函数思想:根据约束条件构造惩罚函数加入目标函数中变为无约束问题。简言之约束问题通过惩罚变成无约束问题
Rho 是惩罚因子 Rho范数方是惩罚项,目标函数就是罚函数
可行解 惩罚项为0
不可行解 惩罚项很大。
罚函数:
外罚函数
内罚函数 就是障碍函数(内点法的障碍函数)
https://blog.csdn.net/newthinker_wei/article/details/52857397
当初学0空间补空间现在又忘了。看这篇文章看看能记起多少来
等式约束要求deltaf(x)在所有等式条件的补空间内。这样与(二)叙述的就对应起来了。博主把空间的知识和拉格朗日结合了起来会加深理解。