Java数据结构与算法(5):AVL树

AVL树是带有平衡条件的二叉查找树，它是每个节点的左子树和右子树的高度最多差1的二叉查找树。AVL树的节点定义如下：

class AVLNode<T> {
        T element;              // 键值
        int height;         // 高度
        AVLNode<T> left;
        AVLNode<T> right;
		AVLNode(T element) {
			this(element, null, null);
		}
        AVLNode(T element, AVLNode<T> left, AVLNode<T> right) {
            this.element = element;
            this.height = 0;
            this.left = left;
            this.right = right;
        }
}

根据AVL树的性质，当插入新的节点时，可能破坏平衡性质，因此需要对树进行旋转来满足平衡条件。AVL树的不平衡可以总结为4种情形：LL、RR、LR、RL，由于对称性,逻辑上可以认为两种。

单旋转

LL型

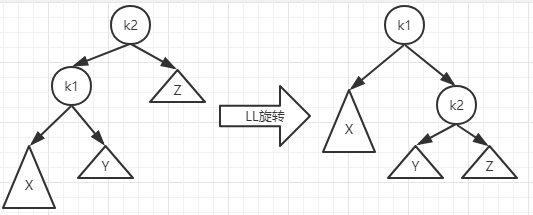
如图，当子树X插入新节点后，节点k2不满足AVL的平衡条件。为了使树恢复平衡，我们可以抽象地将树看成是柔和的，抓住k1节点使劲摇动它，在重力的作用下k1变成了新的根，k2变成了k1的右儿子，X和Z分别是k1的左儿子和k2的右儿子。子树Y介于k1和k2之间的那些节点，可以将它作为k2的左儿子，这样一棵新的AVL树诞生了。k1的高度取决于k1左子树X的高度和k1右子树k2的高度，k2的高度取决于k2的左子树Y和k2的右子树Z的高度。

LL旋转方法：

private AVLNode<T> leftLeftRotation(AVLNode<T> k2) {
        AVLNode<T> k1 = k2.left;
        k2.left = k1.right;
        k1.right = k2;
        k2.height = max(height(k2.left), height(k2.right)) + 1;
        k1.height = max(height(k1.left), k2.height) + 1;
        return k1;
    }

RR型

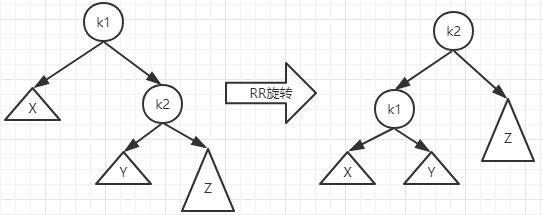
理解了上面的LL型旋转就不难理解RR型的旋转了，根据对称性，RR型也只需要通过一次单旋转就可以完成。

private AVLNode<T> rightRightRotation(AVLNode<T> k1) {
        AVLNode<T> k2 = k1.right;
        k1.right = k2.left;
        k2.left = k1;
        k1.height = max(height(k1.left), height(k1.right)) + 1;
        k2.height = max(height(k2.right), k1.height) + 1;

        return k2;
}

双旋转

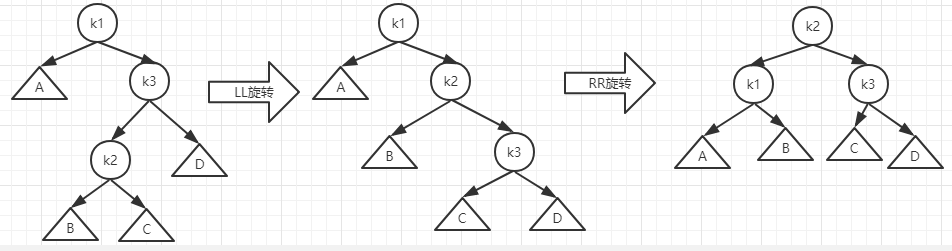
LR型

对于上图第一棵树描述的情形，由于以k2为父节点的子树为太深，这时候如果以k1为根节点，经过一次旋转后它就变成了RL型，依然不符合AVL树的平衡条件，因此，我们先忽略掉k3和D，左子树是一棵以k1为根节点的RR型二叉树，首先进行一次RR旋转，接着这就是一棵LL型树了，再次进行一次LL旋转，AVL树就生成了。

LR型旋转方式：

private AVLNode<T> leftRightRotation(AVLNode<T> k3) {
    k3.left = rightRightRotation(k3.left);
    return leftLeftRotation(k3);
}

RL型

根据对称性，理解RL型旋转应该不是一件很难的事了。RL型旋转方式：

private AVLNode<T> rightLeftRotation(AVLNode<T> k1) {
    k1.right = leftLeftRotation(k1.right);
    return rightRightRotation(k1);
}

插入

向一棵AVL树中插入新的节点时，我们的做法与二叉树查找树的思想是一样的，不同的是AVL树在插入新的节点后需要再执行一次平衡操作，如果树高度不平衡，需要进行单旋转或双旋转。

private AVLNode<T> insert(T x, AVLNode<T> t) {
    if (t == null) {
    	return new AVLNode<>(x, null, null);
    }
    int cmp = x.compareTo(t.element);
    if (cmp < 0) {
    	t.left = insert(x, t.left);
    } else if (cmp > 0) {
    	t.right = insert(x, t.right);
    } else {
    	// 重复值不处理
    }
    return balance(t);
}

balance方法：

private static final int ALLOWED_IMBALANCE = 1;
private AVLNode<T> balance(AVLNode<T> t) {
    if (t == null) {
    	return t;
    }
    // 左儿子的高度大于右儿子的高度
    if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
        if (height(t.left.left) >= height(t.left.right)) {
            // LL型-左儿子的左儿子高度大于左儿子的右儿子高度
            t = leftLeftRotation(t);
        } else {
            // LR型-左儿子的右儿子高度大于左儿子的左儿子高度
            t = leftRightRotation(t);
        }
     } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE) { 
        // 右儿子高度大于左儿子高度
        if (height(t.right.right) >= height(t.right.left)) {
            // RR型-右儿子的右儿子高度大于右儿子的左儿子高度
            t = rightRightRotation(t);
        } else {
            // RL型-右儿子的左儿子高度大于右儿子的右儿子高度
            t = rightLeftRotation(t);
        }
    }
    t.height = Math.max(height(t.left), height(t.right)) + 1;
    return t;
}

删除

理解了插入操作，我们不难了解删除操作，就是在二叉查找树的删除基础上，在最后添加平衡操作。

private AVLNode<T> remove(T x, AVLNode<T> t) {
    if (t == null) {
    	return t;
    }
    int cmp = x.compareTo(t.element);
    if (cmp < 0) {
    	t.left = remove(x, t.left);
    } else if (cmp > 0) {
    	t.right = remove(x, t.right);
    } else if (t.left != null && t.right != null) {
   		t.element = findMin(t.right).element;
    	t.right = remove(t.element, t.right);
    } else {
    	t = (t.left != null) ? t.left : t.right;
    }
    return balance(t);
}

AVL树的完成编码：

class AVLTree<T extends Comparable<T>> {
    private AVLNode<T> root;

    private int height(AVLNode<T> tree) {
        if (tree != null) {
            return tree.height;
        }
        return 0;
    }

    public int height() {
        return root.height;
    }

    public AVLNode<T> search(T element) {
        return search(root, element);
    }

    private AVLNode<T> search(AVLNode<T> x, T element) {
        if (x == null) {
            return x;
        }
        int cmp = element.compareTo(x.element);
        if (cmp < 0) {
            return search(x.left, element);
        } else if (cmp > 0) {
            return search(x.right, element);
        } else {
            return x;
        }
    }


    public AVLNode<T> insert(T x) {
        return insert(x, root);
    }

    private AVLNode<T> insert(T x, AVLNode<T> t) {
        if (t == null) {
            return new AVLNode<>(x, null, null);
        }
        int cmp = x.compareTo(t.element);
        if (cmp < 0) {
            t.left = insert(x, t.left);
        } else if (cmp > 0) {
            t.right = insert(x, t.right);
        } else {
            // 重复值不处理
        }
        return balance(t);
    }

    public AVLNode<T> remove(T x) {
        return remove(x, root);
    }

    private AVLNode<T> remove(T x, AVLNode<T> t) {
        if (t == null) {
            return t;
        }
        int cmp = x.compareTo(t.element);
        if (cmp < 0) {
            t.left = remove(x, t.left);
        } else if (cmp > 0) {
            t.right = remove(x, t.right);
        } else if (t.left != null && t.right != null) {
            t.element = findMin(t.right).element;
            t.right = remove(t.element, t.right);
        } else {
            t = (t.left != null) ? t.left : t.right;
        }
        return balance(t);
    }

    public AVLNode<T> findMax() {
        return findMax(root);
    }

    private AVLNode<T> findMax(AVLNode<T> x) {
        if (x == null) {
            return x;
        }
        while (x.right != null) {
            x = x.right;
        }
        return x;
    }

    public AVLNode<T> findMin() {
        return findMin(root);
    }

    private AVLNode<T> findMin(AVLNode<T> x) {
        if (x == null) {
            return x;
        }
        while (x.left != null) {
            x = x.left;
        }
        return x;
    }

    private AVLNode<T> leftLeftRotation(AVLNode<T> k2) {
        AVLNode<T> k1 = k2.left;
        k2.left = k1.right;
        k1.right = k2;
        k2.height = max(height(k2.left), height(k2.right)) + 1;
        k1.height = max(height(k1.left), k2.height) + 1;
        return k1;
    }

    private AVLNode<T> rightRightRotation(AVLNode<T> k1) {
        AVLNode<T> k2 = k1.right;
        k1.right = k2.left;
        k2.left = k1;
        k1.height = max(height(k1.left), height(k1.right)) + 1;
        k2.height = max(height(k2.right), k1.height) + 1;

        return k2;
    }

    private AVLNode<T> leftRightRotation(AVLNode<T> k3) {
        k3.left = rightRightRotation(k3.left);
        return leftLeftRotation(k3);
    }

    private AVLNode<T> rightLeftRotation(AVLNode<T> k1) {
        k1.right = leftLeftRotation(k1.right);
        return rightRightRotation(k1);
    }

    private int max(int a, int b) {
        return a > b ? a : b;
    }

    private static final int ALLOWED_IMBALANCE = 1;

    private AVLNode<T> balance(AVLNode<T> t) {
        if (t == null) {
            return t;
        }
        if (height(t.left) - height(t.right) > ALLOWED_IMBALANCE) {
            if (height(t.left.left) >= height(t.left.right)) {
                // LL型
                t = leftLeftRotation(t);
            } else {
                // LR型
                t = leftRightRotation(t);
            }
        } else if (height(t.right) - height(t.left) > ALLOWED_IMBALANCE) {
            if (height(t.right.right) >= height(t.right.left)) {
                // RR型
                t = rightRightRotation(t);
            } else {
                // RL型
                t = rightLeftRotation(t);
            }
        }
        t.height = Math.max(height(t.left), height(t.right)) + 1;
        return t;
    }

    private static class AVLNode<T> {
        T element;              // 键值
        int height;         // 高度
        AVLNode<T> left;
        AVLNode<T> right;

        public AVLNode(T element, AVLNode<T> left, AVLNode<T> right) {
            this.element = element;
            this.height = 0;
            this.left = left;
            this.right = right;
        }
    }
}