题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6035
题意:一棵树有n个点,每个点有自己的颜色,任意两个不同的点可以组成一条路径。也就是说一共有n(n-1)/2条不同的路径,每条路径的价值等于这条路径上颜色的数量,求所有路径的总价值。
思路:这道题采用补集的思想,我们假设总共有m个颜色出现,一共有n(n-1)/2条路径,我们假设每条路径都有m种颜色出现总价值就是m*n(n-1)/2。那么我们只要减去每种颜色在哪些路径中没有出现过,就可以得到答案。
具体做法:我们都下过围棋吧!我们把一棵树的点看成一个棋盘上棋子,被同颜色的棋子围在其中的点,和外面的点的所形成的路径都是要经过这种颜色的。而内部的点两两之间所形成的路径是不存在这种颜色,是我们需要减去的。
那么我们怎么得到这个被围在中间的点的数量呢?
题解中提到一个虚树思想。其实就是维护一个dfs过程中的值(用数组构造),在这里我们维护一个某一个颜色的dfs完返回到这个点的时候这个点下方与这个点颜色相同的点为根的子树大小。
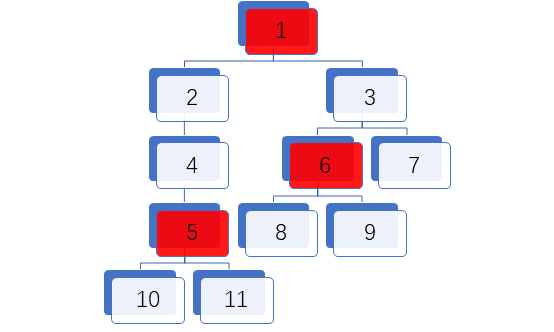
我们现在开始模拟程序的过程。
对于1节点,5节点和6节点与它颜色相同,5节点为根的子树大小为3,6节点为根的子树大小也为3,那么实际上被围在中间的点就是1节点两个后续后续节点为根的子树大小(分别是2节点和3节点),我们把2节点为根的树的大小减去5节点为根数的大小得到2就是被1节点和5节点围在中间的点的个数。3节点为根的树的大小减去6节点为根的树的大小得到被1和6节点围在中间的点的个数。那么我们怎么得到5为根的点的个数和6为根点的个数呢?
我们dfs(左边先dfs)从1开始我们一路一下当前红色节点为根的子树大小为0,我们记录一个这个值s1,然后一路dfs到底然后返回,假设我们dfs返回到5的时候,我们已经知道5的大小是3,从而我们把sum[red]更新为3。然后返回到1,我们知道对1节点的2这个子树中红色颜色为根的最大子树大小为3(通过3-0),而2这个子树的带下为5,说明有两个点不是被围在中间。这个时候我们记录一个完成2子树这个支路我们已经把红色为根子树大小已经从0更新为3,把s1更新为3。
然后我们进入1的右子树3,一路dfs到底返回到6,假设我们知道6的带下是3,那么我们应该把sum[red]+=3=6,然后返回到1的时候我们发现sum[red]-s1=3,说明3这个支路下面有有一颗大小为3颜色是红色子树6。那么被围在中间的点就是3为根树的大小减去6为根子树的大小得到被围在中间的点为5-3=2
最后1也是一颗别人的子树,我们在返回的时候需要合并1这个节点下面所有红色节点为根的子树的和即5的大小3和6的大小3,加起来等于6,而1这个树本身的大小是11,所以对于整个sum[red]的增加量就是1为根的树的大小-6等于5,完了以后sum[red]=5+6=11等于1节点为根树的大小,再返回给1的祖先,同理我们从5和6节点那里得到他返回子树的大小也是通过同样类型的方式。这个可能就是所谓的虚树的应用吧!
代码:
1 //Author: xiaowuga 2 #include <iostream> 3 #include <algorithm> 4 #include <set> 5 #include <vector> 6 #include <queue> 7 #include <cmath> 8 #include <cstring> 9 #include <cstdio> 10 #include <ctime> 11 #include <map> 12 #include <bitset> 13 #include <cctype> 14 #define maxx INT_MAX 15 #define minn INT_MIN 16 #define inf 0x3f3f3f3f 17 #define mem(s,ch) memset(s,ch,sizeof(s)) 18 #define da cout<<da<<endl 19 #define uoutput(a,i,l,r) for(int i=l;i<r;i++) if(i==l) cout<<a[i];else cout<<" "<<a[i];cout<<endl; 20 #define doutput(a,i,l,r) for(int i=r-1;i>=0;i--) if(i==r-1) cout<<a[i];else cout<<" "<<a[i];cout<<endl; 21 const long long N=200000+10; 22 using namespace std; 23 typedef long long LL; 24 LL sum[N],sz[N],col[N],vis[N]; 25 //sz[i]代表以i节点为根的子树大小 26 //col[i]代表的是i节点的颜色 27 //我们通过vis数组判断是否出现过某种颜色,以便统计出现了多少种颜色 28 //sum数组有点难理解,sum[i]表示当前i颜色的子树大小之和(在深搜过程中会值会改变。) 29 vector<int>p[N]; 30 LL cut=0,n; 31 void init(){//初始化 32 for(int i=1;i<=n;i++){ 33 p[i].clear(); 34 sum[i]=sz[i]=cut=vis[i]=0; 35 } 36 } 37 void dfs(int u,int pre){ 38 sz[u]=1; 39 LL s=sum[col[u]]; 40 LL step=0; 41 for(int i=0;i<p[u].size();i++){ 42 LL v=p[u][i]; 43 if(v==pre) continue; 44 LL s=sum[col[u]];//这个点进栈前该点颜色的树的大小 45 dfs(v,u); 46 sz[u]+=sz[v];//加上所有子树的大小计算以u点为根的树的大小 47 LL qr=sum[col[u]]-s;//qr代表这个子树下面的同颜色孙树的大小 48 step+=qr;//合并所有子树中同样颜色的孙树大小 49 LL szv=sz[v]-qr;//这个子树与同u点颜色相同的孙树之间点的数量 50 cut=cut+szv*(szv-1)/2;//计算不存在颜色u的路径数 51 } 52 sum[col[u]]+=sz[u]-step; 53 } 54 int main() { 55 ios::sync_with_stdio(false);cin.tie(0); 56 int ca=0; 57 while(cin>>n){ 58 init(); 59 LL ct=0; 60 for(int i=1;i<=n;i++) { 61 cin>>col[i]; 62 if(!vis[col[i]]){ct++; vis[col[i]]=1;} 63 } 64 for(int i=0;i<n-1;i++){ 65 int x,y; 66 cin>>x>>y; 67 p[x].push_back(y); 68 p[y].push_back(x); 69 } 70 dfs(1,0); 71 for(int i=1;i<=n;i++){ 72 if(vis[i]&&i!=col[1]){ 73 LL szv=n-sum[i]; 74 cut=cut+szv*(szv-1)/2; 75 } 76 } 77 LL ans=n*(n-1)/2*ct; 78 cout<<"Case #"<<++ca<<": "<<ans-cut<<endl; 79 } 80 return 0; 81 }