PA
【题目描述】
汉诺塔升级了:现在我们有N个圆盘和N个柱子,每个圆盘大小都不一样,大的圆盘不能放在小的圆盘上面,N个柱子从左到右排成一排。每次你可以将一个柱子上的最上面的圆盘移动到右边或者左边的柱子上 (如果移动之后是合法的话) 。 现在告诉你初始时的状态, 你希望用最少的步数将第i小的盘子移动到第i根柱子上,问最小步数。
【输入格式】
第一行一个正整数T,代表询问的组数。
接下来T组数据,每组数据第一行一个整数N。
接下来一行每行N个正整数,代表每个柱子上圆盘的大小。
【输出格式】
输出共N行,代表每次的答案。如果方案不存在,输出“−1” 。
【样例输入】
4
3
2 1 3
2
7 8
2
10000 1000
3
97 96 95
【样例输出】
4
0
-1
20
【样例解释】
无。
【数据范围与规定】
对于70%的数据,N的值都是相等的。
对于100%的数据,1 ≤ T≤ 6 × 10e3 ,1 ≤ n ≤ 7。
【题目分析】
Bfs 因为很多很多数据 所以预处理所有的情况 然后O(1)查询
预处理的时候 1到7的都处理了
先存进去的 1 12 123 1234 12345 123456 1234567
这几个 然后把他拆成数组 place[i]表示第i小的在哪
因为移动的时候先动每个柱子最顶端的 所以维护top[i]表示i柱子最上面一个是谁
然后每个状态枚举移动那个 左移还是右移
那个bat数组是转移的时候简化操作用的
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=10000000; int n,top[10],place[10],res[maxn],q[maxn],bit[10],front,tail,w[10],z[10]; bool use[maxn]; bool cmp(int a,int b) { return w[a]<w[b]; } void analyze(int s) { int x=0; int ss=s; for (int a=1;a<=7;a++) top[a]=0; while (ss) { x++; place[x]=ss%10; ss/=10; } reverse(place+1,place+x+1); for (int a=x;a>=1;a--) top[place[a]]=a; for (int a=1;a<=x;a++) if (a==top[place[a]]) { int p=place[a]; if (p!=1 && (a<top[p-1] || !top[p-1])) { int news=s-bit[x-a]; if (!use[news]) { q[++tail]=news; use[news]=true; res[news]=res[s]+1; } } if (p!=x && (a<top[p+1] || !top[p+1])) { int news=s+bit[x-a]; if (!use[news]) { q[++tail]=news; use[news]=true; res[news]=res[s]+1; } } } } int main() { freopen("huakai.in","r",stdin); freopen("huakai.out","w",stdout); front=1,tail=0; int status=0; bit[0]=1; for (int a=1;a<=7;a++) { bit[a]=bit[a-1]*10; status=status*10+a; q[++tail]=status; use[status]=true; } for (;front<=tail;) { int s=q[front++]; analyze(s); } int t; scanf("%d",&t); for (;t--;) { scanf("%d",&n); for (int a=1;a<=n;a++) scanf("%d",&w[a]),z[a]=a; sort(z+1,z+n+1,cmp); int s=0; for (int a=1;a<=n;a++) s=s*10+z[a]; if (!use[s]) printf("-1 "); else printf("%d ",res[s]); } return 0; }
青春
【问题描述】
现在有一个被1× 1的小格子分割的矩形纸片,每个小格子内包含一个整数。现在你可以进行一系列的折叠, 每次折叠的折痕必须是分割两行或者两列小格子的分割线。在折叠完之后,所有重叠的小格子被看作一个单独的格子,并且这个格子的价值为重叠的小格子的价值和。你想要知道,在所有可能得到的新格子中,格子价值的最大值为多少。
【输入格式】
输入文件的第一行有两个整数N和M,分别表示初始的矩形纸片的长和宽。接下来的N行,每行有M个数字表示初始的小格子内的整数。
【输出格式】
输出一行表示所能得到的格子价值的最大值。
【样例输入】
2 2
1 -2
3 -4
【样例输出】
4
【样例解释】
无。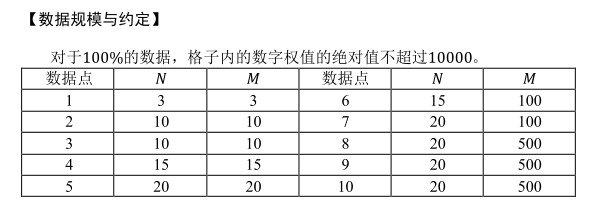
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; const int N=40; const int M=510; const int INF=0x3f3f3f3f; int n,m,z[N][M],sum[M],f[M],ans; void solve(int pos) { for(int i=1;i<=m;i++) sum[i]+=z[pos][i]; int maxv[2]={-INF,-INF}; for(int i=1;i<=m;i++) { f[i]=sum[i]; if(maxv[(i&1)^1]>0) f[i]+=maxv[(i&1)^1]; maxv[i&1]=max(maxv[i&1],f[i]); ans=max(ans,f[i]); } for(int i=pos+1;i<=n;i+=2) solve(i); for(int i=1;i<=m;i++) sum[i]-=z[pos][i]; } int main() { freopen("taritari.in","r",stdin); freopen("taritari.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&z[i][j]); ans=-INF; memset(sum,0,sizeof sum); for(int i=1;i<=n;i++) solve(i); printf("%d ",ans); }
三部曲
【问题描述】
因为外来的入侵,国王决定在某些城市加派士兵。所有城市初始士兵数量为0。当城市i被加派了k名士兵时。城市?的所有子城市需要被加派k + 1名士兵。这些子城市的所有子城市需要被加派k +2名士兵。以此类推。当然,加派士兵的同时,国王也需要不断了解当前的情况。于是他随时可能询问以城市 i 为根的子树中的所有城市共被加派了多少士兵。你现在是国王的军事大臣,你能回答出国王的每个询问么?
【输入格式】
第一行,包含两个整数N,P代表城市数量以及国王的命令的数量。
第二行N −1个整数,表示2− N号每个节点的父亲节点。
接下来的P行,每行代表国王的一个命令,命令分两种:
A X K在城市X加入K个士兵
Q X 询问以城市X为根的子树中所有士兵数量的和。
【输出格式】
对于每个Q,输出答案。
【样例输入】
7 10
1 1 2 2 5 5
Q 1
A 2 1
Q 1
Q 2
Q 5
A 5 0
Q 5
A 3 1
Q 1
Q 2
【样例输出】
0
11
11
8
10
14
13
【样例解释】
无。
【数据规模与约定】
对于50%的数据,1 ≤ N ≤ 1000 1≤ P<= 300。
对于100%的数据,1 ≤ N ≤ 50000 ,1≤ P ≤ 100000 1≤ X ≤ N 0 ≤ K ≤1000
【题目分析】
50分 暴力解决 vector建图
#include<cstdio> #include<cstring> #include<iostream> #include<vector> using namespace std; #define maxn 50010 #define maxm 100010 vector<int>tu[maxn]; int ans[maxn]={0}; int n,p; int sum=0; void print(int a) { for(int i=0;i<tu[a].size();i++) { sum+=ans[tu[a][i]]; if(tu[tu[a][i]].size()) print(tu[a][i]); } } void add(int a,int b) { for(int i=0;i<tu[a].size();i++) { int tp=tu[a][i]; ans[tp]+=b; if(tu[tp].size()) add(tp,b+1); } } int main() { freopen("truetears.in","r",stdin); freopen("truetears.out","w",stdout); scanf("%d%d",&n,&p); for(int i=2;i<=n;i++) { int a; scanf("%d",&a); tu[a].push_back(i); } for(int i=1;i<=p;i++) { char x;int y,z; cin>>x; if(x=='Q') { sum=0; scanf("%d",&y); if(tu[y].size()) print(y); sum+=ans[y]; printf("%d ",sum); } if(x=='A') { scanf("%d%d",&y,&z); ans[y]+=z; if(tu[y].size()) add(y,z+1); } } fclose(stdin);fclose(stdout); return 0; }