1、题目
给定 n 个数组成的一个数列,规定有两种操作,一是修改某个元素,二是求子数列 [a,b] 的连续和。
输入格式
第一行包含两个整数 n 和 m,分别表示数的个数和操作次数。
第二行包含 n 个整数,表示完整数列。
接下来 m 行,每行包含三个整数 k,a,b (k=0,表示求子数列[a,b]的和;k=1,表示第 a 个数加 b)。
数列从 1 开始计数。
输出格式
输出若干行数字,表示 k=0 时,对应的子数列 [a,b] 的连续和。
数据范围
[1≤n≤100000,
1≤m≤100000,
1≤a≤b≤n
]
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
1 1 5
0 1 3
0 4 8
1 7 5
0 4 8
输出样例:
11
30
35
2、题意分析
1、知识点
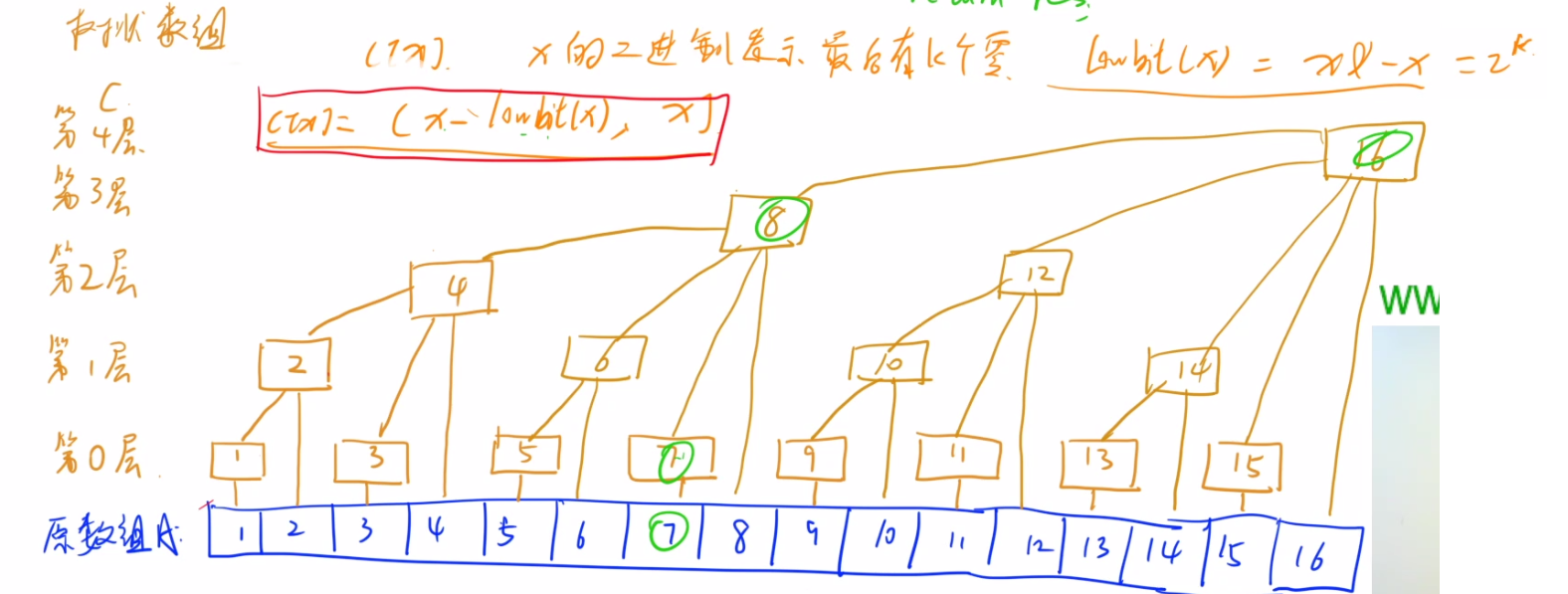
本题考查树状数组的使用、树状数组用起来的时间复杂度为O(logn)、操作一共有以下两种:
1、给某个位置上的数加上一个数
void add(int x, int v)
{
for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}
2、求某一个前缀和
int query(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
3、附加lowbit操作
int lowbit(int x)
{
return x & -x;
}
2、具体分析(略)
3、代码
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100010;
int a[N], tr[N];
int n, m;
int lowbit(int x)
{
return x & -x;
}
void add(int x, int v)
{
for(int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}
int query(int x)
{
int res = 0;
for(int i = x; i ; i -= lowbit(i)) res += tr[i];
return res;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n ; i ++) scanf("%d", &a[i]);
for(int i = 1; i <= n ; i ++) add(i, a[i]);
while(m --)
{
int k, x, y;
scanf("%d%d%d", &k, &x, &y);
if(k == 0) printf("%d
", query(y) - query(x - 1));
else add(x, y);
}
return 0;
}