动态规划-线性DP&区间DP

数字三角形

题意

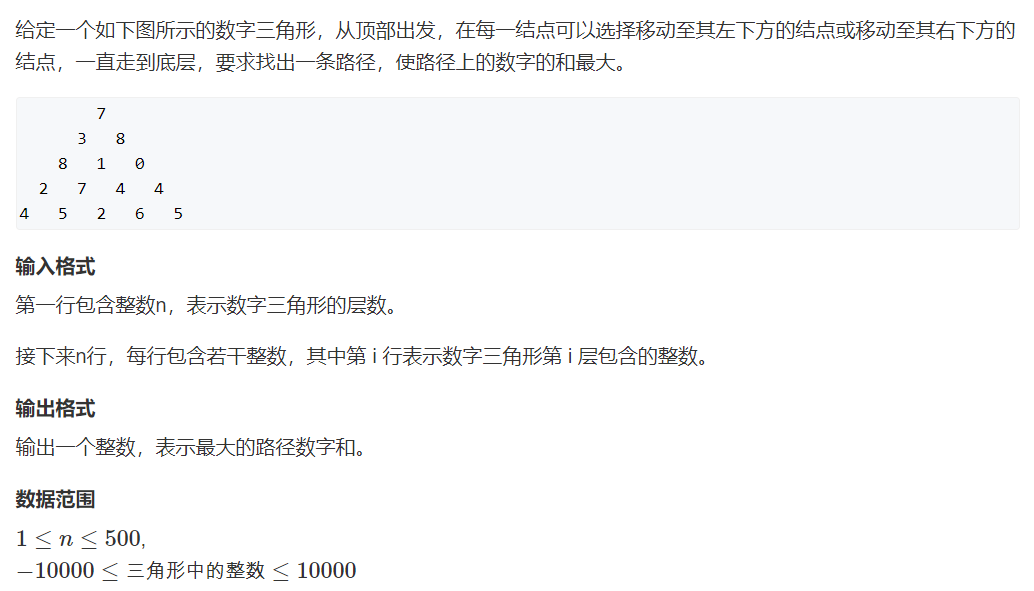
算法思路

从倒数第二层向上，更新每层数的最大值，取决于其下一层的左右那个最大，一直更新知道最顶层，即可。

#include<bits/stdc++.h>
using namespace std;
int f[510][510];

int main()
{
    int i,j,n;
    cin>>n;
    for(i=0;i<n;i++)
    {
        for(j=0;j<=i;j++)
        cin>>f[i][j];
    }
    for(i=n-2;i>=0;i--)
    {
        for(j=0;j<=i;j++)
            f[i][j]+=max(f[i+1][j],f[i+1][j+1]);
    }
    cout<<f[0][0]<<endl;
    return 0;
}

最长上升子序列

题意

算法思路 

f数组存储当前最长递增子序列，当遍历过程中的a数组的值大于f数组当前最后存储的数值，则直接将a数组当前值放到f数组后，若小于，则二分查找第一个小于a数组当前值的下标，进行替换。

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int a[N];
int f[N];

int main()
{
    int i,j,n;
    cin>>n;
    for(i=1;i<=n;i++)
        cin>>a[i];
    int cnt=0;
    f[++cnt]=a[1];
    for(i=2;i<=n;i++)
    {
        if(a[i]>f[cnt])
            f[++cnt]=a[i];
        else
        {
            int k=lower_bound(f+1,f+cnt+1,a[i])-f;
            f[k]=a[i];
        }
    }
    cout<<cnt;
    return 0;
}

最长公共子序列

题意

算法思路 

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N][N];
int main()
{
    int i,j,n,m;
    char a[N],b[N];
    cin>>n>>m;
    cin>>a+1;
    cin>>b+1;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=m;j++)
        {
            if(a[i]==b[j])
                f[i][j]=f[i-1][j-1]+1;
            else
                f[i][j]=max(f[i-1][j],f[i][j-1]);
        }
    }
    cout<<f[n][m];
    return 0;
}

编辑距离

题意

 算法思路

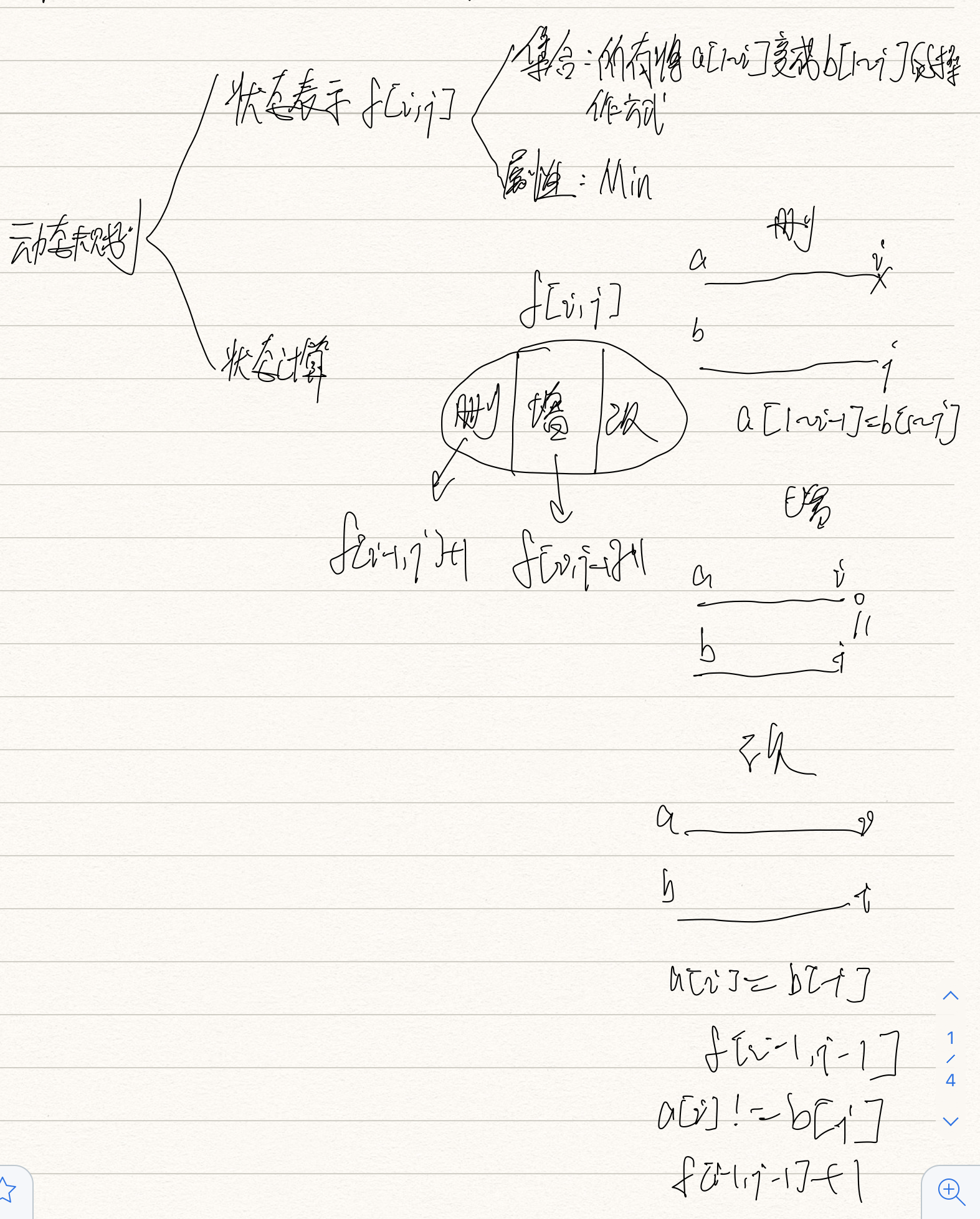
#include<bits/stdc++.h>
using namespace std;
int f[20][20];

int editx(char a[],char b[])
{
    int i,j;
    int len1=strlen(a+1);
    int len2=strlen(b+1);
    for(i=1;i<=len1;i++)
        f[i][0]=i;
    for(i=1;i<=len2;i++)
        f[0][i]=i;
    for(i=1;i<=len1;i++)
    {
        for(j=1;j<=len2;j++)
        {
            f[i][j]=min(f[i-1][j],f[i][j-1])+1;
            f[i][j]=min(f[i][j],f[i-1][j-1]+(a[i]!=b[j]));
        }
    }
    return f[len1][len2];
}

int main()
{
    int i,j,n,m;
    char c[1010][20];
    cin>>n>>m;
    for(i=0;i<n;i++)
        cin>>c[i]+1;
    while(m--)
    {
        char t[20];
        int num;
        cin>>t+1>>num;
        int ans=0;
        for(i=0;i<n;i++)
        {
            if(editx(c[i],t)<=num)
                ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

区间dp-石子合并

题意

 算法思路

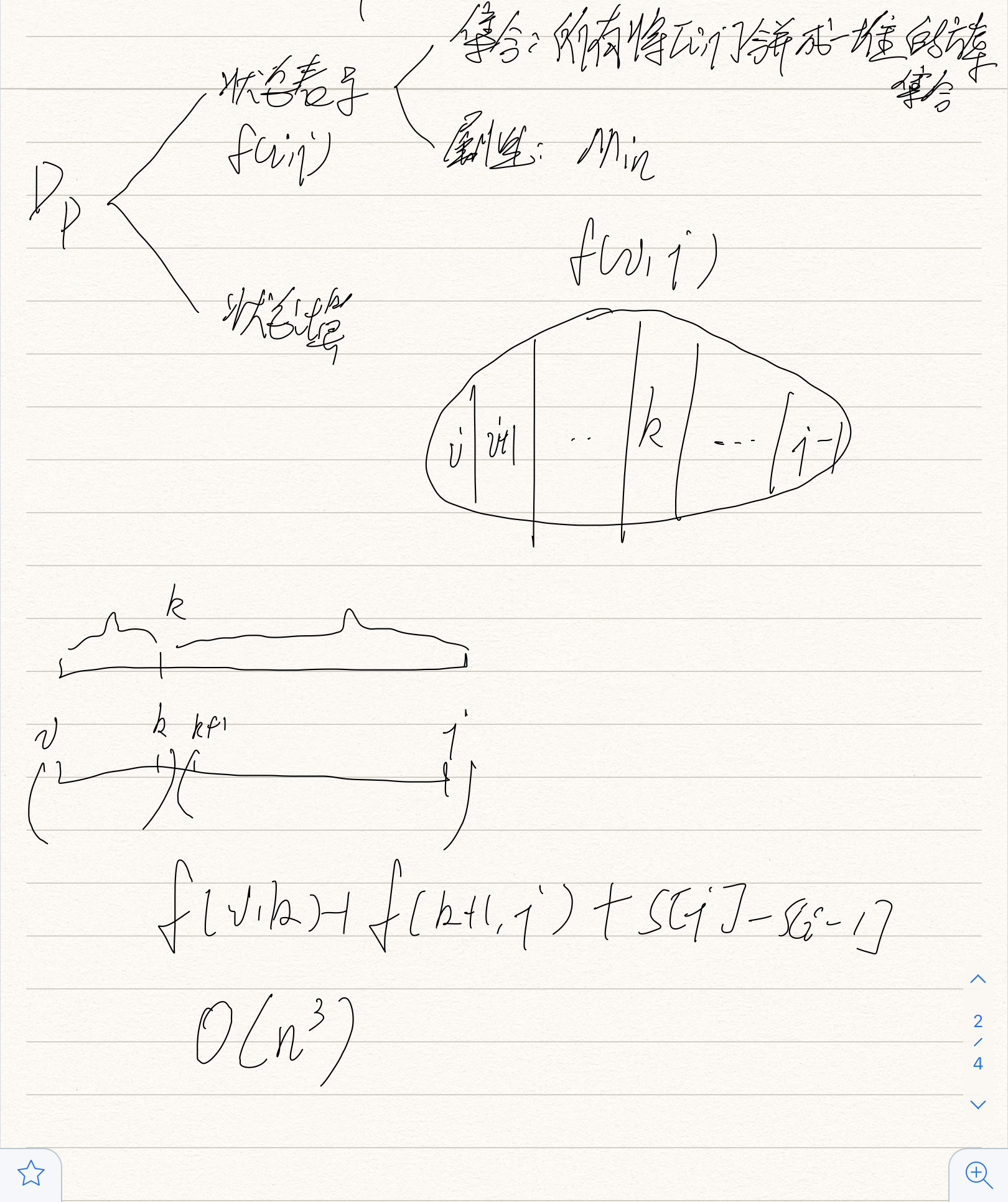
#include<bits/stdc++.h>
using namespace std;
const int N=330;
int dp[N][N];
int a[N];
int s[N];
int main()
{
    int i,j,n,len,k;
    cin>>n;
    for(i=1;i<=n;i++)
    {
        cin>>a[i];
        s[i]=s[i-1]+a[i];
    }
    for(len=2;len<=n;len++)
    {
        for(i=0;i+len-1<=n;i++)
        {
            int j=i+len-1;
            dp[i][j]=1e8;
            for(k=i;k<j;k++)
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
        }
    }
    cout<<dp[1][n]<<endl;
    return 0;
}