1》递归相关:
递归:递归算法是一种直接或间接地调用自身算法的过程,在计算机编写程序中,递归算法对解决一大类问题是十分有效的,它往往使算法的描述简洁而且 易于理解;
特点:
(1)递归就是在过程或函数中调用自身;
(2)在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口;
(3)递归算法解题通常显得很简洁,但递归算法解题的运行效率较低,所以一般不提倡使用递归算法设计程序;
(4)在递归调用的过程当中系统为每一层的返回点,局部量等开辟了栈来存储,递归次数过多容易造成栈溢出等,所以一般不提倡使用递归算法设计 程序;
要求:
递归算法所体现的“重复”一般有三个要求:
(1)每次调用在规模上都有所缩小(通常是减半);
(2)相邻两次重复直接有紧密的联系,前一次要为后一次做准备(通常前一次的输出就作为后一次的输入);
(3)在问题的规模极小时必须用直接给出解答而不再进行递归调用,因而每次递归调用都是有条件的(以规模未达到直接解答的大小为条件),无条 件递归调用将会成为死循环而不能正常结束;
示例:

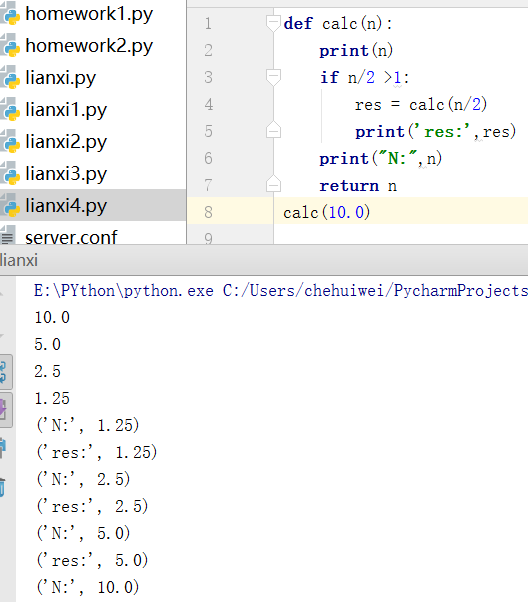
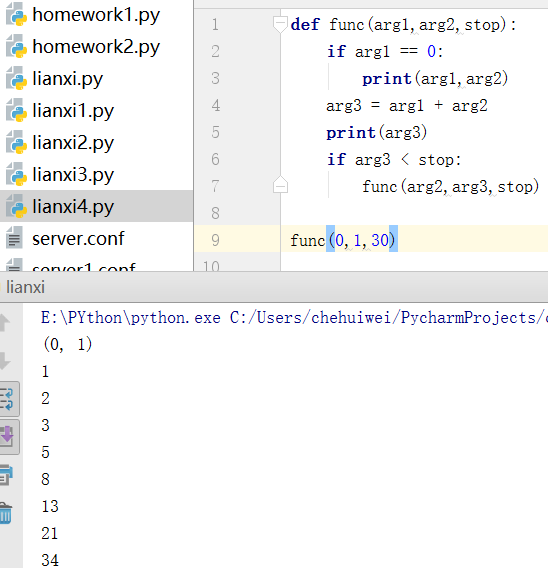
2》通过递归实现裴波那契数列(每个数总是等于前两个数的值的数列):
3》算法基础之二分查找:

上图会找不到1,现做出改正:
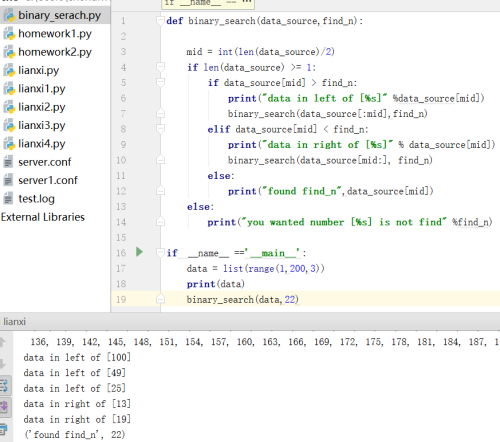
4》算法基础之二维数组:
1>生成列表方法:

2>生成二维数组方法:

eg:将一个二维数组翻转90度:
自己做的:
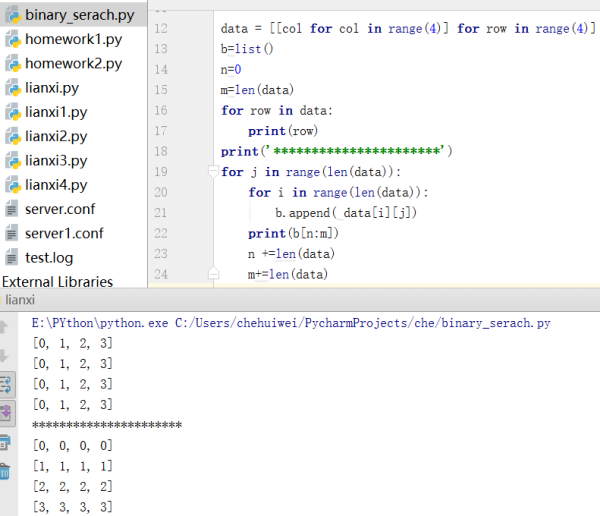
参考老师代码:

5》算法基础之冒泡排序:
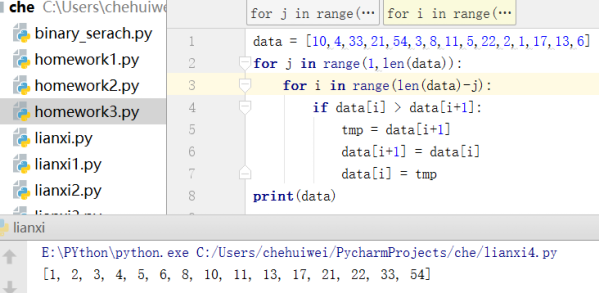
6》时间复杂度介绍:
1>时间频度:
一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机进行测试才能知道,当我们可能也没有必要对每个算法都上机测试,只需知道哪个算 法花费等待时间多,哪个算法花费的时间少就可以了;并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费 时间就多,一个算法中的语句执行次数称为语句频度或者时间频度,记为T(n);
2>时间复杂度:
在刚才提到的时间频度中,n称为问题的规模,当n不断变化时,时间频度T(n)也会不断变化;但有时我们也想指定它变化时呈现什么规律,为此,我们 引入时间复杂度概念;一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大 时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数,记作T(n)=O(f(n)),称O(f(n))为算法的渐进时
间复杂度,简称时间复杂度;
3>指数时间:
指的是一个问题求解所需要的计算时间m(n),依输入数据的大小n而呈指数成长(即输入数据的数量依线性成长,所花的时间将会以指数成长)
4>示例:
第一个for循环的时间复杂度为O(n),第二个for循环的时间复杂度为O(n^2),则整个算法的时间复杂度为O(n+n^2)=O(n^2); 
5>常数时间:
若对于一个算法,T(n)的上界与输入大小无关,则称其具有常数时间,记作O(1)时间;一个例子是访问数组中的单个元素,因为访问它只需要一条指 令,但是,找到无序数组中的最小元素则不是,因为这需要遍历所有元素找到最小值,这是一项线性时间的操作,或称O(n)时间;但如果预先知道元素的数 量并假设数量保持不变,则该操作也可被称为具有常数时间;
6>对数时间:
若算法的T(n)=O(log n),则称其具有对数时间;常见的具有对数时间的算法有二叉树的相关操作和二分搜索;对数时间的算法是非常有效的,因为每增加 一个输入,其所需要的额外计算时间会变小;递归将字符串砍半并且输出是这个类别函数的一个简单例子;
7>线性时间:
如果一个算法的时间复杂度为O(n),则称这个算法具有线性时间,或O(n)时间,非正式地说,这意味着
对于足够大的输入,运行时间增加的大小与输入成线性关系。例如,一个计算列表所有元素的和的程序,需要的时间与列表的长度成正比;