[COJ6997]旅行商问题二
试题描述
Bob是一名旅行商,Bob同时也是一个哲学家,他深知到了一个地方就要掏出钱包把所有景点都玩到。一个城市有N个景点,其中N-1条无向道路链接成一个连通图。Bob出来带的经费是有限的,他希望从1号景点出发,把所有景点都走到(不必返回1点)。每个点不一定只走一次,但是要保证从一号点游览完所有景点的路程最小,他希望你告诉他这个路程。
输入
第一行:一个数N,表示有N个景点(包括1点)
下面N-1行:每行表示一条边,A,B,C表示A点到B点有一条长度为C的边。
输出
游览完所有点的最小路程。
输入示例
3 1 2 3 2 3 3
输出示例
6
数据规模及约定
N<=1000
题解
搞一个树形 dp,设 f(i) 表示对于子树 i,遍历一遍所有节点但不回到节点 i 的最短路长度;g(i) 表示遍历一遍子树 i 且回到节点 i 的最短长度。
那么显然
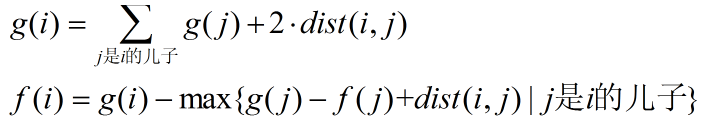
最后答案是 f(1)。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <stack>
#include <vector>
#include <queue>
#include <cstring>
#include <string>
#include <map>
#include <set>
using namespace std;
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 1010
#define maxm 2010
int n, m, head[maxn], next[maxm], to[maxm], dist[maxm];
void AddEdge(int a, int b, int c) {
to[++m] = b; dist[m] = c; next[m] = head[a]; head[a] = m;
swap(a, b);
to[++m] = b; dist[m] = c; next[m] = head[a]; head[a] = m;
return ;
}
int f[maxn], g[maxn];
void dp(int u, int fa) {
g[u] = 0;
int tmp = 0;
for(int e = head[u]; e; e = next[e]) if(to[e] != fa) {
dp(to[e], u);
g[u] += g[to[e]] + 2 * dist[e];
tmp = max(tmp, g[to[e]] - f[to[e]] + dist[e]);
}
f[u] = g[u] - tmp;
return ;
}
int main() {
n = read();
for(int i = 1; i < n; i++) {
int a = read(), b = read(), c = read();
AddEdge(a, b, c);
}
dp(1, 0);
printf("%d
", f[1]);
return 0;
}
并不知道数据范围为什么这么小