一、概念
1、浮点数:小数点位置是漂浮不定的。
例如:浮点数运算 1.1 * 1.1 = 1.21,小数点位置发生了变化。
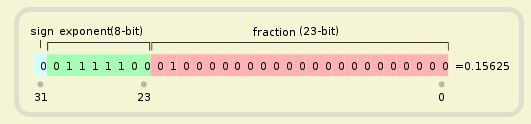
IEEE 754 规定,浮点数的表示方法为:
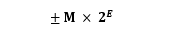
最高的 1 位是符号位 s,接着的 8 位是指数E,剩下的 23 位为有效数字 M。
2、定点数:小数点的位置是确定的。
例如:定点数运算 1.1 * 1.1 = 1.2,小数点的位置没有变化。
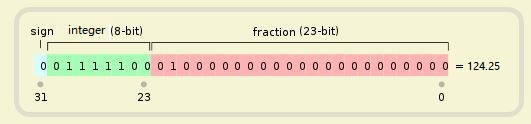
定点的意思是,小数点固定在 32 位中的某个位置,前面的是整数,后面的是小数。
小数点具体固定在哪里,可以自己在程序中指定。
二、Verilog表示定点数
FPGA 的寄存器只可以表示正整数,通过约定【最高位为符号位】则可以表达负整数了。同理,带小数点的定点数也是可以通过一些约定来表示。
约定方法:确定小数点的位置。如下图所示,Qn表示小数点的位置,n为多少表示有多少位小数,看看同样的二进制数字“10101”会变成什么。
二进制数 小数点位置 对应定点数 10101 Q0 10101 10101 Q1 1010.1 10101 Q2 101.01 10101 Q3 10.101 10101 Q4 1.0101 10101 Q5 0.10101
因此我们只要定位了小数点位置后,就可以在FPGA中表达带小数的定点数。
三、浮点数的定点化
两个 16 位的浮点数运算,最高位是符号位: 2.918 * 3.1415926 = 9.1671672068,尝试将浮点数进行定点化。
1、定点转换(Qn=12)
符号1位,整数取3位(实际2位就够),小数12位,可以看成把 1 分成了 212份,因此:
- 2.918 * 212 = 11952.168 = 11952;
- 3.1415926 * 212 = 12867.8632896 = 12868;
2、定点数相乘
11952 * 12868 = 153798336。
3、结果还原
相乘后,整数部分为 6 位,小数部分为 24 位。因此结果 = 153798336 / 224 = 9.167095184326171875,和原计算值差距非常小。
4、量化误差和量化精度
小数点的位置不同带来的量化误差不同,例如上面定点转换的过程中出现的小数点进行了四舍五入,这是因为 2.918 无法完全用 1/212来表示。小数位数越多,表示的量化精度越高,小数位为 Qn,最大量化精度为 1/2n。
5、无损定点化
所谓【无损定点化】只是数学概念,只要量化误差小于精度的一半,就认为是“无损”的。按照这个标准,那对小数点采取四舍五入的结果必然是无损的。但是校招时很多题采取的是“量化后直接去除小数”,那么小数大于 0.5 则不是无损的了。
四、例题
1、【大疆】对 12.918 做无损定点化,需要的最小位宽是多少位?位宽选择 11 位时的量化误差是多少?
A 13位,0.0118 B 12位,0.0118 C 13位,0.0039 D 12位,0.0039
分析:(1)整数 12 需要 4bit。假设位宽选择12位,即小数需要 8bit,12.918 * 28 = 3307.008,定点化后的小数小于0.5,可以看成是【无损定点化】,固答案为 12 位;(2)位宽选择11位,即小数需要 7bit,12.918 * 27 = 1653.504,量化误差为 0.504/27 = 0.0039375,固答案为0.0039。
答案:结合分析,得出答案为D。
2、【大疆】对12.758做无损定点化,需要的最小位宽是多少位?位宽选择为8位时的量化误差是多少?
A 11位,0.008 B 11位,0.08 C 12位,0.008 D 12位,0.08
分析:(1)整数 12 需要 4bit。假设位宽选择11位,即小数需要 7bit,12.758 * 27 = 1633.024,定点化后的小数小于0.5,可以看成是【无损定点化】,固答案为 11 位;(2)位宽选择 8 位,即小数需要 4bit,12.758 * 24 = 204.128,量化误差为 0.128/24 = 0.008,固答案为0.008。
答案:结合分析,得出答案为A。
感觉这题的第一问有些毛病,位宽为 8 位时也符合【无损定点化】。我算了一下,位宽为 7 位(小数为3位)时仍然是【无损定点化】,位宽为 6 位时才不是【无损定点化】。但这是选择题,只能选 A 了。
参考资料:
http://fpgabbs.com/thread-771-1-1.html