唉,自从看了几天数论,发现每一次一看一个下午就过去了,今天把扩展欧几里得求逆元搞定之后,来恶补了一下欧拉函数和欧拉线性筛,就说一下今天的所得吧:
欧拉函数是什么?
在数论中,对正整数n,欧拉函数 是小于或等于n的正整数中与n互质的数的数目。(何为互质? 互质一般是指两个数的最大公约数为1即为互质)
是小于或等于n的正整数中与n互质的数的数目。(何为互质? 互质一般是指两个数的最大公约数为1即为互质)
一般欧拉函数都用“φ(n)=..”来表达
欧拉函数的基本要用到的性质有哪些?
一:
当φ(n)中的n为质数时,φ(n) = n - 1,因为当n为质数时,只有它本身与本身不互质。
二:
假如 m mod p = 0, 那么phi(m * p)=p * phi(m)。
证明:
假设 b = gcd (n,m) n,m不互质 ∴ n = k1·b , m = k2·b
∴ n+m = (k1+k2)b ∴n+m 与 m 不互质
[1,m]中与m不互质的整数n 共 m - φ(m) 个。
n+m与m不互质 ∴[1+m,m+m]即(m,2m]中与m不互质的整数也是m-φ(m)个
∴[1,m·p]中与m不互质的整数m·p-p·φ(m)个
∵[1,m·p]中与m·p不互质的整数熟练为m·p - p·φ(m) = m·p - φ(m·p)
∴φ(m·p) = p · φ(m)
三:若 m mod n !=0 ,那么 φ(m*n)=φ(m)*(n-1)=φ(m)*φ(n); 由此可看出
φ(m*n)为积性函数。
四: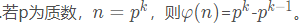
欧拉函数如何计算?
想详细了解的可以去参考https://blog.csdn.net/liuzibujian/article/details/81086324 liuzibujian大佬的博客(写的很清晰明了)。这里就简单给大家看一下:

说完了欧拉函数,我们就可以进一步去了解欧拉线性筛了!
欧拉线性筛的作用就是筛选一个范围内的所有合数(去掉),求出所有质数并且知道这个范围内的每个数字的欧拉函数。
由于很多大佬讲的不是很详细啊,并且我不是大佬,所以我各种总结各种调试尽量用最简单的讲法来理清楚欧拉筛到底是个什么东西。
我先说下原理吧,筛选出合数的部分大致跟我之前的博客说的素数筛选法很相似,不过这个是倍数筛选,比之前那个筛选法更快,利用最小质因子去筛选出所有合数并且标记。
代码如下(100以内的欧拉筛):
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<malloc.h> 5 #include<memory.h> 6 #include<conio.h> 7 using namespace std; 8 9 int phi[101], prime[101]; 10 bool p[101]; 11 12 int main() { 13 memset(p, true, sizeof(p)); 14 int cnt = 0; 15 phi[1] = 1; 16 for (int i = 2; i <= 100; ++i) { 17 if (p[i]) { 18 prime[++cnt] = i;//2,3,5,7 19 } 20 for (int j = 1; j <= cnt && prime[j] * i <= 100; ++j) 21 { 22 p[prime[j] * i] = false; 23 24 if (i%prime[j] == 0) break; 25 } 26 } 27 28 for (int i = 2; i <= 100; i++) 29 if (p[i])cout << i << endl; 30 _getch(); 31 return 0; 32 }
一点一点说吧,首先是3个数组phi[],prime[],p[],它们三个的作用分别是存欧拉函数,存质数,筛选。
第一步:我们把bool类型的 p数组 全部初始化为true
第二步:进入第一个for循环,第一个if 判断i是否为质数,若为质数则存入prime[](第一次看的人可能会问,为什么一开始就去判断p[i],p[i]不全部是true吗,那不是所有数都存进去了?但请不要急,一开始我就说了,这是利用最小质因子去筛选出所有合数,标记成false,2是质数对吧?那么从2开始筛选,是不是进入第二个for循环中后,p[prime[j]*i]就把4给筛选出来了,一次类推,后面6也会被3给筛选出来,那么是质数的依然是true,是合数的是不是都变成了false了?)
第三步:进入第二个循环,筛选阶段,p[prime[j]*i]在第二步已经解释过了,那么 if(i%prime[j]==0) break;是什么意思呢?还是那个重点,就是要求每一个合数都要由它的最小质因数筛去。假设当前的I是prime[j]的倍数,那么i=n×prime[j] (n∈N*)一定成立。如果不现在不跳出循环,当到prime[j+1]时,i也会筛去I×prime[j+1],由于i=n×prime[j],所以I×prime[j+1]=n×prime[j]×prime[j+1],这就不是我们要的最小质因数了,就会多出很多不需要的步骤,提高复杂度。
OK,筛选我们已经会了,接下来就是求欧拉函数了~
代码如下:
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<malloc.h> 5 #include<memory.h> 6 #include<conio.h> 7 using namespace std; 8 9 int phi[101], prime[101]; 10 bool p[101]; 11 12 int main() { 13 memset(p, true, sizeof(p)); 14 int cnt = 0; 15 phi[1] = 1; 16 for (int i = 2; i <= 100; ++i) { 17 if (p[i]) { 18 prime[++cnt] = i; 19 phi[i] = i - 1; 20 } 21 for (int j = 1; j <= cnt && prime[j] * i <= 100; ++j) 22 { 23 p[prime[j] * i] = false; 24 25 if (i%prime[j] == 0) 26 { 27 phi[i*prime[j]] = prime[j] * phi[i]; 28 break; 29 } 30 else { 31 phi[i*prime[j]] = phi[i] * phi[prime[j]]; 32 } 33 } 34 } 35 36 //for (int i = 2; i <= 100; i++) 37 //if (p[i])cout << i << endl; 38 for (int j = 1; j <= 100; j++) 39 cout << phi[j] << endl; 40 _getch(); 41 return 0; 42 }
其实就是在原代码上多了几行改动,第一是判断质数的语句中多了phi[i] = i - 1; 之前说过了 若n为质数,那么对应的φ(n) = n - 1,第二是最小质因子筛选的过程中,由之前的第二条性质和第三条性质可知,prime[j]为质数,i为任意数,且 i%prime[j] == 0的话,那么phi(m * p)=p * phi(m)。(p为质数),若i%prime[j]!=0的话,phi[i*prime[j]] = phi[i] * phi[prime[j]];,这样就保证了phi中的每一个值都会更新。对于特殊情况phi[1],我们必须直接使phi[1]=1,因为1既不是合数也不是质数,但按照国际要求来,1的欧拉函数为1.
综上所述,我们就完成了所有的步骤了,这就是欧拉线性筛的作用了,大家应该能看懂,毕竟我太菜了。
---------------------------------------------------------------------------------------------------
