实面试题之:Hashmap的结构,1.7和1.8有哪些区别
不同点:
(1)JDK1.7用的是头插法,而JDK1.8及之后使用的都是尾插法,那么他们为什么要这样做呢?因为JDK1.7是用单链表进行的纵向延伸,当采用头插法时会容易出现逆序且环形链表死循环问题。但是在JDK1.8之后是因为加入了红黑树使用尾插法,能够避免出现逆序且链表死循环的问题。
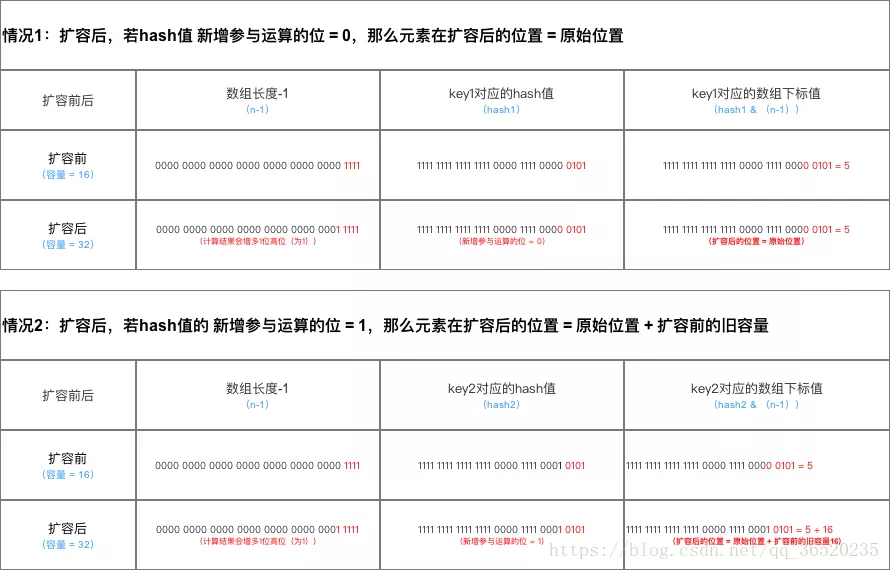
(2)扩容后数据存储位置的计算方式也不一样:
- 在JDK1.7的时候是直接用hash值和需要扩容的二进制数进行&(这里就是为什么扩容的时候为啥一定必须是2的多少次幂的原因所在,因为如果只有2的n次幂的情况时最后一位二进制数才一定是1,这样能最大程度减少hash碰撞)(hash值 & length-1)
- 而在JDK1.8的时候直接用了JDK1.7的时候计算的规律,也就是扩容前的原始位置+扩容的大小值=JDK1.8的计算方式,而不再是JDK1.7的那种异或的方法。但是这种方式就相当于只需要判断Hash值的新增参与运算的位是0还是1就直接迅速计算出了扩容后的储存方式。
在计算hash值的时候,JDK1.7用了9次扰动处理=4次位运算+5次异或,而JDK1.8只用了2次扰动处理=1次位运算+1次异或。
扩容流程对比图:
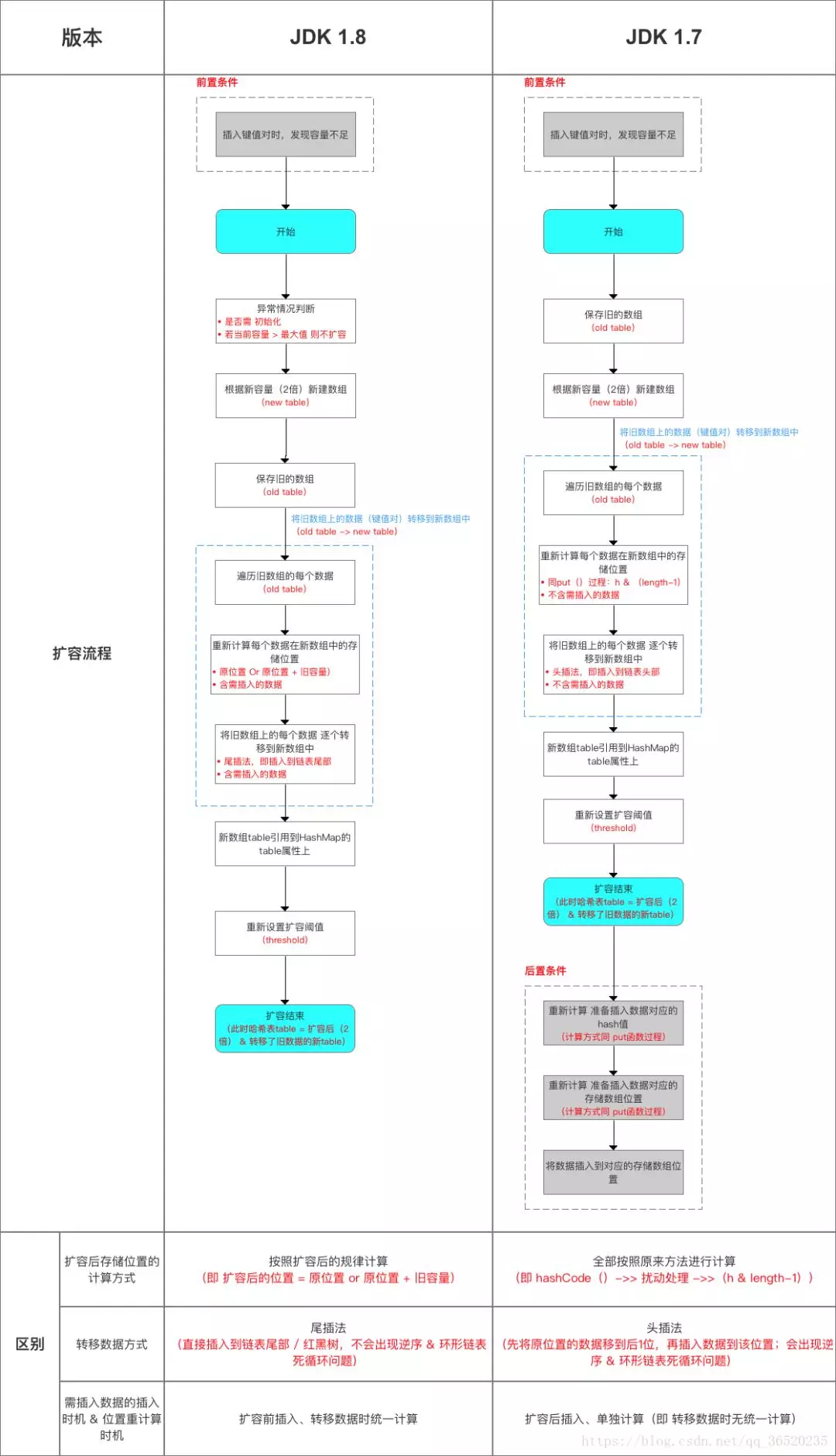
(3)JDK1.7的时候使用的是数组+ 单链表的数据结构。但是在JDK1.8及之后时,使用的是数组+链表+红黑树的数据结构(当链表的深度达到8的时候,也就是默认阈值,就会自动扩容把链表转成红黑树的数据结构来把时间复杂度从O(n)变成O(logN)提高了效率)
这里再进行补充两个问题:
(1)为什么在JDK1.7的时候是先进行扩容后进行插入,而在JDK1.8的时候则是先插入后进行扩容的呢?
//其实就是当这个Map中实际插入的键值对的值的大小如果大于这个默认的阈值的时候(初始是16*0.75=12)的时候才会触发扩容, //这个是在JDK1.8中的先插入后扩容 if (++size > threshold) resize();
其实这个问题也是JDK8对HashMap中,主要是因为对链表转为红黑树进行的优化,因为你插入这个节点的时候有可能是普通链表节点,也有可能是红黑树节点,但是为什么1.8之后HashMap变为先插入后扩容的原因,我也有点不是很理解?欢迎来讨论这个问题?
但是在JDK1.7中的话,是先进行扩容后进行插入的,就是当你发现你插入的桶是不是为空,如果不为空说明存在值就发生了hash冲突,那么就必须得扩容,但是如果不发生Hash冲突的话,说明当前桶是空的(后面并没有挂有链表),那就等到下一次发生Hash冲突的时候在进行扩容,但是当如果以后都没有发生hash冲突产生,那么就不会进行扩容了,减少了一次无用扩容,也减少了内存的使用
void addEntry(int hash, K key, V value, int bucketIndex) { //这里当钱数组如果大于等于12(假如)阈值的话,并且当前的数组的Entry数组还不能为空的时候就扩容 if ((size >= threshold) && (null != table[bucketIndex])) { //扩容数组,比较耗时 resize(2 * table.length); hash = (null != key) ? hash(key) : 0; bucketIndex = indexFor(hash, table.length); } createEntry(hash, key, value, bucketIndex); } void createEntry(int hash, K key, V value, int bucketIndex) { Entry<K,V> e = table[bucketIndex]; //把新加的放在原先在的前面,原先的是e,现在的是new,next指向e table[bucketIndex] = new Entry<>(hash, key, value, e);//假设现在是new size++; }
2)为什么在JDK1.8中进行对HashMap优化的时候,把链表转化为红黑树的阈值是8,而不是7或者不是20呢(面试蘑菇街问过)?
如果选择6和8(如果链表小于等于6树还原转为链表,大于等于8转为树),中间有个差值7可以有效防止链表和树频繁转换。假设一下,如果设计成链表个数超过8则链表转换成树结构,链表个数小于8则树结构转换成链表,如果一个HashMap不停的插入、删除元素,链表个数在8左右徘徊,就会频繁的发生树转链表、链表转树,效率会很低。
还有一点重要的就是由于treenodes的大小大约是常规节点的两倍,因此我们仅在容器包含足够的节点以保证使用时才使用它们,当它们变得太小(由于移除或调整大小)时,它们会被转换回普通的node节点,容器中节点分布在hash桶中的频率遵循泊松分布,桶的长度超过8的概率非常非常小。所以作者应该是根据概率统计而选择了8作为阀值
//Java中解释的原因 * Because TreeNodes are about twice the size of regular nodes, we * use them only when bins contain enough nodes to warrant use * (see TREEIFY_THRESHOLD). And when they become too small (due to * removal or resizing) they are converted back to plain bins. In * usages with well-distributed user hashCodes, tree bins are * rarely used. Ideally, under random hashCodes, the frequency of * nodes in bins follows a Poisson distribution * (http://en.wikipedia.org/wiki/Poisson_distribution) with a * parameter of about 0.5 on average for the default resizing * threshold of 0.75, although with a large variance because of * resizing granularity. Ignoring variance, the expected * occurrences of list size k are (exp(-0.5) * pow(0.5, k) / * factorial(k)). The first values are: * * 0: 0.60653066 * 1: 0.30326533 * 2: 0.07581633 * 3: 0.01263606 * 4: 0.00157952 * 5: 0.00015795 * 6: 0.00001316 * 7: 0.00000094 * 8: 0.00000006 * more: less than 1 in ten million
二、哈希表如何解决Hash冲突
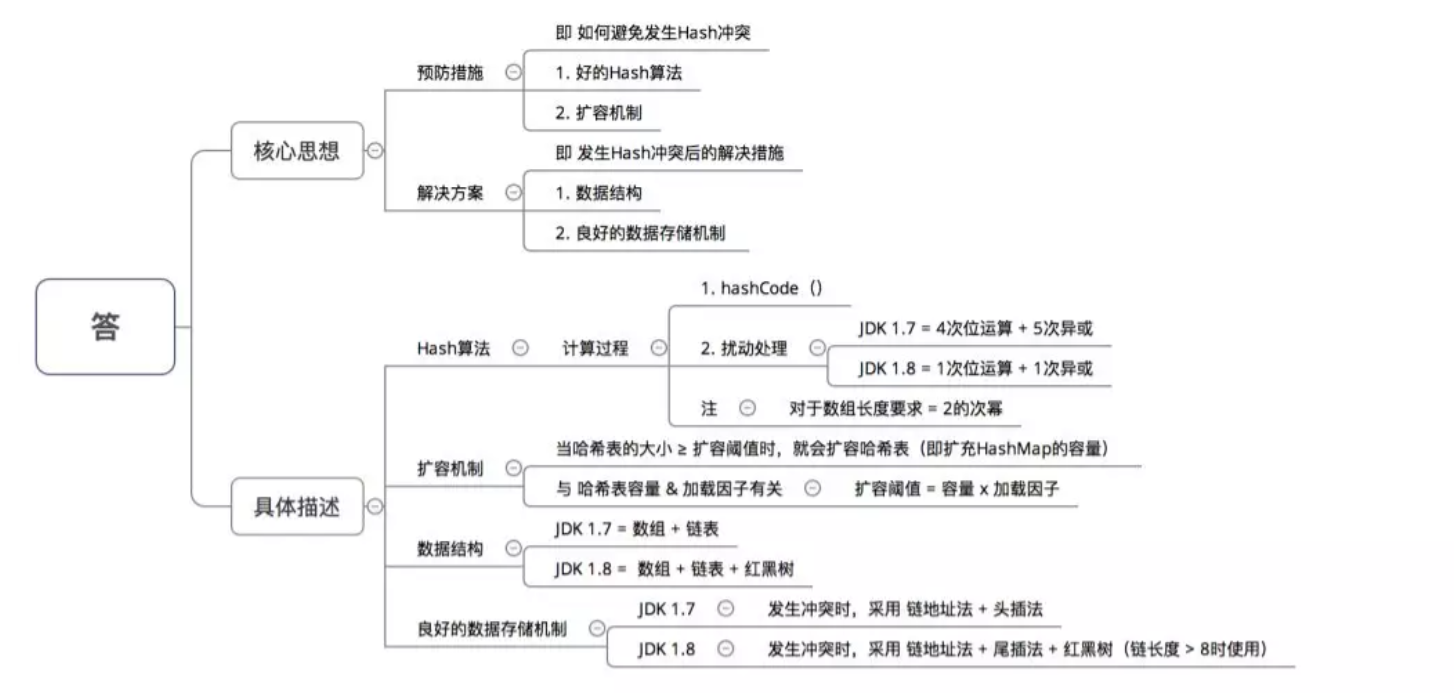
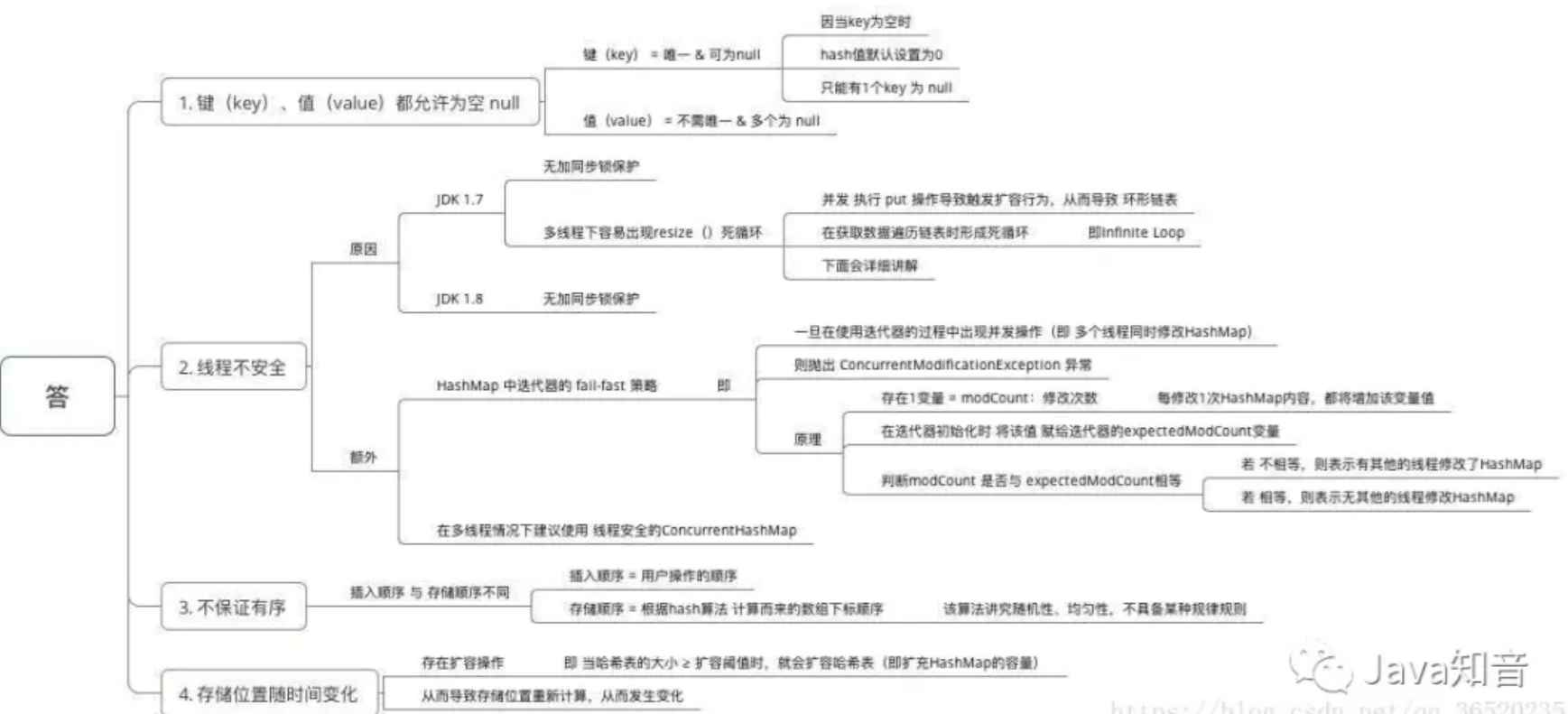
三、为什么HashMap具备下述特点:键-值(key-value)都允许为空、线程不安全、不保证有序、存储位置随时间变化
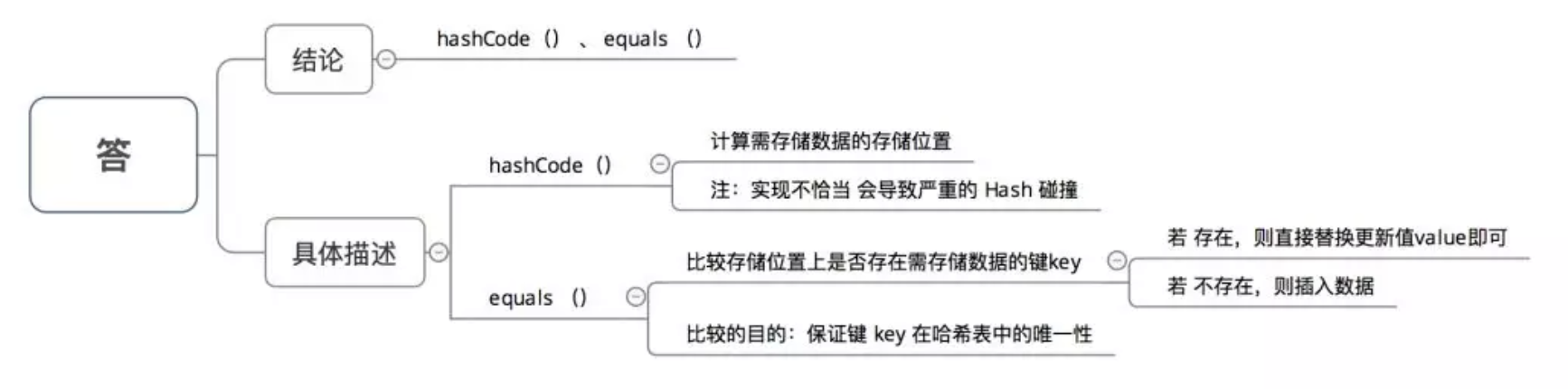
四、为什么 HashMap 中 String、Integer 这样的包装类适合作为 key 键

五、HashMap 中的 key若 Object类型, 则需实现哪些方法?