无向图—深度优先和广度优先算法极其应用

首先在这里介绍下Algorithms这个网站第二部分，是Algorithms这本书的在线课程。

另外Coursera上的图上的算法的这个课程也很不错。

 

图的几种表示方法：

用那种方式（数据结构）表示图，这包含以下两个要求：（1） 空间要合适  （2）实例的方法的实现一定要快

那么有三种可供选择：

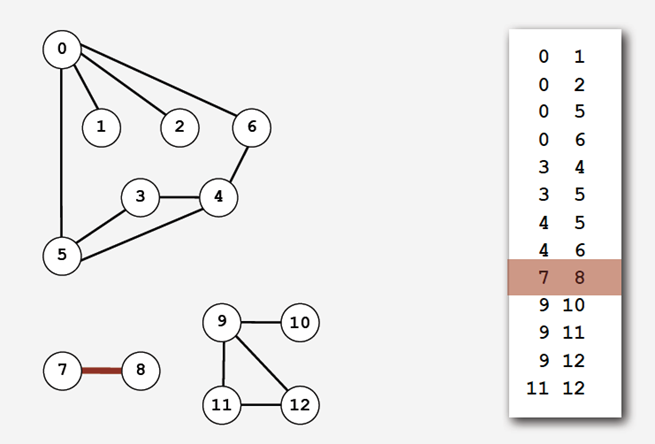
（1）边的集合，如下：

简单但是不满足第二个条件——要实现邻接表adj（）要遍历图中所有的边。

（2）邻接矩阵：

使用一个V乘V的布尔举证，空间上是不满足的。

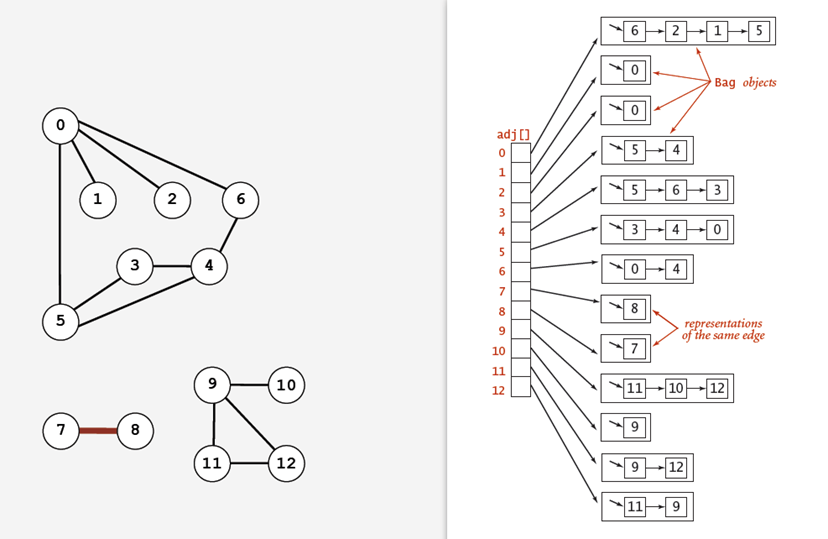
（3）邻接列表：

使用一个顶点为索引的数组列表，其中的每个元素都是和该顶点相邻的顶点列表。

由于采用如上方式具有比较好的灵活性，采用邻接列表来表示的话，可以定义如下数据结构来表示一个Graph对象。

public class Graph
{
    private readonly int verticals;//顶点个数
    private int edges;//边的个数
    private List<int>[] adjacency;//顶点联接列表

    public Graph(int vertical)
    {
        this.verticals = vertical;
        this.edges = 0;
        adjacency=new List<int>[vertical];
        for (int v = 0; v < vertical; v++)
        {
            adjacency[v]=new List<int>();
        }
    }

    public int GetVerticals ()
    {
        return verticals;
    }

    public int GetEdges()
    {
        return edges;
    }

    public void AddEdge(int verticalStart, int verticalEnd)
    {
        adjacency[verticalStart].Add(verticalEnd);
        adjacency[verticalEnd].Add(verticalStart);
        edges++;
    }

    public List<int> GetAdjacency(int vetical)
    {
        return adjacency[vetical];
    }
}

深度优先算法

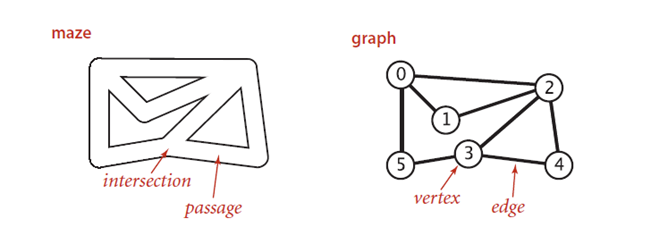
在谈论深度优先算法之前，我们可以先看看迷宫探索问题。下面是一个迷宫和图之间的对应关系：

迷宫中的每一个交会点代表图中的一个顶点，每一条通道对应一个边。

迷宫探索可以采用Trémaux绳索探索法。即：

• 在身后放一个绳子
• 访问到的每一个地方放一个绳索标记访问到的交会点和通道
• 当遇到已经访问过的地方，沿着绳索回退到之前没有访问过的地方：

图示如下：

下面是迷宫探索的一个小动画：

深度优先搜索算法模拟迷宫探索。在实际的图处理算法中，我们通常将图的表示和图的处理逻辑分开来。所以算法的整体设计模式如下：

• 创建一个Graph对象
• 将Graph对象传给图算法处理对象，如一个Paths对象
• 然后查询处理后的结果来获取信息

我们可以看到，递归调用dfs方法，维护了一个marked[]标记数组，在调用之前判断该节点是否已经被访问过。

深度优先算法描述：在访问一个顶点时

1.将它标记为已经访问；

2.递归的访问它的所有没有被标记过的邻居顶点。

public class DepthFirstSearch
{
    private bool[] marked;//记录顶点是否被标记
    private int count;//记录查找次数

    private DepthFirstSearch(Graph g, int v)
    {
        marked = new bool[g.GetVerticals()];
        dfs(g, v);
    }

    private void dfs(Graph g, int v)
    {
        marked[v] = true;
        count++;
        foreach (int vertical in g.GetAdjacency(v))
        {
            if (!marked[vertical])
                dfs(g,vertical);
        }
    }

    public bool IsMarked(int vertical)
    {
        return marked[vertical];
    }

    public int Count()
    {
        return count;
    }
}

试验一个算法最简单的办法是找一个简单的例子来实现。

算法应用：

连通性。给定一幅图，回答“两个给定顶点是否连通？” 或者 “图中有多少个连通子图？”

寻找路径。给定一幅图和一个起点，回答“从s到给定目的顶点v是否存在一条路径？如果有，找出这条路径。”

检测环。给定的图是无环图吗？

双色问题。能够用两种颜色将图的所有顶点着色，使得任意一条边连个顶点的颜色都不相同？这个问题等价于：这是一个二分图吗？

 

深度优先路径查询

有了这个基础，我们可以实现基于深度优先的路径查询，要实现路径查询，我们必须定义一个变量来记录所探索到的路径。

所以在上面的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录，和仅记录从当前节点到起始节点不同，我们记录图中的每一个节点到开始节点的路径。为了完成这一日任务，通过设置edgesTo[w]=v，我们记录从v到w的边，换句话说，v-w是做后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。

注意代码只是在前面算法的基础上维护了一个edgTo数组，并用栈Stack保存路径。

public class DepthFirstPaths
{
    private bool[] marked;//记录是否被dfs访问过
    private int[] edgesTo;//记录最后一个到当前节点的顶点
    private int s;//搜索的起始点

    public DepthFirstPaths(Graph g, int s)
    {
        marked = new bool[g.GetVerticals()];
        edgesTo = new int[g.GetVerticals()];
        this.s = s;
        dfs(g, s);
    }

    private void dfs(Graph g, int v)
    {
        marked[v] = true;
        foreach (int w in g.GetAdjacency(v))
        {
            if (!marked[w])
            {
                edgesTo[w] = v;
                dfs(g,w);
            }
        }
    }

    public bool HasPathTo(int v)
    {
        return marked[v];
    }

    public Stack<int> PathTo(int v)
    {

        if (!HasPathTo(v)) return null;
        Stack<int> path = new Stack<int>();

        for (int x = v; x!=s; x=edgesTo[x])
        {
            path.Push(x);
        }
        path.Push(s);
        return path;
    }
}

 

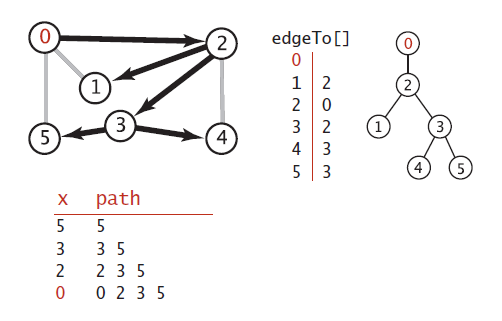
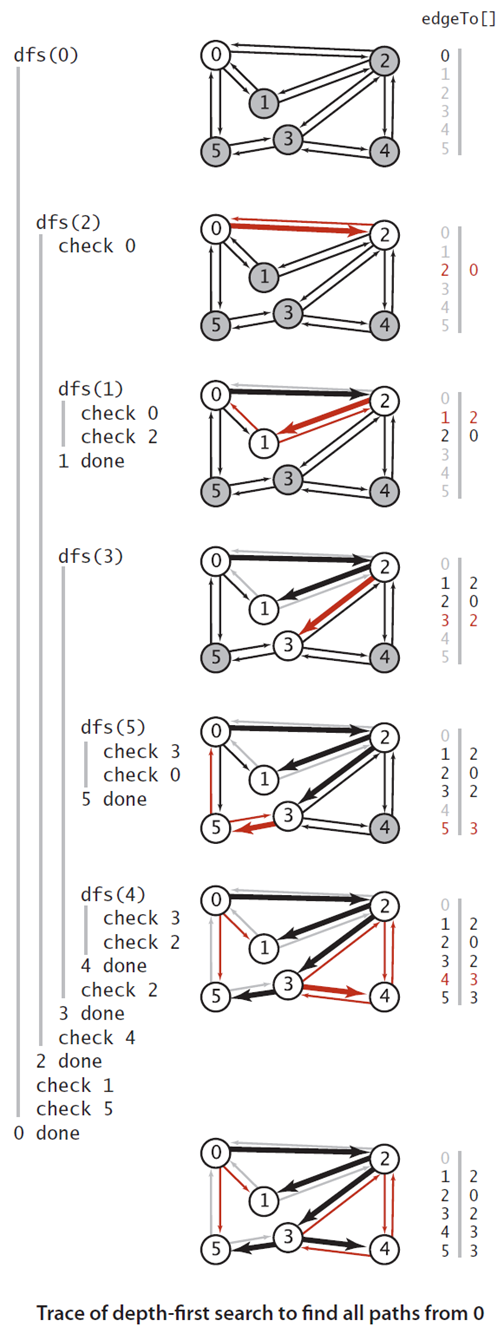
上图中是黑色线条表示 深度优先搜索中，所有定点到原点0的路径， 他是通过edgeTo[]这个变量记录的，可以从右边可以看出，

他其实是一颗树，树根即是原点，每个子节点到树根的路径即是从原点到该子节点的路径。

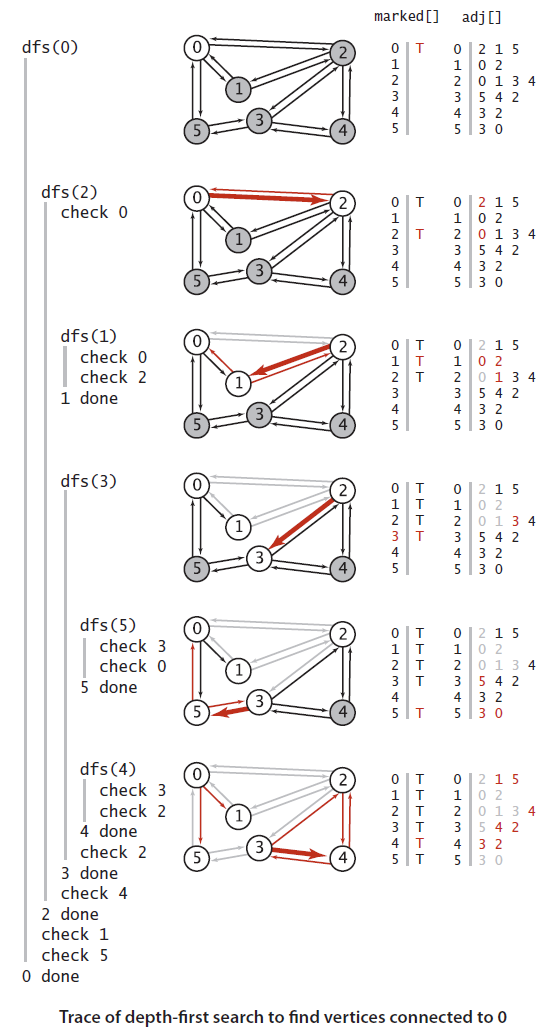
下图是深度优先搜索算法的一个简单例子的追踪。

 

连通分量

API如下：

CC的实现使用了marked[ ]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。递归的深搜第一次调用的参数是顶点0，会标记所有与0连通的顶点。然后构造函数中的for循环会查找每个没有被标记的顶点并递归调用dfs来标记和它相邻的所有顶点。另外，它还使用了一个以顶点作为索引的数组id[ ],将同一个连通分量中的顶点和连通分量的标识符关联起来。这个数组使得connected( )方法的实现变得十分简单。

public class CC {
    private boolean[] marked;
    private int[] id;
    private int count;
    public CC(Graph g){
        marked = new boolean[g.getVertexCount()];
        id = new int[g.getVertexCount()];
        for(int s = 0; s < g.getVertexCount(); s++){
            if(!marked[s]){
                dfs(g,s);
                count++;
            }
        }
    }
    private void dfs(Graph g, int v) {
        marked[v] = true;
        id[v] = count;
        for(int w: g.adj(v))
            if(!marked[w])
                dfs(g,w);
    }
    /** v和w连通吗*/
    public boolean connected(int v, int w)    { return id[v] == id[w]; }
    /** v所在的连通分量的标识符*/
    public int id(int v)    { return id[v]; }
    /** 连通分量数*/
    public int count()        {return count;}

 

检测环

/**
 * 给定的图是无环图吗
 * 检测自环:假设没有自环，没有平行边
 */
public class Cycle {
    private boolean[] marked;
    private boolean hasCycle;
    public Cycle(Graph g){
        marked = new boolean[g.getVertexCount()];
        for(int i = 0;i<g.getVertexCount();i++)
            if(!marked[i])    dfs(g, i, i);
    }
    private void dfs(Graph g, int v, int u) {
        marked[v] = true;
        for(int w: g.adj(v))
            if(!marked[w])    dfs(g, w, v); // 若w没被标记过，那么从w继续递归深搜，把w的父节点作为第二参数
            else if(w != u) hasCycle = true; // 若w被标记过，那么若无环，w必然和父节点相同，否则就是有环
    }
    /** 是否含有环*/
    public boolean hasCycle(){return hasCycle;}

 

双色问题

/**
 * 双色问题：能够用两种颜色将图的所有顶点着色，使得任意一条边上的两个端点的颜色都不同吗？
 * 等价于：判断是否是二分图的问题
 */
public class TwoColor {
    private boolean[] marked;
    private boolean[] color;
    private boolean isColorable;
    public TwoColor(Graph g){
        isColorable = true;
        marked = new boolean[g.getVertexCount()];
        color = new boolean[g.getVertexCount()];
        for(int i = 0; i<g.getVertexCount(); i++)//遍历所有顶点
            if(!marked[i])    dfs(g, i);//没有mark就进行深搜
    }
    private void dfs(Graph g, int v) {
        marked[v] = true;        // 标记
        for(int w: g.adj(v))    // 对邻接表进行遍历
            if(!marked[w]){        // 如果没有被标记
                color[w] = !color[v];    // 当前w节点颜色置为和父节点不同的颜色
                dfs(g, w);                // 对当前节点继续深搜
            }else if(color[w] == color[v]){    // 如果已经被标记，看是否颜色和父节点相同
                isColorable = false;         // 若相同则不是二分图
            }
    }
    /** 是否是二分图*/
    public boolean isBipartite(){return isColorable;}

 

 

广度优先算法

通常我们更关注的是一类单源最短路径的问题，那就是给定一个图和一个源S，是否存在一条从s到给定定点v的路径，如果存在，找出最短的那条(这里最短定义为边的条数最小)

深度优先算法是将未被访问的节点放到一个堆中(stack)，虽然在上面的代码中没有明确在代码中写stack，但是 递归间接的利用递归堆实现了这一原理。

和深度优先算法不同， 广度优先是将所有未被访问的节点放到了队列中。其主要原理是：

先将起点加入队列，然后重复一下步骤直到队列为空：

1.取队列中的下一个顶点V并标记它

2.将与v相邻的所有未被标记过的顶点加入队列

广度优先是以距离递增的方式来搜索路径的。

class BreadthFirstSearch
{
    private bool[] marked;
    private int[] edgeTo;
    private int sourceVetical;//Source vertical

    public BreadthFirstSearch(Graph g, int s)
    {
        marked=new bool[g.GetVerticals()];
        edgeTo=new int[g.GetVerticals()];
        this.sourceVetical = s;
        bfs(g, s);
    }

    private void bfs(Graph g, int s)
    {
        Queue<int> queue = new Queue<int>();
        marked[s] = true;
        queue.Enqueue(s);
        while (queue.Count()!=0)
        {
            int v = queue.Dequeue();
            foreach (int w in g.GetAdjacency(v))
            {
                if (!marked[w])
                {
                    edgeTo[w] = v;
                    marked[w] = true;
                    queue.Enqueue(w);
                }
            }
        }
    }

    public bool HasPathTo(int v)
    {
        return marked[v];
    }

    public Stack<int> PathTo(int v)
    {
        if (!HasPathTo(v)) return null;

        Stack<int> path = new Stack<int>();
        for (int x = v; x!=sourceVetical; x=edgeTo[x])
        {
            path.Push(x);
        }
        path.Push(sourceVetical);
        return path;
    }

}

算法应用：最短路径问题

 

总结：

深度优先搜索和广度优先搜索都是将起点存入数据结构中，然后重复一下步骤直到数据结构被清空：

1.取其中的下一个顶点并标记它

2.将v的所有相邻而未被标记的顶点加入数据结构

这两个算法 的不同之处仅在于从数据结构中获取下一个顶点的规则（广度优先来说是最早加入的顶点，对于深度优先搜索来说是最晚加入的顶点）。