我们希望并期望我们的网络能够从他们的错误中学习的很快,首先看一个小例子。
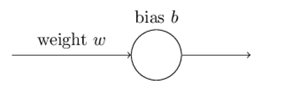
我们将训练这个神经元做一些非常简单的事情:把输入的1转换成输出的0。当然,如果我们不是用学习算法,可以很容易地计算出一个适当的权重w和偏差b。但是我们为了说明一些问题,就使用梯度下降法来学习权重和偏差,这对于后面的学习很有启发性。让我们来看看神经元是如何学习的。
我们将训练这个神经元做一些非常简单的事情:把输入的1转换成输出的0。当然,如果我们不是用学习算法,可以很容易地计算出一个适当的权重w和偏差b。但是我们为了说明一些问题,就使用梯度下降法来学习权重和偏差,这对于后面的学习很有启发性。让我们来看看神经元是如何学习的。
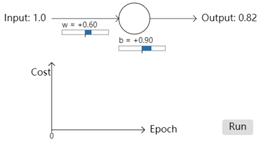
首先我们设置开始学习的一些初始值,初始权重w为0.6,b为0.9,学习率(步长)为0.15,这些值的选择并没有什么特殊之处。当输入值为1时,神经元的初始输出是0.82,这个值和我们期望的0之间有很大差距,所以在我们的神经元接近期望的输出之前,需要相当多的学习。因此我们利用梯度更新权重和偏差。最终获得下面的结果,300次的epoch之后,输出为0.09。虽然不是我们期望的0,但是已经算是一个不错的结果了。
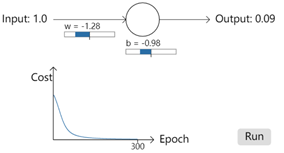
再一次实验,这次将权重和偏差设置为2.0,再次运行结果发现,经过300次epoch之后,输出为0.2,这个结果和0之间差距还是比较大的。同样是300次epoch,但是结果却差距很大。而且看下图,前面大约150次epoch,cost的下降是非常非常的慢,也就是学习速度很慢。那么这是什么原因导致的呢?
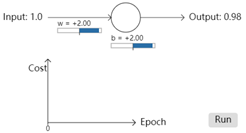
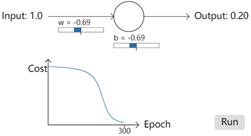
经过初步查看,可以简单了解到,当期望输出和真实值之间差距比较远时训练速度要比差距近时快。
1、为什么w=0.6,b=0.9时,学习速度很快,而w=2.0,b=2.0时,学习速度就很慢,那么导致速度慢的原因到底是啥?
我们一步一步分析:
首先,神经元的学习是通过偏导数改变权值和偏差,改变的速度由和决定。因此,所谓的学习慢也就是偏导数比较小。那么我们来计算一下这里的偏导数。
这里的损失函数为二次损失函数(quadratic cost function),如公式(54)。

a为期望的输出,为了更方便的表示,让a = σ(z),z=ωx=b,用链式法则求出权重和偏移量的偏导数,如下:

故:
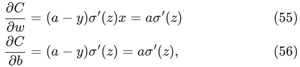
这儿x=1,y=0带入可简化为后面的式子。这样,我们把关注点放在σ'(z)上面。σ(z)是激活函数,该激活函数为sigmoid函数,图像如下:
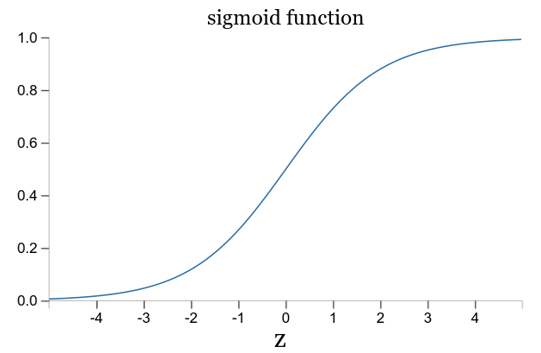
从上面这幅图片可以看出,当神经元的输出接近1时,函数的波形非常的平缓,σ'(z)很小,根据公式(55)和公式(56)得知很小就意味着∂C/∂ω很小,也就是偏导数很小。梯度下降的就慢,自然会导致学习很慢。更重要的是这种情况不仅仅发生在上面的简单的例子中,实际应用中也经常遇到。
那如何避免学习速度慢的情况?Cross-entropy是凭空出来的吗?
通过前面的分析我们知道由于σ'(z)的存在,可能出现学习速度很慢的情况,有研究者就开始思考,既然σ'(z)对速度有影响,那能不能把σ'(z)去掉呢?
思考公式(55)和(56),如果去掉σ'(z),公式变成如下形式:
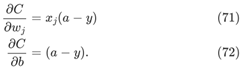
如果选择一个代价函数使得该式子成立,那么当神经元的实际输出a和期望输出y之间差距越大,偏导数就越大,梯度下降就越快,学习速度也越大。研究者们以一种简单的方式捕捉到一种直觉,即初始误差越大,神经元学习的速度就越快,就消除了学习速度下降的问题。
由前面的链式法则
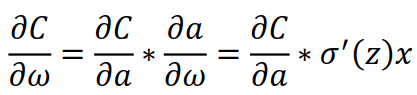
σ(z)为sigmod函数,σ'(z) = σ(z)(1-σ'(z)) = a(1-a),上式就变成
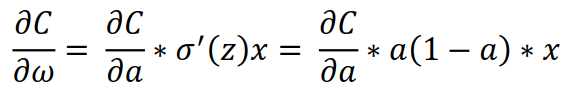
注:sigmoid函数求导过程https://www.cnblogs.com/xhslovecx/p/10817889.html
结合公式(71),暂时只考虑一个输入,j=1。
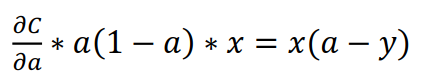

对(75)求原函数
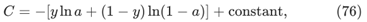
这是单个训练示例对代价函数的贡献。为了得到完整的代价函数,需要对训练实例进行平均,得到
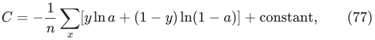
这里的常数是每个训练例子中单个常数的平均值。
(77)就是cross-entropy损失函数的基本形式。因此cross-entropy并不是凭空产生的,它是用一种简单而自然的方式发现的东西。
3、为什么cross-entropy可以作为损失函数?
那么思考,通过上面的方式获得的方程C,是否真的可以作为损失函数?
公式(77)的两个属性使得cross-entropy可以作为损失函数。
其一:它是非负数,C>0;由于y和a均位于0~1之间,因此C的第一项ylna和第二项(1-y)ln(1-a)均为负数,乘上前面的负号,整个式子为非负数。
其二:如果神经元的实际输出接近所有训练输入的期望输出,则交叉熵将接近于零;如果y=0,
则
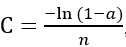
,a约等于0时,ln(1-a)约等于ln(1) = 0, C约等于0。同理,当y=1时,C=-lna/n, a约等于1,C约等于0。
因此,cross-entropy可以作为损失函数。
利用cross-entropy作为损失函数实现上面简单的例子,

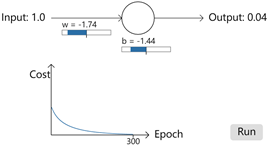


正如我们所希望的那样, 这次神经元学得很快。仔细观察,会发现Cost曲线的斜率最初比quadraticsun损失函数曲线上的初始平坦区域陡得多。这就是交叉熵给我们带来的陡度,也就是当神经元出现严重错误的时候,cross-entropy会以相当快的速度学习。 跟quadraticsun损失w和b为2.0时相比较,cross-entropy简直太优秀。
Cross-entropy代价函数是否完全可以替代quadratic代价函数,如果为否,则分别适用于什么场合?
当激活函数为sigmoid时,cross-entropy往往是较好的选择。实际使用过程中,权重和偏差往往是随机设定的,这样很有可能带来学习缓慢的情况。
当输出层为线性神经元时,采用quadratic损失可能是一个更好的选择。假设最后一层的神经元都为线性神经元,则sigmoid函数就不被应用了。输出就变为a=z,而不是a=σ(z)。