题面
http://acm.hdu.edu.cn/showproblem.php?pid=6637
题解
前置知识
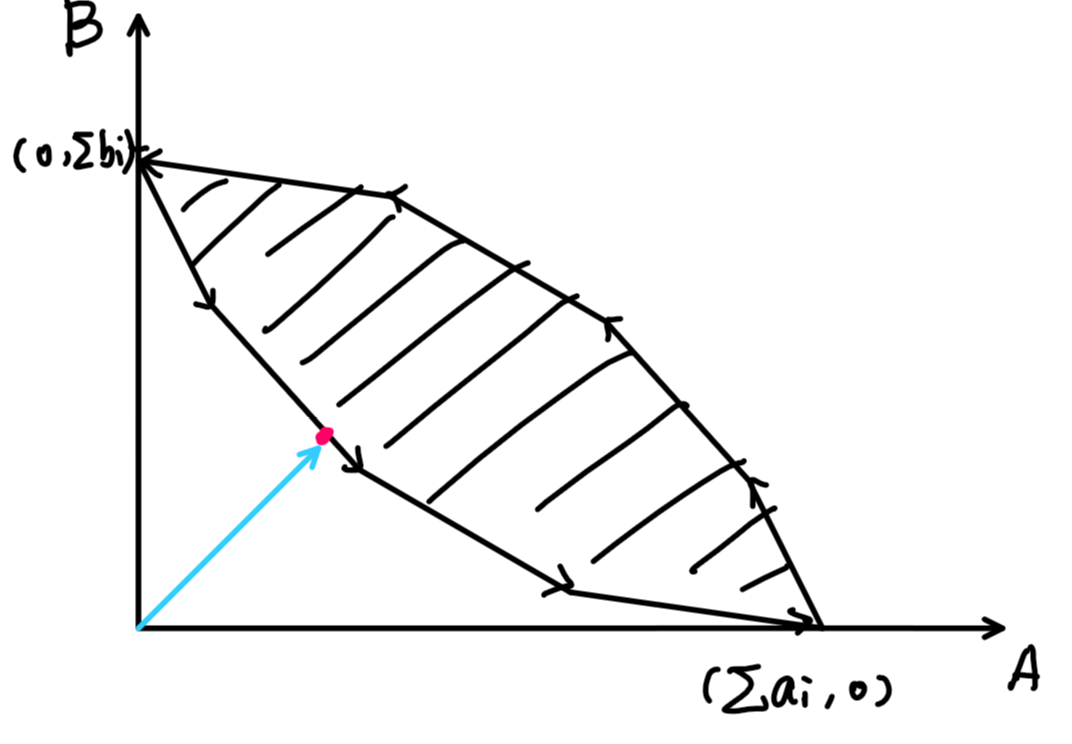
题目中的(a_ix_i)与(b_i(1-x_i))容易让人想到定比分点公式。考虑建立一个平面直角坐标系,横轴为A轴,纵轴为B轴。那么,第i个任务可以视为一条从((0,b_i))到((a_i,0))的线段,这条线段上、距离左端点为全长(x)倍的点((x{in}[0,1])),其坐标正好为((a_ix,b_i(1-x)))。
所以,初始时可置((X,Y)=(0,0))。对于第i个任务,可以视作从((0,b_i))到((a_i,0))的线段上,选取某一点,然后把这一点所对应的向量加入((X,Y))。求最终(max(X,Y))的最小值。
发现对于第k个询问,即加入了前k条线段后,所有可能的((X,Y))构成的点集即为前k条线段所构成的闵可夫斯基和。线段的凸包仅由两条互反的有向线段组成,所以运用归纳法,结合凸形闵和的性质,可以证明前k条线段构成的闵和是一个中心对称图形。

然后这个图形中,横纵坐标最大值最小的点就是直线(A-B=0)与此图形的第一个交点。
发现凸包的上半部分没什么用,所以只考虑下半部分。
考虑用数据结构维护,每次要做的就是插入一条线段:按极角为关键字找到插入的位置,把左边的所有线段向上平移(b_i),右边的所有线段向右平移(a_i)。

- 如图,黑色为原凸包,插入一条橙色线段,粉色+橙色为新凸包
查询交点时,由于这里的所有线段的极角都在((-{frac{pi}{2},0}))之间,所以这里所有线段的起始点的“横坐标-纵坐标”值也是有序的,按此为关键字,查找0的前驱即可。
可以使用平衡树维护,时间复杂度(O({sum}nlog n))。
- P.S.由于是在学习计算几何期间做的此题,所以用了闵和的方法;但是此题有非计算几何的做法,详见https://blog.csdn.net/ehdhg13455/article/details/98966356
代码
//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
#define rg register
#define In inline
#define N 250000
#define inf 0x3f3f3f3f3f3f3f3f
In ll read(){
ll s = 0,ww = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')ww = -1;ch = getchar();}
while('0' <= ch && ch <= '9'){s = 10 * s + ch - '0';ch = getchar();}
return s * ww;
}
In ll write(ll x){
if(x < 0)x = -x,putchar('-');
if(x > 9)write(x / 10);
putchar('0' + x % 10);
}
In ll gcd(ll a,ll b){
return b ? gcd(b,a % b) : a;
}
struct vec{
ll x,y;
vec(){}
vec(ll _x,ll _y){x = _x,y = _y;}
In friend vec operator + (vec a,vec b){
return vec(a.x + b.x,a.y + b.y);
}
In friend vec operator - (vec a,vec b){
return vec(a.x - b.x,a.y - b.y);
}
In friend ll Dot(vec a,vec b){
return a.x * b.x + a.y * b.y;
}
In friend ll Cross(vec a,vec b){
return a.x * b.y - a.y * b.x;
}
};
struct line{
vec p,v;
line(){}
line(vec _p,vec _v){p = _p,v = _v;}
In friend void printits(line a){ //输出直线a与直线x=y的交点的横坐标
ll x = Cross(vec() - a.p,a.v),y = Cross(a.v,vec(1,1));
ll d = gcd(x,y);
write(x / d),putchar('/'),write(y / d),putchar('
');
}
};
ll a[N+5],b[N+5];
struct Splay{
ll rt,cnt;
ll fa[N+5],c[N+5][2],id[N+5];
vec flag[N+5],p[N+5];
void clear(){
rt = cnt = 0;
}
In void reset(int u,int f,int i){
c[u][0] = c[u][1] = 0;
flag[u] = vec();
fa[u] = f;
id[u] = i;
}
In void pushdown(int u){
if(!flag[u].x && !flag[u].y)return;
if(c[u][0])p[c[u][0]] = flag[u] + p[c[u][0]],flag[c[u][0]] = flag[c[u][0]] + flag[u];
if(c[u][1])p[c[u][1]] = flag[u] + p[c[u][1]],flag[c[u][1]] = flag[c[u][1]] + flag[u];
flag[u] = vec();
}
void rotate(int u){
int f = fa[u],g = fa[f],k = c[f][1] == u,w = c[u][!k];
if(g)c[g][c[g][1]==f] = u;
fa[f] = u;
c[f][k] = w;
fa[u] = g;
c[u][!k] = f;
if(w)fa[w] = f;
}
void splay(int u,int goal){
while(fa[u] != goal){
int f = fa[u],g = fa[f];
if(g != goal){
if((c[f][1]==u) ^ (c[g][1]==f))rotate(u);else rotate(f);
}
rotate(u);
}
if(!goal)rt = u;
}
void insert(int i){
if(!rt){
rt = ++cnt;
reset(cnt,0,i);
return;
}
int u = rt,v;bool k;
while(1){
pushdown(u);
v = c[u][k=(Cross(vec(a[i],-b[i]),vec(a[id[u]],-b[id[u]]))<=0)];
if(!v)break;
u = v;
}
c[u][k] = ++cnt;
reset(cnt,u,i);
splay(cnt,0);
}
void pro(){
pushdown(rt);
int lc = c[rt][0],rc = c[rt][1];
flag[rc] = flag[rc] + vec(a[id[rt]],0); p[rc] = p[rc] + vec(a[id[rt]],0);
flag[lc] = flag[lc] + vec(0,b[id[rt]]); p[lc] = p[lc] + vec(0,b[id[rt]]);
pushdown(rt);
int u = c[rt][1]; //u:根结点rt的后缀
while(c[u][0])pushdown(u),u = c[u][0];
p[rt] = p[u] + vec(-a[id[rt]],b[id[rt]]);
}
line pred(){ //寻找并输出p.x<p.y的最后一个结点
ll ans = 1,maxn = -inf;
ll i = rt;
while(i){
pushdown(i);
if(p[i].x < p[i].y){
if(p[i].x - p[i].y > maxn)maxn = p[i].x - p[i].y,ans = i;
i = c[i][1];
}
else i = c[i][0];
}
return line(p[ans],vec(a[id[ans]],-b[id[ans]]));
}
}S;
int main(){
// freopen("H6637.in","r",stdin);
// freopen("H6637.out","w",stdout);
ll T = read();
while(T--){
ll n = read();
S.clear();
a[0] = 0,b[0] = 1,a[n+1] = 1,b[n+1] = 0;
S.insert(0);S.p[S.cnt] = vec(0,1); //
S.insert(n + 1);S.p[S.cnt] = vec(0,0); //第一和第二号节点,用来防止溢出
for(rg int i = 1;i <= n;i++){
a[i] = read(),b[i] = read();
S.insert(i);
S.pro();
printits(S.pred());
}
}
return 0;
}