1,相关概念
路径长度,从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称做路径长度。
树的路径长度就是从树根到每一结点的路径长度之和。
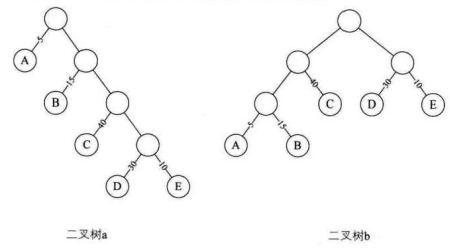
二叉树a的树路径长度就为1+1+2+2+3+3+4+4=20 。二叉树b的树路径长度就为 1+2+3+3+2+1+2+2=16 。
结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。
树的带权路径长度为树中所有叶子结点的带权路径长度之和 。
带权路径长度 WPL 最小的二叉树称做赫夫曼树。
二叉树 a 的 WPL=5*1+15*2+40*3+30*4+10*4=315
二叉树 b 的 WPL=5*3+15 *3+40*2+30*2+10*2=220
2,赫夫曼树的构造
1.先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列,即:A5,E10 , B15 , D30 , C40。
2.取头两个最小权值的结点作为一个新节点N1的两个子结点,注意相对较小的是左孩子,这里就是A为N1的左孩子,E为N1的右孩子,如图 6-12-5 所示。新结点的权值为两个叶子权值的和 5+10=15 。
3.将N1替换A与E,插入有序序列中,保持从小到大排列。即 : N115 , B15 ,D30, C40。4
4.重复步骤2,将N1与B作为一个新节点N2的两个子结点。如图 6-12-6 所示。N2的权值=15+15=30。
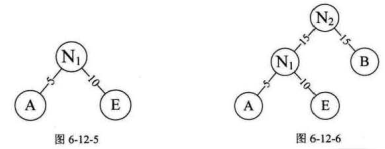
5.将N2替换N1与B,插入有序序列中,保持从小到大排列。即: N2 30 , D30 ,C40。
6.重复步骤2。将N2与D作为一个新节点N3的两个子结点。如图6-12-7所示。N3的权值=30+30=60 。
7.将N3替换N2与D,插入有序序列中,保持从小到大排列。即:C40 , N3 60。
8.重复步骤2。将C与N3作为一个新节点T的两个子结点,如图6-12-8所示。由于T即是根结点,完成赫夫曼树的构造。
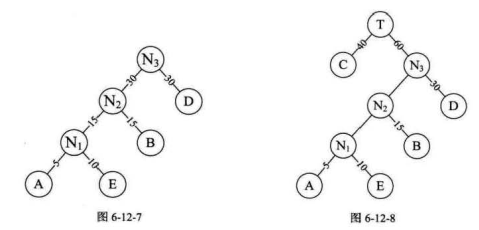
此时的图6-12-8二叉树的带权路径长度WPL=40*1+30*2+15*3+10*4+5*4=205
3,赫夫曼编码
赫夫曼研究这种最优树的目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题(数据压缩)。
假设我们需要传输的六个字母的出现频率为A 27, B 8, C 15 , D 15 , E 30, F 5,合起来正好是100%。 我们进行赫夫曼编码。
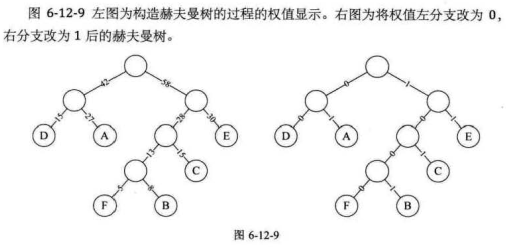

一般地,设需要编码的字符集为{d1,d2,…,dn },各个字符在电文中出现的次数或频率集合为{ W1,W2,…,Wn},以d1,d2,…,dn作为叶子结点,以W1,W2,…,Wn作为相应叶子结点的权值来构造一棵赫夫曼树。规定赫夫曼树的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,这就是赫夫曼编码。